自动驾驶路径跟踪控制——驾驶员预瞄模型

1. 驾驶员预瞄控制概述

    近年来随着智能汽车的发展，出现了很多关于汽车运动的控制算法，包括方向控制算法、速度控制算法以及方向与速度综合控制算法。
    虽然这些算法大多不以驾驶员模型命名，但实质上它们无一例外地描述了驾驶员对汽车运动的某种控制行为，从广义上来说这些控制算法从属于驾驶员模型。

1.1 第一个得到应用的驾驶员模型(Crossover模型)

    国际上最早得到应用的驾驶员模型大概是McTure等人提出的Crossover模型，这是一种补偿跟踪模型。其系统框图如图所示，其中H(s)表示驾驶员的控制特性，G(s)表示汽车的动力学特性。Crossover 模型特点
     具有结构简单并且参数可以通过理论方法确定的优点。
Crossover 模型应用
     应用于预测人-车闭环系统抵抗侧风等外界干扰的稳定性相关研究。

1.2 预瞄概念的诞生

     Kondo提出了线性预估模型。该模型规定驾驶员总是提前一段距离$L_p$预瞄预期轨迹，并假定无转向盘输入时汽车将沿当前车体坐标系的纵轴 $X_V$ 方向行驶，而驾驶员对方向盘的理想操作量与预期轨迹点在车体坐标系下的横向位移偏差 $\epsilon$ 成正比。线性预估模型特点
     虽然该模型在预估环节存在较大偏差，模型参数也无法通过理论方法确定，但该模型描述了驾驶员的前视特点，比补偿跟踪模型更符合真实驾驶员的行为特性.
线性预估模型意义
     预瞄的概念由此诞生，并对后来驾驶员模型的发展产生了深远的影响

1.3 驾驶员模型环节

    按照车辆的运动特性，轨迹跟踪可分为纵向跟踪与横向跟踪。想要实现一个优秀的路径跟踪一个很重要的办法就是使车辆如同被优秀的驾驶员控制一般运行。（Apollo的控制策略为纵向PID，横向LQR）
    因为一个算法是否足够优越最后也是由人来评价的，车辆是否偏离路径，是否可以抵抗干扰，是否可以应对突发情况都是一个优秀的驾驶员应该做到的。
    因此研究驾驶员模型也是研究路径跟踪的核心问题之一，同时也在同时在“人一车一路”闭环系统研究中发挥重要作用。
    与室内机器人的一般控制方法（需要得到实时的状态信息予以控制）不同，汽车通常是高速运动的。汽车的高速运动特性也决定了控制汽车运动的频率比较低，否则容易导致震荡。
    根据驾驶员的前视作用，真实驾驶员的驾驶活动可假想得划分为三个环节： 信息感知环节、轨迹决策环节和校正操作环节。
    通过建立精准的驾驶员模型，提高自动驾驶汽车对道路自适应性以及高速工况下控制精度和平顺性，成为现阶段自动驾驶汽车轨迹跟踪的关键。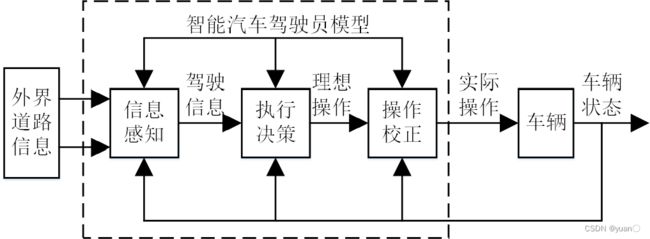

ps：现在的驾驶员模型主要着手于执行决策与操作矫正

---

    早期研究最多的便是驾驶员横向控制模型，因为相对于纵向跟踪控制而言，横向跟踪控制的发展相对较为不成熟。
    因为车辆是一个非线性系统，存在强耦合、参数不确定性等控制难题。因此，对于车辆这样复杂的系统，横向路径跟踪控制一直是汽车控制领域的研究热点。
    自上世纪中期以来各国学者便提出了许多基于汽车方向控制的驾驶员模型，其中可以分为补偿跟踪模型与预瞄跟踪模型。

1.4 补偿跟踪模型

    补偿跟踪模型提出时间最早，其代表为PID模型与Crossover模型。
    驾驶员补偿跟踪模型输入为当前时刻预期轨迹的信息（一般为侧向偏差）和汽车行驶的状态信息（一般为汽车的侧向位置）之间的偏差，输出为方向盘转角。
    但会导致方向盘操控频繁，引起震荡（控制频率太高），且不适用于高速行驶时的预瞄跟踪运动。

1.5 预瞄跟踪模型

    预瞄跟踪模型通过输入道路路径，在车辆前方设置预瞄点模拟驾驶员开车视线情况分析预瞄点与路径的相对状态，结合车辆目前的行驶姿态，从而输出方向盘转角。
    其中$f$代表输入的预期轨迹，$f_e$表示预瞄环节估计的汽车未来时刻的位置状态$\epsilon$表示估计值偏差$\delta$表示输入汽车的方向盘转角，$y$表示实际输出车辆轨迹，$P(S)$，$F(S)$，$B(S)$分别代表预瞄环节，前向校正环节与反馈估计环节。

1.6 速度控制模型

    速度控制模型通常用于巡航控制研究中，下面就介绍几个速度控制驾驶员模型。

1.6.1 速度控制的驾驶员模型

    日本学者K.Yoshimoto提出了一个速度控制的驾驶员模型。
    该模型以当前汽车和前方障碍的相对距离和此刻驾驶员所感知的汽车纵向加速度为基础，经过一个匀减速过程，来预测汽车在停止前和前面障碍之间的距离。
    驾驶员设定一个汽车和前方障碍之间的安全距离，然后驾驶员根据此安全距离和上面得到的预测距离之间的差值来决定制动踏板的控制命令。

1.6.2 驾驶员最优预瞄纵向加速度模型

    吉林大学高振海等人基于预瞄跟随理论和模糊决策理论建立了一种驾驶员最优预瞄纵向加速度模型。

    模型中考虑了驾驶员滞后特性和汽车动力学系统非线性特性的因素，并通过控制油门和制动踏板来控制汽车车速变化，能够较好的反映驾驶员对车速的控制行为。

1.7 总结

    大多数现有模型仍属于跟随既定轨迹或既定速度曲线的跟随控制模型，只有少数模型具有实时决策预期轨迹的功能。
    根据决策时所采用的优化变量不同，具有轨迹决策功能的模型又可分为两种，其中，大多数模型直接以驾驶操作量作为优化变量，而最优预瞄加速度模型与其他模型不同，优化变量采用中间变量——预瞄加速度。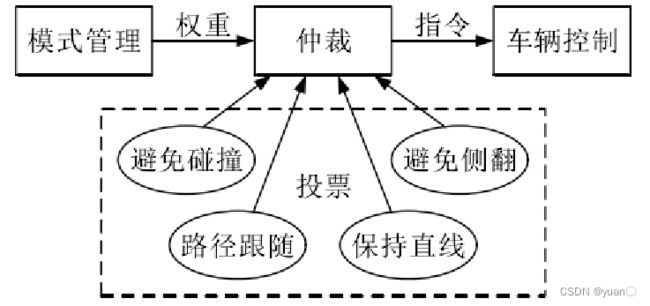

2. 驾驶员模型

2.1 预瞄策略（单点预瞄和区段预瞄）

     一般来说，预瞄策略取决于预瞄时间的长度，以及预瞄窗的宽度和形式，随着预瞄窗宽度和形式的变化，可以衍生出多种不同的预瞄策略。     研究经验表明，就预瞄策略对人-车闭环系统跟随性能的影响而言，预瞄时间是主要因素，而预瞄窗的宽度和形式只是次要因素。而且，单点预瞄时的跟随性能通常比区段预瞄时更好。（区段预瞄有可能会产生积分抵消，无法正确作出判断）。

2.2 预瞄最优曲率模型(位置预瞄模型)

    在车速很低的情况下几乎不涉及汽车的动态响应问题，汽车的运动简单的服从于“阿克曼几何关系”即汽车轨迹曲率与方向盘转角成正比（类似于上一讲中的纯追踪模型）。
    依据此关系，可以列出下式：$$\frac{1}{R}=\frac{{\delta }_{SW}}{iL}$$$$\ddot{y}=\frac{v^2}{R}=\frac{{\delta }_{SW}\cdot v^2}{iL}$$式中：${\delta }_{SW}$——方向盘转角
      $L$——轴距
      $y$——汽车的横向位置
      $\ddot{y}$——汽车的横向加速度（向心加速度）
      $v$——车速
      $i$——转向系传动比
      $R$——汽车转弯半径
    我们考虑汽车在一个预定的路线上行驶，轨道中心的方程为$f(t)$,设在$t_0$时刻，汽车的状态为$y=y(t_0)$$\&\&$$\dot{y}=\dot{y}(t_0)$ [在程序中，一般以差分的形式代替微分$\frac{f(t+\Delta t)-f(t)}{\Delta t}$] 驾驶员向前预视一个距离$d$，相应的可以算出前视时间为$T=\frac{d}{v}$ ,驾驶员前视点的坐标为$f(t_0+T)$,此时选择一个方向盘角度${\delta }_{SW}$ ，对应着汽车的轨迹曲率为 $\frac{1}{R}$ ，横向加速度为 $\ddot{y}(t)$ ,这样经过时间$T$之后，在$t_0+T$处的位置为$y(t_0+T)$，对其在$t=t_0$处泰勒展开，取前三项，得：$$y(t_0+T)=y(t_0)+T\dot{y}(t_0)+\frac{T^2}{2}\ddot{y}(t_0)$$

ps：图中的y(t)应为y(t0),t+T应为t0+T,且该图忽略了泰勒展开的二阶项

    在此例中，我们先假设驾驶员的目光集中于前方一点处，即为单点预瞄。
    根据“最小误差原则”，驾驶员总是希望选择一个最优的轨迹曲率 $1/R$,使得汽车走过距离$d$之后，其横向位置$y(t_0+T)$与预期的轨道坐标$f(t_0+T)$一致。
    联立下式，$$\begin{array}{c}y(t_0+T)=y(t_0)+T\dot{y}(t_0)+\frac{T^2}{2}\ddot{y}(t_0)\\ \ddot{y}(t)=\frac{v^2}{R}\\ d=vT\\ f(t_0+T)=y(t_0+T)\end{array}$$    得最优的轨迹曲率 $1/R$$$\frac{1}{R}=\frac{2}{d^2}\left[f(t_0+T)-y(t_0)-T\dot{y}(t_0)\right]$$    或最优加速度为：
$$\ddot{y}(t_0)=\frac{2}{T^2}\left[f(t_0+T)-y(t_0)-T\dot{y}(t_0)\right]$$    由式子：
$$\frac{1}{R}=\frac{{\delta }_{SW}}{iL}$$$$\ddot{y}=\frac{v^2}{R}=\frac{{\delta }_{SW}\cdot v^2}{iL}$$    得最优转角关系：$${\delta }_{SW}=\frac{2iL}{d^2}\left[f(t_0+T)-y(t_0)-T\dot{y}(t_0)\right]$$

2.3 最优预瞄侧向加速度模型

2.3.1 最优预瞄侧向加速度决策假说

    最优预瞄侧向加速度决策假说，将驾驶员控制汽车行驶的行为划分成以下两个阶段：
    首先，根据前方预期轨迹和当前时刻的汽车运动状态，通过某种预瞄策略决策得到一个最优预瞄侧向加速度；
    然后，对汽车的侧向动力学特性以及驾驶员本身的反应延迟和动作之后滞后特性进行校正，得到一个最优的转向盘操作指令。
     随着时间推移不断重复上述预瞄和校正过程，便可控制汽车跟随驾驶与预期的轨迹行驶，体现了预测控制理论的滚动优化思想。
     在实际的驾驶过程中，驾驶员观测前方道路的视角，总是随着汽车运动而不断发生变化。
    因此，在对驾驶员控制行为进行建模时，预瞄坐标系$x-o-y$的方向要始终与车体坐标系 $xv-ov-yv$ 保持一致。
     在未来一段时间内，如果保持侧向加速度为 0，则汽车将沿当前时刻的速度方向做直线运动；
     如果驾驶员通过预瞄提前判断出汽车沿该直线方向运动一段时间之后将会偏离预期轨迹，那么他（或她）就会期望汽车能够产生一定的侧向加速度以弥补这种偏差，该侧向加速度即为最优预瞄侧向加速度。

2.3.2 最优预瞄侧向加速度决策算法

     $T_P$为预瞄时间，$x(t)$ 和$y(t)$ 分别为当前时刻汽车质心位置在预瞄坐标系中的$x$ 坐标和 $y$ 坐标；$f(t)$为当前时刻汽车质心位置对应预期轨迹的 $y$ 坐标；$V$ 为当前时刻的汽车运动速度矢量；$\dot{x}(t)$ 和 $\dot{y}(t)$分别为 $V$ 的 $x$ 方向上的分量和 $y$ 方向上的分量； $f(t+T_p)$ 为驾驶员所预期的在未来$t+T_p$时刻汽车质心到达位置的 $y$ 坐标，该位置是前方预期轨迹上的一点； $\ddot{y}(t)$ 即为最优预瞄侧向加速度。

2.3.3 位置加方位预瞄模型

     在决策最优预瞄侧向加速度时，假定了侧向加速度在整个预瞄时间段内保持不变，即按照时间$t$ 的二次函数来预测汽车的未来行驶轨迹：$$y(t+T_p)=y(t)+T_p\dot{y}(t)+\frac{{T_p}^2}{2}\ddot{y}(t)$$      如果驾驶员期望未来到达位置的$y$坐标为 $f(t+T_p)$ ，根据上式，则最优预瞄侧向加速度可由下式求得：$$f(t+T_p)=y(t)+T_p\dot{y}(t)+\frac{{T_p}^2}{2}\ddot{y}(t)$$    在上式中，只有$\ddot{y}(t)$ 一个未知数，因此由上式假设求得的最优预瞄侧向加速度能满足上式所设的位置条件，而无法兼顾汽车行驶轨迹与驾驶员预期轨迹方位的一致性。
     若要在满足位置条件的同时兼顾方位的一致性，则至少要按照时间$t$ 的三次函数来预测汽车的未来行驶轨迹：$$y(t+T_p)=y(t)+T_p\dot{y}(t)+\frac{{T_p}^2}{2}\ddot{y}(t)+\frac{\lambda {T_p}^3}{6}{y}^{(3)}(t)$$     式中，$\lambda$ 为方位作用系数，用于松弛驾驶员对方位跟随的要求，在[0,1]取值。
    对上式求导，丢掉四阶项，可得：     $$\dot{y}(t+T_p)=\dot{y}(t)+T_p\ddot{y}(t)+\frac{{T_p}^2}{2}{y}^{(3)}(t)$$    同时满足位置条件和方位条件的$\ddot{y}(t)$ 和 $y^{(3)}(t)$ ,可由以下两式求得$$f(t+T_p)=y(t)+T_p\dot{y}(t)+\frac{{T_p}^2}{2}\ddot{y}(t)+\frac{\lambda {T_p}^3}{6}{y}^{(3)}(t)$$$$\dot{f}(t+T_p)=\dot{y}(t)+T_p\ddot{y}(t)+\frac{{T_p}^2}{2}{y}^{(3)}(t)$$    式中， $\dot{f}(t+T_p)$代表了预期轨迹的方位信息(预期轨迹曲线的斜率)。
    由上述两式消去$y^{(3)}(t)$ ，可得：$$f(t+T_p)-\frac{\lambda T_p}{3}\dot{f}(t+T_p)=y(t)+(1-\frac{\lambda }{3})T_p\dot{y}(t)+(\frac{1}{2}-\frac{\lambda }{3}){T_p}^2\ddot{y}(t)$$    顾及上式，同时由位置条件和方位条件求解$\ddot{y}(t)$ 的过程，称为位置加方位预瞄的最优预瞄侧向加速度策略。
    研究经验表明，通过适当设置方位作用系数$\lambda$ ，$PO$ 预瞄模型不仅可以有效提高人-车闭环系统的跟随性能，而且描述了位置预瞄模型无法描述的如下实际现象：
    在汽车进入弯道之前，为顺利通过弯道，驾驶员通常会先向反方向转动转向盘。
    综上所述，$PO$ 预瞄模型在位置预瞄模型基础上兼顾了汽车行驶轨迹与驾驶员预期轨迹方位的一致性，是一种更为完善的驾驶员方向控制模型。

2.3.4 方向与速度综合控制的驾驶员模型

    它与方向控制模型相比具有两个显著特点：

• 根据当前汽车运动状态和交通环境信息实时决策预期轨迹；
• 对汽车行驶的方向与速度进行综合控制。

    方向与速度综合控制模型，将驾驶员对汽车运动的控制行为划分成信息感知、预瞄决策和校正操作三个部分。

3. 双点预描控制模型

3.1 驾驶员视觉注意机制

    人类生理、心理学家Land和Horwood于1994年对人类驾驶员在弯道行驶时的行为进行研究。
    研究发现，在驾驶车辆时大部分驾驶员的视觉范围都局限在很小的范围内，驾驶员注意的范围主要包括“远”“近”两个区域。     远近预瞄点代表着两个预瞄距离不同的预瞄点，也就是预瞄时间较长与较短的两个点。
    郭孔辉院士已经验证较长的预瞄时间可以使驾驶过程更加平稳，方向盘的摆动幅度较小，但车辆会与期望路径产生较大偏差。
    采用较小的预瞄时间则可以提高车辆与期望路径的追随性能，但会使方向盘的转动更加剧烈，使车体产生震荡，相比较长的预瞄时间更容易出现失稳现象。所以选择较远点与选择较近点都不是最理想的选择。
    因此前方道路整体信息是很关键的信息，而不能局限于一点上，对此郭孔辉院士提出了${\tau }^2$预瞄窗的概念。
    ${\tau }^2$预瞄窗的概念，即将前方预瞄距离从$d_1$到$d_2$一段道路的横向偏差进行积分，将积分结果作为输入。

    这种输入可以将一段道路的信息纳入考虑，既考虑了远点信息，又兼顾了近点信息，但却可能出现‘信息混淆’的现象。
    对于下图两种不同情况，可是驾驶员得到的道路输入值完全相同，导致不正确的输出。

    所以采用远近两个预瞄点， 采用远点控制输出大转角，从而保证驾驶舒适性的需求，但由于预瞄机制的特性，如果单一采用远点预瞄难以保证车辆的跟随性保持在要求得范围内，引入近点控制则可以解决这个问题。
     由近点提供的补偿小转角可以将路径跟随性大大提高。因此采用远近两点预瞄，并根据不同工况来改变两点对转向输入的权值，这也正常人类驾驶习惯相符合。

3.2 经典预瞄模型的不足

    在传统的横向预瞄跟踪模型中大部分采用预瞄点横向偏差作为参考量，往往忽略了预瞄点的航向偏差带来的影响。经典预瞄模型的不足：

• 最优方向盘转角计算基于小转角假设。最优曲率模型建立在 “阿克曼几何关系”的基础上，最优曲率模型描述的关系仅仅在前轮转角非常小时才成立，也就是说大曲率将导致所估计的方向盘转角会有很大偏差。
• 模型中缺少方向信息对最优转角估计的贡献。而人类驾驶员在驾驶过程当中，则是根据距离偏差和角度偏差共同控制方向盘转角。如图所示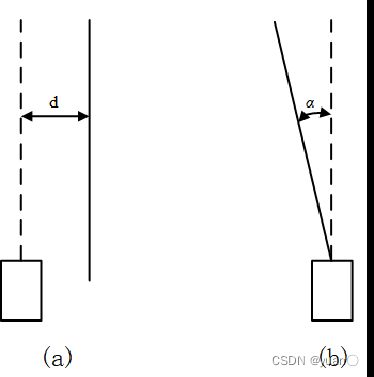：    (a)和(b)显示了两种不同转向工况，在(a)中横向偏差为d，航向偏差为0，驾驶员方向盘趋向于右转；
      在(b)中，虽然与道路的横向偏差为0，但航向偏差为$\alpha$，驾驶员方向盘趋向于左转。
      由此可见距离偏差与角度偏差都是驾驶员需要的重要的输入量，有经验的驾驶员通过这两个信息进行综合考虑，最终准确的估计出方向盘所需要的转动角度，如此循环，从而动态调整方向盘完成驾驶过程。

    虽然现在大部分学者所做研究只考虑距离偏差，其也能满足一些工况下的需求，某些情况下，角度偏差对驾驶员来说更重要，如图所示：    虚线代表车辆实际前进方向，实线代表期望路径，如果单单采用预瞄横向距离误差，如采用预瞄点1和预瞄点2，也就是采用了两个预瞄距离不同的预瞄点，得到的结果却截然相反：预瞄点1会使方向盘向左打，而预瞄点2却会使方向盘向右打。显然在这种情况下方向盘应向左打，这恰恰与角度偏差得出来的结果相吻合，所以这种情况下角度偏差具有更高的信任度。

3.3 横向预瞄控制

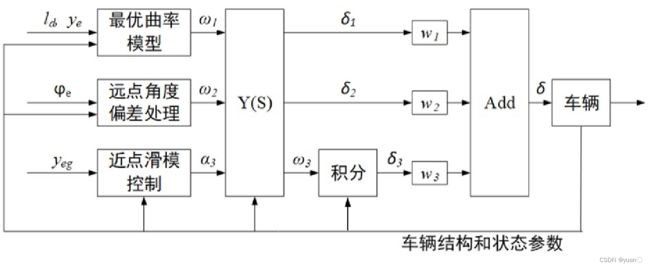
    横向预瞄建模过程如下图所示，主要包括：道路输入，控制量，校正环节，车辆，输出，控制决策等几个环节。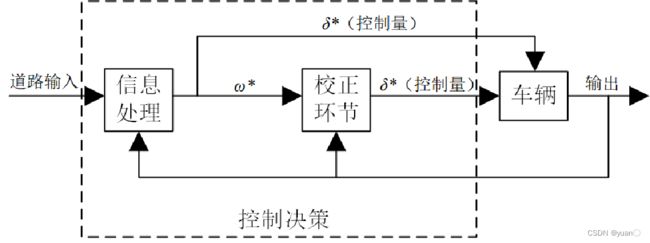
    本算法中，驾驶员转向控制所需获得的视觉信息包括了远、近两个预瞄点。每个点都能带来两个信息，即横向距离偏差与航向角度偏差。下图为远近预瞄点与道路与车辆参数之间的几何关系，其中共有四种视觉信息用来作为道路输入：$y_{e1}，y_{e2}，{\psi }_{e1}，{\psi }_{e2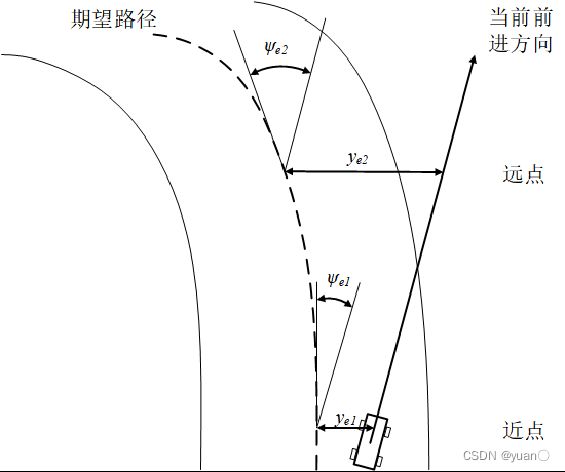}$。    将汽车前轴中心选作近处参考点，远处参考点由预瞄时间和汽车速度共同决定。该算法的目标为：
（1） 在经过预瞄时间$T_p$后，车辆位置与远点重合。
（2） 在经过预瞄时间$T_p$后，车辆航向与远点道路航向重合。
（3） 车辆行驶在道路中心线上，即$ye1\to 0$。
（4） 车辆行驶稳定，即${\psi }_{e1}\to 0$。

---

    由于远点和近点的控制目标是不相同的。对于远近两点提供的道路信息也采用不同的处理方式。
    对于远点则采用“最优曲率模型”，即假设车辆通过一个等半径圆弧路径在预瞄时间结束后到达预瞄点，存在一个最优的轨迹曲率$1/R^{\ast }$，并据此推断出理想车辆横摆角速度${\omega }^{\ast }$，之后通过校正环节得到${\delta }^{\ast }$。
    对于近点则采用滑膜控制得到控制量。对四个控制量进行加权计算，权值$w_1，w_2，w_3，w_4$得到最终结果。

3.3.1 横摆角速度与方向盘转角的传递函数

    通过建立车辆二自由度模型，可得到汽车动力学微分方程，并由此得出横摆角速度与方向盘转角的传递函数.
具体推导过程可以参考参考文献[1]、 [2] 、[3]
    得到的传递函数的大致形式为$$Y(s)=\frac{\delta }{\omega }(s)=\frac{i}{G_{\omega }}\cdot \frac{T_1\cdot S+1}{{\tau }_1\cdot S+1}$$

3.3.2 远点处误差信息处理

    远点处误差信息处理主要通过距离误差和角度误差的输入来实现。    对于远点横向误差输入需要获得最优转向半径 R。
首先不考虑车辆质心侧偏角计算最优转向半径（图中虚线）。
    由几何关系可得：
$$R^2=l_d^2+(R-y_e{)}^2$$    化简得：
$$R=(l_d^2+y_e^2)/(2\cdot y_e)$$    下面将质心侧偏角$\beta$引入考虑，经过观察，其实质上是将原坐标系$xoy$旋转了$\beta$度得到新坐标系$x’oy$’。即求预瞄点在坐标系$x’oy$’中的坐标$l_d’$和$y_e’$。
    根据旋转坐标系转换方程：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}\cos \beta & \sin \beta \\ -\sin \beta & \cos \beta \end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$    可得：$$l_d^{\prime }=cos\beta \cdot l_d+sin\beta \cdot y_e$$$$y_e^{\prime }=-sin\beta \cdot l_d+cos\beta \cdot y_e$$    同理根据几何关系得到理想转向半径$R$：$$\mathrm{R}=\frac{{{\mathrm{l}}^{\prime }}_{\mathrm{d}}^2{+{\mathrm{y}}^{\prime }}_{\mathrm{e}}^2}{2\times {{\mathrm{y}}^{\prime }}_{\mathrm{e}}}$$    由稳态圆周转向运动公式得：$${\mathrm{w}}_1=\frac{\mathrm{v}}{\mathrm{R}}=\frac{v2\times {{\mathrm{y}}^{\prime }}_{\mathrm{e}}}{{{\mathrm{l}}^{\prime }}_{\mathrm{d}}^2{+{\mathrm{y}}^{\prime }}_{\mathrm{e}}^2}$$    理想方向盘转角：$${\delta }_1={\omega }_1\cdot Y(s)$$    对于航向角度偏差的道路信息输入如上图，获取理想横摆角速度可以直接由公式得：${\omega }_2={\phi }_e/T_p$
    式中 $T_p$为预瞄时间，由此可得远点角度误差修正方向盘转角：${\delta }_2={\omega }_2\cdot Y(S)$

3.3.3 近点处误差信息处理

    $y_{ef}$为前轴中心处横向距离误差，$y_{eg}$为质心处横向距离误差，${\phi }_{en}$为近点处航向角偏差。
    在此假设道路为直线，且前轮转角很小，车辆近似看做直线运动。
    在近点误差信息处理中，角度偏差可用距离偏差的一阶导表示，并统一加到滑膜面中共同研究。通过一系列的计算分析，得到近点控制所得到的的方向盘转角为：${\delta }_3={\int }_0^t{\alpha }_3\cdot Y(S)dt$(此式只是一个表示形式，具体表达式暂不列出)
    一般通过判断${\delta }_3$的变化率（$\frac{{\delta }_3(t+\Delta t)-{\delta }_3(t)}{\Delta t}$）的大小来判断其对系统稳定性的影响程度。
    但是，由于近点控制不利于方向盘的稳定性，因此希望近点控制在方向盘变化比较剧烈时不起作用。
    设置一个判别条件来限制角度输出量的大小：$$\left|\frac{{\delta }_3(t)-{\delta }_3(t-T)}{T}\right|>K_{SW}$$
    $\delta (t)$为$t$时刻的方向盘转角，$K_{sw}$为角速度阈值，取值为30rad/s，如果上式满足，输出${\delta }_3(t)$=${\delta }_3(t-T)$；否则${\delta }_3={\int }_0^t{\alpha }_3\cdot Y(S)dt$.
    最终的方向盘转角为
$$\delta =w_1\cdot {\delta }_1+w_2\cdot {\delta }_2+w_3\cdot {\delta }_3$$
其中， $w_1,w_2,w_3为{\delta }_1,{\delta }_2,{\delta }_3$的权值，且$w_1=1,w_2=0.15,w_3=1$.

3.3.4 横向部分控制框图

3.4 纵向预瞄控制

3.4.1 获取目标速度

    纵向控制的控制目标是在预瞄时间后达到预瞄速度，预瞄速度主要由远点处的道路曲率决定(但在实际解决问题中，还需要考虑其他因素。例如，在跟车时，预瞄速度需要与前车的行驶速度保持一致)。

3.4.2 获取目标加速度

    假设汽车在预瞄时间Tp 内由车速v 匀加速至预瞄速度vd，所需预瞄加速度为：$a_d=(v_d-v)/T_p$

3.4.3 获取目标踏板开度

    根据$a_d$的大小确定开度。$a_d$>0时，执行加速踏板，并根据$MAP$图获取踏板开度；$a_d$<0时，根据相关判断，可不执行任何操作，依靠行驶阻力减速，也可执行制动踏板，开度由制动器结构决定。

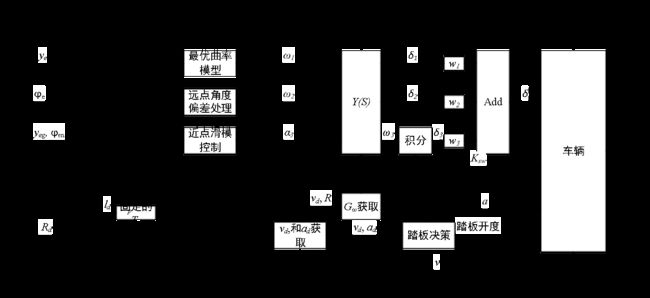
3.4.4 纵向部分控制框图

3.5 综合控制（汽车横纵向运动的耦合）

    汽车正常行驶过程中，纵向车速和方向盘转角存在一定的耦合关系，其中主要是纵向车速对横向运动特性的影响，本模型主要考虑了两点：车速对预瞄距离ld的影响和对横摆角速度增益Gω的影响。

3.5.1 对预瞄距离$l_d$的影响

    远点的位置由车速和预瞄时间决定.

3.5.2 对横摆角速度增益$G_{\omega }$的影响

    经仿真验证，Gω不仅会受纵向车速v影响，也会受转弯半径r影响，如图所示。

3.5.3 综合控制模型控制框图

3.6 仿真分析相关结果

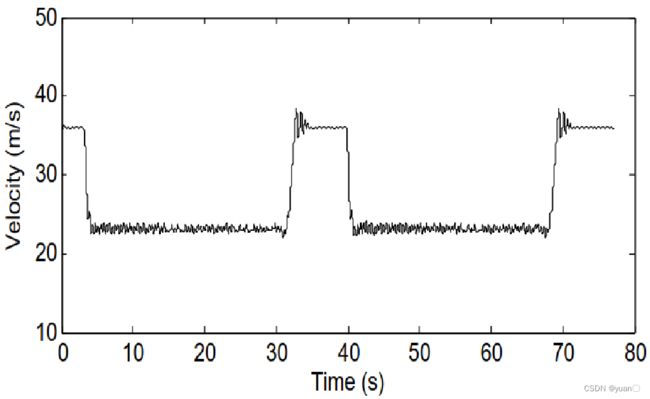
3.6.1 纵向车速

    纵向车速可以随着道路曲率的变化而变化。

3.6.2 横向误差

    可见，采用近点控制可以使车辆进入弯道时产生的误差逐渐收敛至0，且，近点控制权值越大，收敛速度越快。

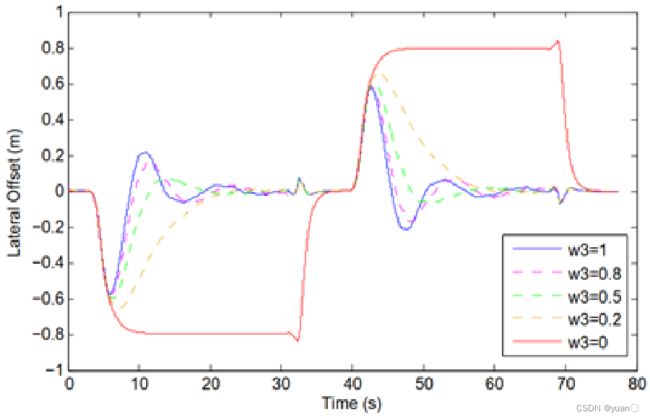
3.6.3 跟踪结果

    与横向误差对应，采用近点控制后的模型使汽车入弯后向目标路径靠拢，其靠拢速度也随着近点控制的权值增大而增大。

3.6.4 方向盘转角

    采用近点控制可以在汽车转弯时消除横向偏差，提高跟踪精度，但是方向盘的调整也会因此更加频繁，幅度也会变大

---

声明

本人所有文章仅作为自己的学习记录，若有侵权，联系立删。

参考文献

[1] 张廓然. 考虑驾驶员特性的网联车辆轨迹规划算法研究[D].东南大学,2020.DOI:10.27014/d.cnki.gdnau.2020.002940.
[2] 线性二自由度汽车模型对前轮角阶跃输入的稳态响应分析（matlab/simulink）
[3] 车辆工程（1）——线性二自由度汽车模型的运动方程