神经网络笔记一：Non-stationary Transformers: Exploring the Stationarity in Time Series Forecasting

摘要

现在Transformer在时间序列预测上发挥巨大作用，但对于非平稳的现实时间序列表现并不好。之前的一些研究着重在于将时间序列平稳化，这样的方法减弱了对突发事件的预测，同时在时间序列预测方面的效果下降。本文称之为过度平稳化（over-stationarization）,即Transformer对于不同的时间序列产生了相似的Attention，减弱了模型预测能力。针对这种现象，本文进而提出了Non-stationary Transformers框架，其中包含两个模块：
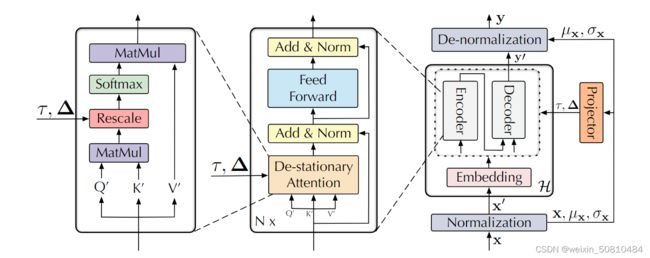
分别是序列平稳化模块（Series Stationarization）以及逆平稳化模块（De-stationary Attention）。序列平稳化模块之中，本文将模块输入的数据的统计量与模块输出结合。逆平稳化模块则设计为从不同时间序列中习得不同Attention，利用这些Attention恢复时间序列固有的非平稳性。

时间序列的非平稳性：时间序列的统计特征和联合分布随着时间变化而变化，非平稳性使得时间序列更加不可预测。
上图为三段不平稳时间序列的Attention的可视化图。我们可以看到在本文的模型中，不平稳时间序列的Attention能够产生明显的差异，说明不平稳时间序列本身的固有属性能够帮助我们进行预测。而Over stationarization问题就是将时间序列平稳化，而没有利用到非平稳序列的固有属性。

本文贡献

• 发现了非平稳时间序列的预测能力，以及现有平稳化方法造成的过平稳化问题。
• 提出了Non-stationary Transformers 避免过平稳化的现象。
• Non-stationary Transformers 在六个基准上，超过了四个现今主流的Transformer模型。

Non-stationary Transformers

1 Series Stationarization

1.1 Normalization module

class MyDataset(Dataset):
	...
	def __getitem__(self,index):
		s_begin = index
		#其中S就是seq_len
		s_end = s_begin + self.seq_len
		# seq_x[0,0]的长度为C
		seq_x = self.data_x[s_begin:s_end]
		seq_y = self.data_y[s_begin:s_end]
		return(seq_x,seq_y)

通过移动窗口的方式得$S$长度的序列，每个序列具有$C$长度的特征。
$${\mu }_x=\frac{1}{S}\sum _{i=1}^S{x}_i,{\sigma }_x^2=\frac{1}{S}\sum _{i=1}^S(x_i-{\mu }_x{)}^2,x_i^{{}^{\prime }}=\frac{1}{{\sigma }_x}\odot (x_i-{\mu }_x)$$
其中 $x=[x_1,x_2,...,x_S{]}^T\in {\mathbb{R}}^{S\times C},x^{{}^{\prime }}=[x_1^{{}^{\prime }},x_2^{{}^{\prime }},...,x_S^{{}^{\prime }}{]}^T\in {\mathbb{R}}^{S\times C}$,$S$ 和 $C$ 分别是序列的长度和变量个数。

1.2 De-normalization module

在经过整个模型$H$后，可以得到O长度的向量$y^{{}^{\prime }}=[y_1^{{}^{\prime }},y_2^{{}^{\prime }},...,y_O^{{}^{\prime }}]$，将其利用先前计算的${\sigma }_x,{\mu }_x$进行标准化逆变换，我们可以得到$\hat{y}=[{\hat{y}}_1,{\hat{y}}_2,...,{\hat{y}}_O]$.这个过程可以总结为以下公式：$$y^{{}^{\prime }}=H(x^{{}^{\prime }}),{\hat{y}}_i={\sigma }_x\odot (y_i^{{}^{\prime }}+{\mu }_x)$$

1.3 De-stationary Attention

我们仅仅通过1.2中的逆标准化，并没法还原时间序列的非平稳性，所以要通过模型内部更加复杂的机制实现这件事情。为了实现这个事情，我们利用De-stationary Attention 机制去获得原始非平稳数据的时间相依关系。

1.3.1对一般模型的分析

从Self-Attention 开始：$$Attn(Q,K,V)=Softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$
其中$Q,K,V\in {\mathbb{R}}^{S\times d_k}$ 。输入数据为$x=[x_1,x_2,...,x_S{]}^T$,并且$Q=[q_1,q_2,...,q_S{]}^T=[f(x_1),f(x_2),...,f(x_S){]}^T$。通过标准化后，$x^{{}^{\prime }}=[x_1^{{}^{\prime }},x_2^{{}^{\prime }},...,x_S^{{}^{\prime }}{]}^T=(x-1{\mu }_x^T)/{\sigma }_x,Q^{{}^{\prime }}=[q_1^{{}^{\prime }},q_2^{{}^{\prime }},...,q_S^{{}^{\prime }}{]}^T=[f(x_1^{{}^{\prime }}),f(x_2^{{}^{\prime }}),...,f(x_S^{{}^{\prime }}){]}^T$。假设$f$是线性函数，$Q^{{}^{\prime }}=(Q-1{\mu }_Q^T)/{\sigma }_x$。同样的我们对于$K^{{}^{\prime }},V^{{}^{\prime }}$有类似的结果。可以得到以下结果：
$$\begin{gathered} Q^{{}^{\prime }}{K}^{{}^{\prime }T}=(Q-1{\mu }_Q^T)/{\sigma }_x[(K-1{\mu }_K^T)/{\sigma }_x{]}^T \\ =\frac{1}{{\sigma }_x^2}(Q{K}^T-1({\mu }_Q^T{K}^T)-(Q{\mu }_K)1^T+1({\mu }_Q^T{\mu }_K)1^T) \end{gathered}$$

$$Softmax(Q{K}^T)=Softmax(\frac{{\sigma }_x^2{Q}^{{}^{\prime }}{K}^{{}^{\prime }T}+1({\mu }_Q^T{K}^T)+(Q{\mu }_K)1^T-1({\mu }_Q^T{\mu }_K)1^T}{\sqrt{d_k}})$$
因为${\mu }_Q^T{\mu }_K$是常数,$(Q{\mu }_K)1^T$每一列都相同故可化简为以下形式

$$Softmax(Q{K}^T)=Softmax(\frac{{\sigma }_x^2{Q}^{{}^{\prime }}{K}^{{}^{\prime }T}+1({\mu }_Q^T{K}^T)}{\sqrt{d_k}})$$

$Softmax(Q{K}^T)$从非平稳序列$x$可以直接算出，从式子可以看出原序列的信息不仅仅包含平稳化后的信息$Q^{{}^{\prime }},K^{{}^{\prime }}$，而且包括${\sigma }_x,{\mu }_Q,K$等非平稳序列的信息。

1.3.2 De-stationary Attention

为了恢复初始的Attention，即$Softmax(Q{K}^T)$，我们需要得到${\sigma }_X^2,\Delta =K{\mu }_Q\in {\mathbb{R}}^{S\times 1}$。我们将这些所需量，定义为逆平稳因子（de-stationary factors）。值得注意的是，我们先前对$f$的线性假设，通常是不成立的，因此我们要从$x,Q,K$学习到相应的逆平稳因子。我们对De-stationary Attention的定义如下：
$$\begin{gathered} log\tau =MLP({\sigma }_x,x),\Delta =MLP({\mu }_x,x), \\ Attn(Q^{{}^{\prime }},K^{{}^{\prime }},V^{{}^{\prime }},\tau ,\Delta )=Softmax(\frac{\tau Q^{{}^{\prime }}{K}^{{}^{\prime }T}+1{\Delta }^T}{\sqrt{d_k}})V^{{}^{\prime }} \end{gathered}$$

代码实现

Nonstationary_Transformers