2022.10.23 第五次周报

---

前言

本周完成了两项工作，一是文献的阅读，二是再次对cnn深入了学习。

一、文献阅读

本周阅读了这篇文章《FILTER-AND-CONVOLVE: A CNN BASED MULTICHANNEL COMPLEX CONCATENATION ACOUSTIC MODEL》。
这篇文章提出了一种基于卷积神经网络(CNN)的多通道复域级联声学模型。该模型从多通道噪声语音信号中提取特定语音信息。此外，针对多声道复杂串接声学模型，设计了两个适用性较广的CNN模板和几种说话人自适应方法。

问题背景

在多通道语音识别中，需要同时记录多个信号。来自多个记录的空间信息通常被波束形成器以空间滤波器的形式使用。然而，空间滤波可能无法充分利用多个信号中包含的特定语音信息。在此之前都是使用波束形成器Beamformers衰减来自其他方向的噪声，但随后有人提出多通道级联声学建模工作试图充分利用多通道中特定于语音的信息，但代价是无法从显式的空间信息中获益，以及用感知线性预测(PLP)特征串联起来等方法都不能优化。

思想来源

基于DNN的时频掩蔽被证明对于准确估计转向向量和功率谱密度(PSD)矩阵非常有效，这可以看作是将语音相关信息合并到波束形成器中的一种方法。在这项工作中，作者提出了一个多通道级联声学模型，该模型在对噪声信号进行空间滤波后提取特定语音信息。与传统的单耳系统相比，观察到持续的改善。使用BeamformIt和MVDR波束形成器作为前端。

系统描述

在作者的滤波卷积系统中，他们用声学模型中的可训练卷积层来代替波束形成器中的求和运算。

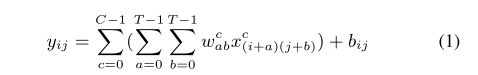
整个系统的示意图：

先是将多通道信号送入波束形成器进行空间滤波。然后对滤波后的信号进行预处理，分别转换到频域。在拼接后，频域特征被用作我们基于CNN的多通道复杂拼接声学模型的输入，该模型包括一个卷积层、常规特征提取模块和一个内部单耳声学模型。

区别于其他的联合波束形成器-声学模型系统

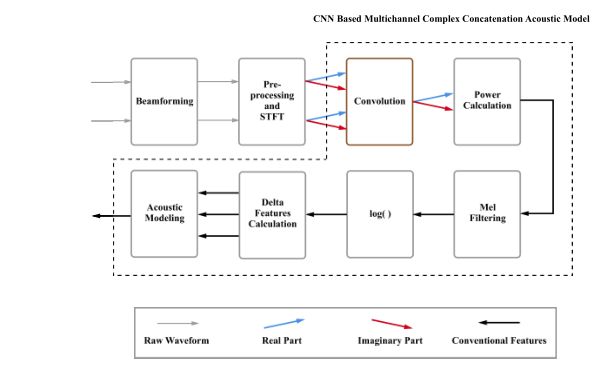
大多数联合波束形成器-声学模型系统直接对空间滤波后的信号进行求和，而作者的系统使用可训练的卷积层来提取特定于语音的信息。作者设计了两种卷积层模板，加权CNN模板和复杂CNN模板。加权CNN方法共享每个通道的实部和虚部模板，而复杂CNN模板的设计使每个通道的卷积操作模仿复杂乘法。

两种模板的示意如下图。输出的实部记为or，虚部记为oi，通道c的实部记为rc，虚部记为ic。对于加权CNN方法，通道c的模板记为tc。对于复杂的CNN方法，通道c使用了两个模板，分别为tcr和tci。

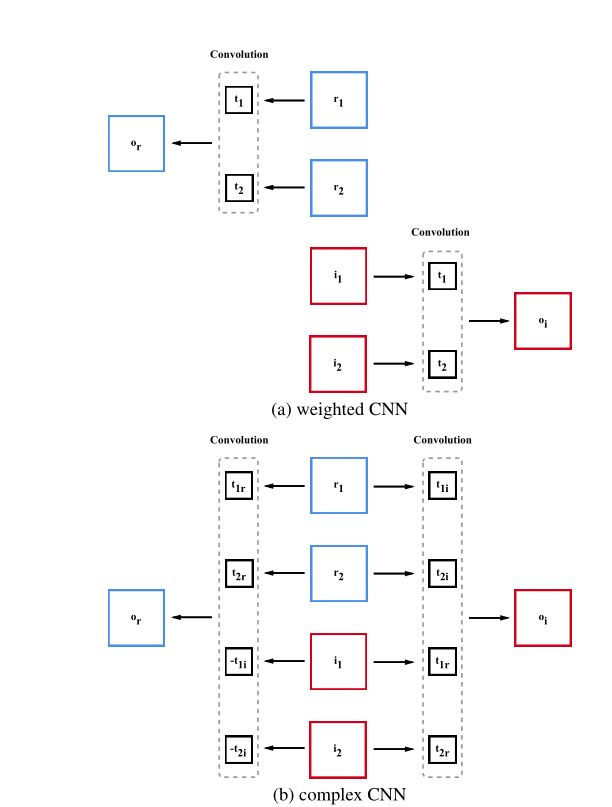
作者的模型使用了四种无监督说话人自适应方法，三种方法基于线性输入网络(LIN)，第四种方法基于线性隐藏网络(LHN)。并且设计了三种基于LIN的模板共享方法:共享模板、针对不同通道的不同模板、针对不同通道和不同复杂组件的不同模板。基于LHN的方法在内部单耳声学模型的输入处增加了一个线性层，模拟了传统单耳声学模型的LIN自适应。

文献总结

提出了一种基于CNN的多通道复杂级联声学模型。它不仅利用了多信号中的空间信息，还利用了语音信息。除了适用于各种波束形成器前端的后端外，该模型还可以被视为迈向多通道声学模型的一步，该模型使用对不同话语的自适应网络隐式嵌入波束形成器。

二、卷积神经网络

在计算机视觉领域中，手写数字分类问题就相当学习计算机语言的“hello world”。经过上两周的学习，在刚开始处理手写数字分类问题时，首先想到的当然是全连接神经网络。
MNIST数据库中相同大小（28×28）的数字图片：

上面这些大小为28×28的图片，用全连接神经网络确很好解决。因为28×28=784，只需要把每一个图片当成是784维的矢量，然后输入784维的输入层中，再堆叠几层隐藏层，最后以10个节点的输出层结束，每一个节点对应一个数字就可以了。

1.全连接神经网络遇到的问题

1.1.信息量问题

但这只是一个28×28的小型图片，而我们日常在计算机视觉领域上处理的图片已经达到了224x224或更大。构建一个神经网络来处理224x224彩色图像：包括图像中的3个颜色通道（RGB），结果是224 x 224 x 3 = 150528个输入特征！在这样的网络中，典型的隐藏层可能有1024个节点，因此我们必须为第一层训练150，528 x 1024 = 1.5亿多个权重。我们的网络将是巨大的，几乎不可能训练。

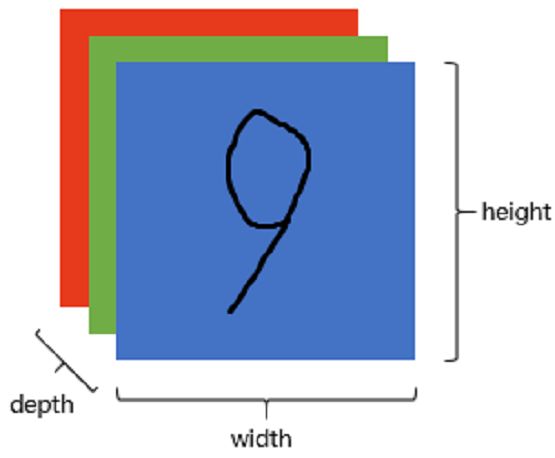
1.2.空间位置变性

在识别一张图片是猫或者是狗时，如果原图和被识别的图片上的动物的背景，位置，大小都一样时，这就很容易识别，用全连接神经网络，从全局的角度，对像素进行逐一核对，不难判断。但这是不现实的，因为动物是会动的，拍照的角度是会动的，所以很难重全局的角度去识别是猫还是狗。
下面这张图清晰的从位置、角度、大小、光泽等特征分析了用全连接方式识别图片时存在的问题。

2.卷积神经网络是什么

为了解决上面存在的两个问题，所以引入了卷积神经网络的概念。
卷积神经网络是为了处理数据量过大，而改变从全局特征的角度开始向局部特征角度转变的神经元连接方式。卷积神经网络最主要的是卷积核，也叫过滤器，其作用就是从局部的角度分析相邻像素点之间的关系。用同一个的卷积核对同一张图片进行一个单元格一个单元格（卷积核的大小）的方式向前扫描就可以知道，只考虑一个角度的情况下图片被分析成什么样子。
下面从垂直和水平两个角度处理图片像素之间的关系。

了解卷积核的基本概念之后，开始正式介绍CNN。
CNN的全称是Convolutional Neural Network，是一种前馈神经网络。由一个或多个卷积层、池化层以及顶部的全连接层组成。
卷积层(Convolutional Layer) - 主要作用是提取特征。
池化层(Max Pooling Layer) - 主要作用是下采样(downsampling)，却不会损坏识别结果。
全连接层(Fully Connected Layer) - 主要作用是分类。

2.1.卷积层

卷积层，是基于卷积的数学运算而构建出来处理神经元关系的结构。
卷积在数学含义中是两个变量在某范围内相乘后求和的结果。
其中星号*表示卷积。当时序时，序列是的时序i取反的结果；时序取反使得以纵轴为中心翻转180度，所以这种相乘后求和的计算法称为卷积和，简称卷积。另外，是使位移的量，不同的对应不同的卷积结果。
在卷积层也做了类似的操作，但如今的学习的时候用互相关(cross-correlation)代替卷积（convolution）。从技术上讲，我们（以及许多CNN实现）实际上在这里使用互相关而不是卷积，但它们几乎做同样的事情。我不会在这篇文章中讨论其中的区别，因为它并不那么重要，但如果你好奇，请随时查找卷积（convolution）与互相关(cross-correlation)的一点探讨。
卷积层由一组滤波器组成，您可以将其视为数字的2维矩阵。
下面是一个示例 3x3 筛选器（卷积核）：

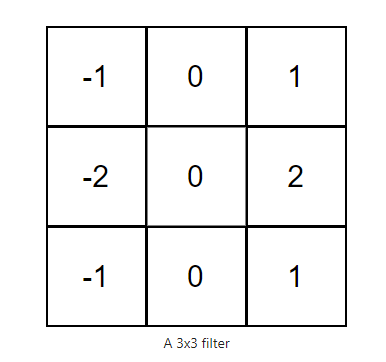
在卷积操作中，通常是输入图像和滤波器，通过将滤波器与输入图像卷积来生成输出图像。这包括4步：

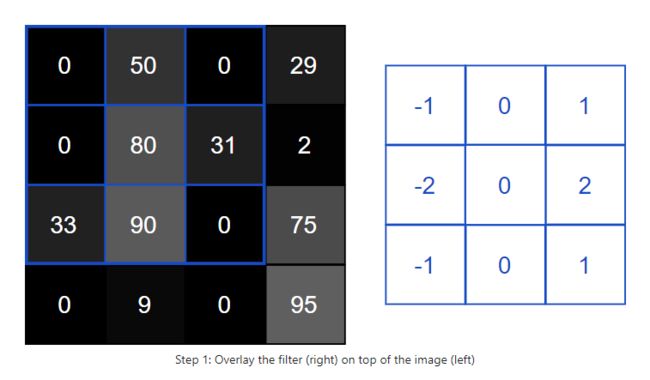
1.将滤镜叠加在图像顶部的某个位置。
2.在滤镜中的值与图像中的相应值之间执行元素乘法。
3.总结所有元素方面的产品。此总和是输出图像中目标像素的输出值。
4.对所有位置重复此操作。

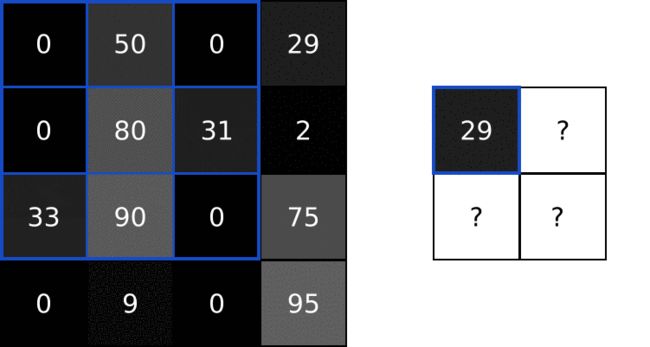
将输入图像的局部信息和卷积核相乘然后相加，会得到一下成像：
0x（-1）+50x0+0x1+0x（-1）+80x0+31x2+33x（-1）+90x0+0x1=62-33=29

我再进一步公式化，把卷积核看成是一个权重的矩阵（以2x2为例）：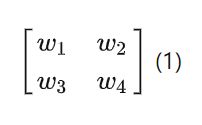
那么卷积核和对应的元素相乘再相加的结果，也会和前馈神经网络一样，加上一个偏移量，最后得出如下结果：

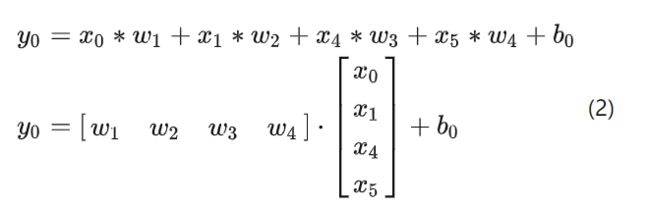
以4x4的图片为例，在2x2卷积核扫描完整张图片之后，会得出以下结果：

2.1.1维度

上面展示的图片是2维灰度图的，但实际上图片RGB模式的，所以图片往往是3维的（也称通道）。
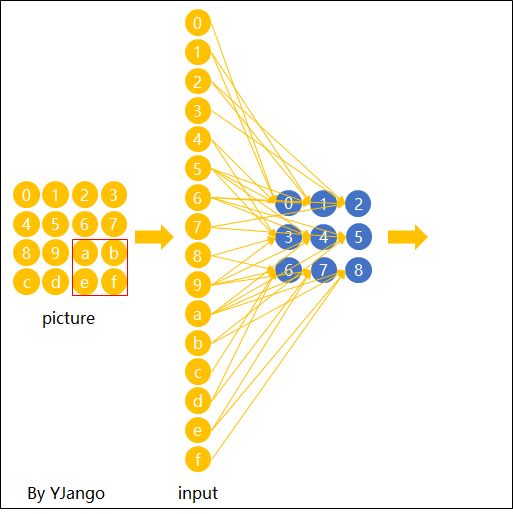
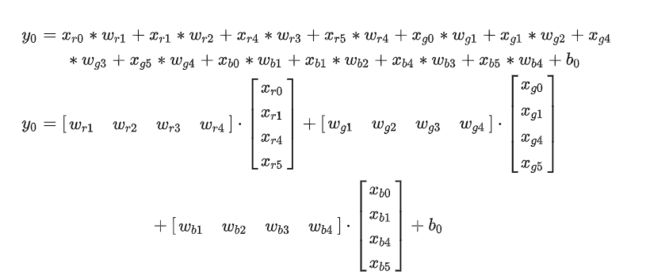
下面这张图展示了，在维度为复数时，卷积核是如何连接输入节点到输出节点的。 图中红、绿、蓝颜色的节点表示3个维度。 黄色节点表示一个卷积后得到的输出节点。 其中被透明黑框圈中的12个节点会被连接到黄黑色的节点上。

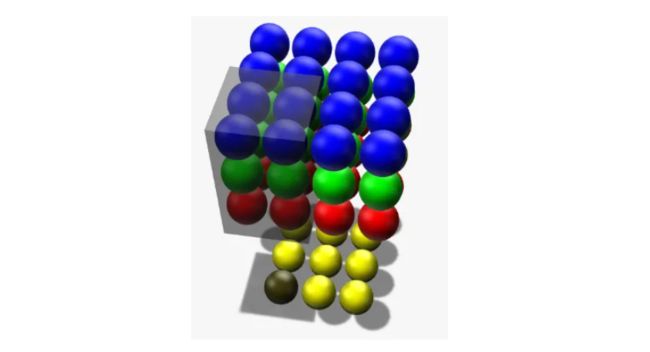
因为3个维度之间是不共享权重的，所以会出现三组权重：

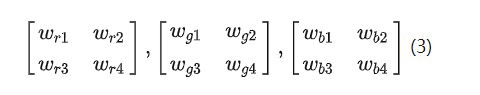
在卷积核的的处理后，3个维度的特征值分别相乘再相加求和，得出的结果介绍上图的黄黑色小球，公式如下：

2.1.2零填充

观察上图看可以发现，原本是4x4的图片，再经过卷积之后输出的结果变成3x3的特征矩阵了。通常，我们更希望输出图像的大小与输入图像的大小相同。为此，我们在图像周围添加零，以便输出的结果和原图像有一样的大小。所以4x4 原图需要 1 像素的填充：

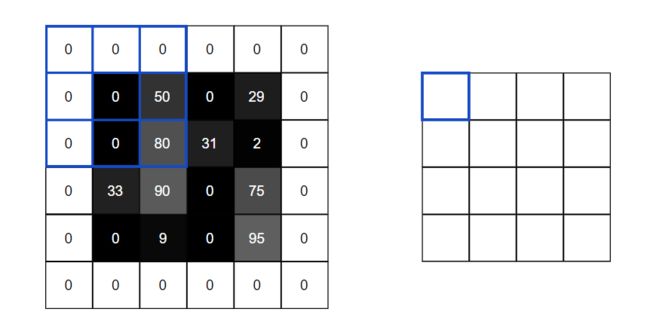
经过零填充之后，卷积得到结果就和原图是一样大小了。

2.2.池化层

图像中的相邻像素往往具有相似的值，在卷积核处理之后的图片也是如此，因此为了解决信息都是冗余的问题，引入了池化操作pooling。池化层所做的就是把卷积层处理后的特征矩阵再处理，取其中更有代表性的特征值，忽略部分不影响整体的特征值。池化操作有max、min或average，这里只提max 池化。
max pooling的操作如下图所示：整个图片被不重叠的分割成若干个同样大小的小块（pooling size）。每个小块内只取最大的数字，再舍弃其他节点，最后得到原有的平面结构但小了一圈的特征矩阵：

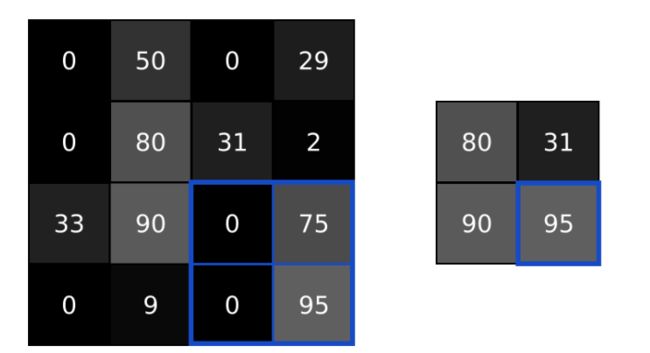
2.3.全连接层（也叫前馈层）

当抓取到足以用来识别图片的特征后，接下来的就是如何进行分类。 全连接层（也叫前馈层）就可以用来将最后的输出映射到线性可分的空间。 通常卷积网络的最后会将末端得到的长方体平摊(flatten)成一个长长的向量，并送入全连接层配合输出层进行分类。
为了完成我们的CNN，我们需要赋予它实际做出预测的能力。为此，我们使用了Softmax函数来解决多类分类问题。
再次用到前面提到的MNIST数据库中28×28的数字图片，经过卷积层，用8个卷积核处理输出变成了26x26x8的长方形矩阵；再经过池化层2x2的max pooling处理，输出变成了13x13x8的长方形矩阵。最后的全连接层，则是把13x13x8的矩阵先用flatten()函数平摊成长长的8个一维向量，再将使用具有 10 个节点的 softmax 层（一个节点代表每个数字）作为 CNN 中的最后一层。层中的每个节点都将连接到每个输入。应用软最大变换后，概率最高的节点所表示的数字将是 CNN 的输出！

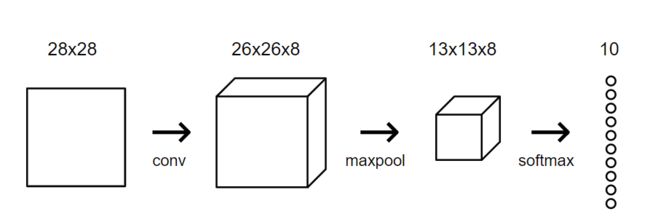
再解释一下softmax函数。Softmax函数，是逻辑函数的一种推广。它能将一个含任意实数的K维向量z“压缩”到另一个K维实向量σ(z)中，使得每一个元素的范围都在(0,1)之间，并且所有元素的和为1。该函数多用于多分类问题中。

2.3.1交叉熵

既然最后的输出以概率为评判标准，那么肯定存在误差，所以在sotfmax函数作用输出的概率下，引入了交叉熵作为评估的方法，对每个预测结果进行准确程度的评价。
Loss： L=−ln(pc)
当pc等于1的时候，表示完全准确，所以损失程度为0，当只有80%的时候，损失程度就是0.223。
如：pc=1,L=−ln(1)=0；pc =0.8,L=−ln(0.8)=0.223。
这里的L表示损失程度，所以越小越好。

3.如何实现卷积神经网络

在经过上面的一层一层的推导之后，我们不调用keras库用，将上面的思路，用代码实现上面的每一步操作。
图片来源是MNIST，图片大小为28×28，用8个卷积核。

3.1卷积层实现

class Conv3x3:
  # A Convolution layer using 3x3 filters.

  def __init__(self, num_filters):                # num_filters：过滤器的数量
    self.num_filters = num_filters
    self.filters = np.random.randn(num_filters, 3, 3) / 9                 # 初始化随机过滤器三维数组filters
    # print (self.filters)

  def iterate_regions(self, image):

    h, w = image.shape

    for i in range(h - 2):
      for j in range(w - 2):
        im_region = image[i:(i + 3), j:(j + 3)]             # im_region：一个包含相关图像区域的3x3阵列
        yield im_region, i, j                               #  yield 的用法：https://www.icode9.com/content-1-1386849.html

  def forward(self, input):
    h, w = input.shape
    output = np.zeros((h - 2, w - 2, self.num_filters))

    for im_region, i, j in self.iterate_regions(input):
      output[i, j] = np.sum(im_region * self.filters, axis=(1, 2))     
                        #axis=(1, 2)：(0,1,2)代表三维数组的高度x宽度x长度，长度为第三维度指num_filters过滤器的数量，因为我们只希望在后面两个维度（宽度x长度）
                        #axis是一个整型的元组类型，则在多个轴上执行求和，而不是在单个轴上执行求和了。
                        # np.sum()，产生一个长度为1d的数组，其中每个元素包含相应过滤器的卷积结果。
                        # output[i,j] 表示输出中像素的卷积结果（i，j）
    return output

3.2池化层实现

class MaxPool2:
  def iterate_regions(self, image):

    h, w, _ = image.shape                            # 将原来的图像大小缩小一半
    new_h = h // 2
    new_w = w // 2

    for i in range(new_h):
      for j in range(new_w):
        im_region = image[(i * 2):(i * 2 + 2), (j * 2):(j * 2 + 2)]        #2*2的过滤器，为了不重复，每次移动两步。
        yield im_region, i, j

  def forward(self, input):

    h, w, num_filters = input.shape
    output = np.zeros((h // 2, w // 2, num_filters))            #生产 num_filters 个新的矩阵

    for im_region, i, j in self.iterate_regions(input):
      output[i, j] = np.amax(im_region, axis=(0, 1))               # 挑2*2矩阵中最大的值MAX

    return output

3.3全连接层实现

class Softmax:
  def __init__(self, input_len, nodes):
    # We divide by input_len to reduce the variance of our initial values           
    self.weights = np.random.randn(input_len, nodes) / input_len                     #input_len表示长*宽*高的个数
    self.biases = np.zeros(nodes)

  def forward(self, input):

    self.last_input_shape = input.shape

    input = input.flatten()                                                        #flatten()，把维度是a*b*c的矩阵，换成维度只有一维的，有a*b*c个元素的矩阵

    self.last_input = input

    input_len, nodes = self.weights.shape

    totals = np.dot(input, self.weights) + self.biases
    self.last_totals = totals

    totals = np.dot(input, self.weights) + self.biases                              # softmax函数 求概率
    exp = np.exp(totals)
    return exp / np.sum(exp, axis=0)

再用交叉熵评估预测的准确性：

def forward(image, label):
  # We transform the image from [0, 255] to [-0.5, 0.5] to make it easier
  # to work with. This is standard practice.
  out = conv.forward((image / 255) - 0.5)
  out = pool.forward(out)
  out = softmax.forward(out)

  # Calculate cross-entropy loss and accuracy. np.log() is the natural log.
  loss = -np.log(out[label])
  acc = 1 if np.argmax(out) == label else 0

  return out, loss, acc

整体的代码是实现为：

import mnist
import numpy as np
from conv import Conv3x3
from maxpool import MaxPool2
from softmax import Softmax

# We only use the first 1k testing examples (out of 10k total)
# in the interest of time. Feel free to change this if you want.
test_images = mnist.test_images()[:1000]
test_labels = mnist.test_labels()[:1000]

conv = Conv3x3(8)                  # 28x28x1 -> 26x26x8
pool = MaxPool2()                  # 26x26x8 -> 13x13x8
softmax = Softmax(13 * 13 * 8, 10) # 13x13x8 -> 10

def forward(image, label):
  '''
  Completes a forward pass of the CNN and calculates the accuracy and
  cross-entropy loss.
  - image is a 2d numpy array
  - label is a digit
  '''
  # We transform the image from [0, 255] to [-0.5, 0.5] to make it easier
  # to work with. This is standard practice.
  out = conv.forward((image / 255) - 0.5)
  out = pool.forward(out)
  out = softmax.forward(out)

  # Calculate cross-entropy loss and accuracy. np.log() is the natural log.
  loss = -np.log(out[label])
  acc = 1 if np.argmax(out) == label else 0

  return out, loss, acc

print('MNIST CNN initialized!')

loss = 0
num_correct = 0
for i, (im, label) in enumerate(zip(test_images, test_labels)):
  # Do a forward pass.
  _, l, acc = forward(im, label)
  loss += l
  num_correct += acc

  # Print stats every 100 steps.
  if i % 100 == 99:
    print(
      '[Step %d] Past 100 steps: Average Loss %.3f | Accuracy: %d%%' %
      (i + 1, loss / 100, num_correct)
    )
    loss = 0
    num_correct = 0

MNIST CNN initialized!
[Step 100] Past 100 steps: Average Loss 2.302 | Accuracy: 11%
[Step 200] Past 100 steps: Average Loss 2.302 | Accuracy: 8%
[Step 300] Past 100 steps: Average Loss 2.302 | Accuracy: 3%
[Step 400] Past 100 steps: Average Loss 2.302 | Accuracy: 12%

这是输出的结果，很明显这神经网络损失太大，而且准确率也很低，这是因为权重都是random（）随机生成的，没有训练，所以接下来对神经网络进行梯度下降的权重训练。

4.卷积神经网络的倒推

训练神经网络通常包括两个阶段：

1.正向阶段，其中输入完全通过网络。
2.一个向后阶段，其中梯度被反向传播（反向传播）并更新权重。

因为这个卷积神经网络的输出是10个数字，所以需要一个10位的数组装载输出，并且有卷积层，池化层，和全连接层三层，所以进行三次梯度下降操作。

gradient = np.zeros(10)
# ...

# Backprop
gradient = softmax.backprop(gradient)
gradient = pool.backprop(gradient)
gradient = conv.backprop(gradient)

所以这是我们的第一步。
第二步是做好相对应的缓存，因为向后倒推是需要用到前面的值的，所以在向前推的时候需要保存部分数值，以备向后倒退时使用。
如这些值：

self.last_input_shape = input.shape
self.last_input = input
self.last_totals = totals

接着开始编写各个层的梯度下降公式。

4.1.倒推全连接层

最后输出的结果是由多个函数组合而成，所以一一逐步分解函数，然后求偏导。

紧接着开始求偏导：

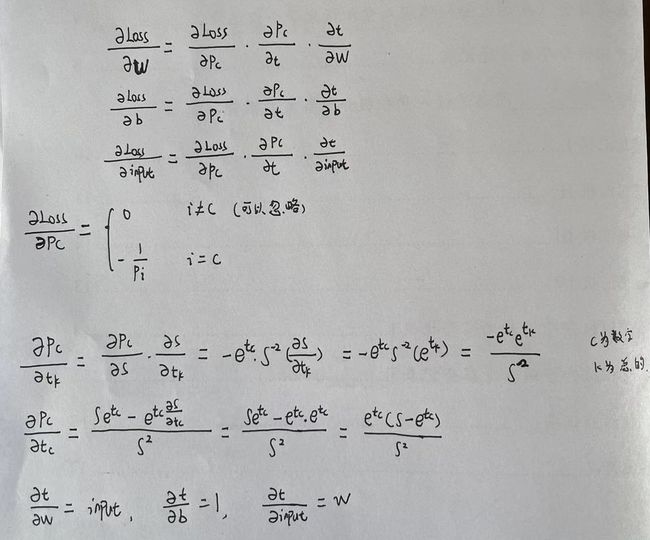
计算完所有梯度后，剩下的就是实际训练Softmax层！我们先使用随机梯度下降 （SGD） 更新权重和偏差，就像我们在全连接神经网络中所做的那样，然后返回d_L_d_inputs，同时要注意，我们添加了一个learn_rate参数，用于控制我们更新权重的速度。此外，我们必须在返回d_L_d_inputs之前reshape(）重塑，因为我们在正向传递期间flattened（）扁平化输入。

def backprop(self, d_L_d_out, learn_rate):
    '''
    Performs a backward pass of the softmax layer.
    Returns the loss gradient for this layer's inputs.
    - d_L_d_out is the loss gradient for this layer's outputs.
    - learn_rate is a float    '''
    # We know only 1 element of d_L_d_out will be nonzero
    for i, gradient in enumerate(d_L_d_out):
      if gradient == 0:
        continue

      # e^totals
      t_exp = np.exp(self.last_totals)

      # Sum of all e^totals
      S = np.sum(t_exp)

      # Gradients of out[i] against totals
      d_out_d_t = -t_exp[i] * t_exp / (S ** 2)
      d_out_d_t[i] = t_exp[i] * (S - t_exp[i]) / (S ** 2)

      # Gradients of totals against weights/biases/input
      d_t_d_w = self.last_input
      d_t_d_b = 1
      d_t_d_inputs = self.weights

      # Gradients of loss against totals
      d_L_d_t = gradient * d_out_d_t

      # Gradients of loss against weights/biases/input
      d_L_d_w = d_t_d_w[np.newaxis].T @ d_L_d_t[np.newaxis]
      d_L_d_b = d_L_d_t * d_t_d_b
      d_L_d_inputs = d_t_d_inputs @ d_L_d_t

      # Update weights / biases
      self.weights -= learn_rate * d_L_d_w
      self.biases -= learn_rate * d_L_d_b
      return d_L_d_inputs.reshape(self.last_input_shape)

4.2.倒推池化层

最大池化层无法训练，因为它实际上没有任何权重，但我们仍然需要实现一个 backprop（） 方法来计算梯度。我们将再次从添加正向阶段缓存开始。这次我们需要缓存的只是输入，也就是最大值的位置：

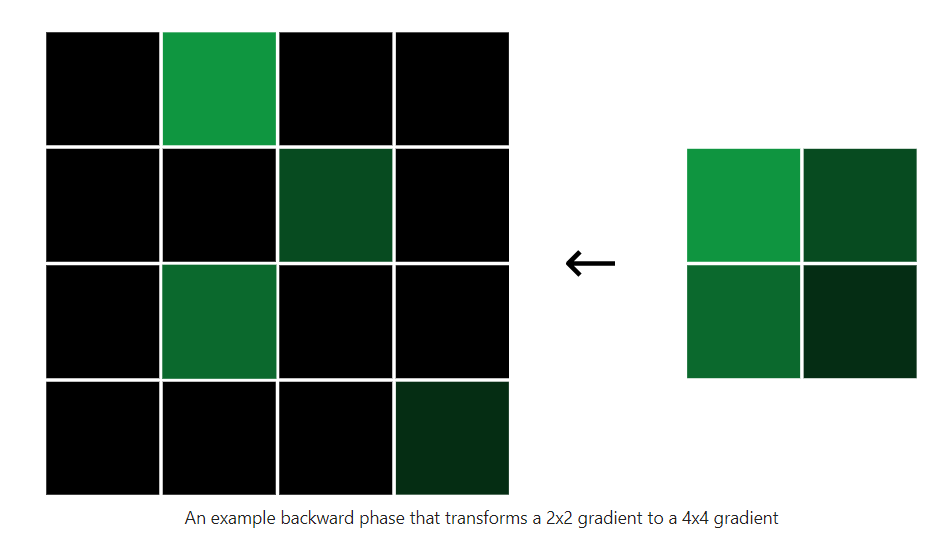
注意箭头的方向，是倒退回去的。
下面是代码的实现：

    h, w, _ = image.shape
    new_h = h // 2
    new_w = w // 2

    for i in range(new_h):
      for j in range(new_w):
        im_region = image[(i * 2):(i * 2 + 2), (j * 2):(j * 2 + 2)]
        yield im_region, i, j

还原最大值的位置，其他位置补零，虽然输入像素不是原来的值，但它们对整体影响为不大，所以稍微更改该值根本不会改变输出！

  def backprop(self, d_L_d_out):
    d_L_d_input = np.zeros(self.last_input.shape)       #还原一个全为零的数组

    for im_region, i, j in self.iterate_regions(self.last_input):
      h, w, f = im_region.shape
      amax = np.amax(im_region, axis=(0, 1))             #挑选出最大值

      for i2 in range(h):
        for j2 in range(w):
          for f2 in range(f):
            # If this pixel was the max value, copy the gradient to it.    #还原最大值
            if im_region[i2, j2, f2] == amax[f2]:
              d_L_d_input[i * 2 + i2, j * 2 + j2, f2] = d_L_d_out[i, j, f2]

    return d_L_d_input

4.3.倒推卷积层

有了全连接神经网络的倒推基础，卷积层的倒推其实并不复杂，区别就是要先记录好原先的位置，再对应找位置的权重进行梯度下降。
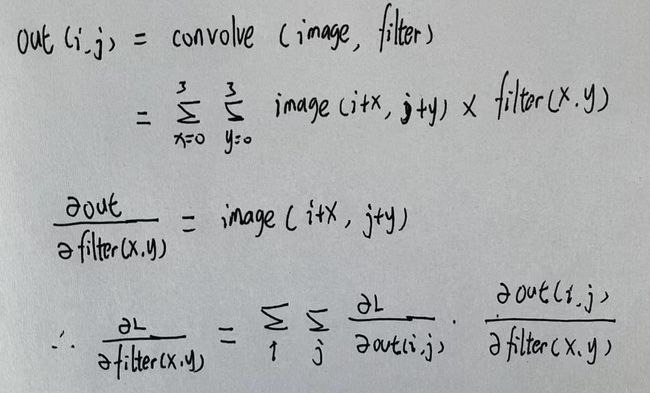代码实现：

def backprop(self, d_L_d_out, learn_rate):

    d_L_d_filters = np.zeros(self.filters.shape)

    for im_region, i, j in self.iterate_regions(self.last_input):
      for f in range(self.num_filters):
        d_L_d_filters[f] += d_L_d_out[i, j, f] * im_region

    # Update filters
    self.filters -= learn_rate * d_L_d_filters

    # 我们在这里没有返回任何东西，因为我们使用Conv3x3作为CNN 中的第一层.
    return None

这就是全部卷积神经网络的介绍，由于代码过长，所以不在此展示，需要可以联系我。

总结

本周对cnn的了解不仅停留在正向推导，而是对反向传播也进行了学习，并且了解了每一层的意义和传播中每个值的含义。