利用PyG实现端到端的链路预测+社区检测（组合优化）

链路预测和社区检测

在之前的博客《利用PyG实现社区检测经典算法ClusterNet》中已经对社区检测、论文、ClusterNet已经做了非常详细的介绍，并且讲解了如何使用Pytorch Geometric工具包在cora数据集实现纯优化的社区检测。本文主要是对以链路预测和社区检测作为代表的学习+优化组合的任务进行实现。 这里简单再对概念进行介绍和拓展。

网络中的链路预测(Link Prediction)是指如何通过已知的网络节点以及网络结构等信息预测网络中尚未产生连边的两个节点之间产生链接的可能性。简单来说，我们的任务可以等价为 给定一个删除一定比例边的网络后，去预测其中缺失的边。
社区检测(community detection)又被称为是社区发现，它是用来揭示网络聚集行为的一种技术。社区检测实际就是一种网络聚类的方法，通俗来讲就是将具有相同特性和不同特性的节点进行结构划分。网络社区划分的优劣往往通过模块度来进行衡量。一个网络不通情况下的社区划分对应不同的模块度。模块度越大，对应的社区划分也就越合理;如果模块度越小，则对应的网络社区划分也就越模糊。本项目采用模块度作为优化的目标，其计算函数会在下面进行一定的解释。
在实际问题中，两个问题往往是结合在一起的。比如，我们往往会对输入先进行链路预测，然后再对预测完复原的图进行社区检测的任务。这种分两阶段的方法模型一方面会大大提高实现的复杂性，同时无法保证链路预测对社区检测的目标（分别代表学习和优化两个任务）是否起到有效帮助。而论文《End to end learning and optimization on graphs》提出了一种端到端的方法，将两个任务有效地结合到了一起，并且取得了非常不错的效果。
在下文实现的代码中，** 我们的目的是，通过只知道的40%的边来预测出完整的图（链路预测）并进行优化任务（社区检测）。 **

论文介绍——端到端的学习与优化

这篇文章《End to end learning and optimization on graphs》2019年发表在人工智能和机器学习领域的国际顶级会议 NeurIPS上。在之前的传统方法中，往往是先对对图的学习问题进行解决，再进行优化。在实际应用中，图的学习和优化问题常常是结合在一起，比如图或相关属性往往只是部分观察到，引入了一些学习问题，如链接预测，必须在优化之前解决。文章作者提出了一种端到端的方法，将学习问题和优化问题结合到了一起，将优化问题作为学习任务的一层，运用下游的优化误差反过来传递到学习的任务上，这允许模型特别关注下游任务，它的预测将用于该任务。
实验结果表明，作者的ClusterNet系统优于纯端到端方法（直接预测最优解决方案）和完全分离学习和优化的标准方法。
作者源码见GitHub：https://github.com/bwilder0/clusternet

技术方法ClusterNet

作者以链路预测和社区检测分别作为学习任务和优化任务。
引用我师兄的解释，具体上，文章假定在进行社区检测之前，网络结构不是完全已知的，只有部分（假设40%）网络结构是能够观察到的，所以要先用链路预测来找出出网络中那些没有被观察到的连边，然后再在这种“复原”后的网络上进行社区检测，利用模块度指标来评估社区检测的效果。 同时，文章还设立了对照实验，即在原始网络（不隐藏任何连边）上执行社区检测任务，通过观察两组实验的结果来分析他们提出的模型的有效性。
在文中，作者提出了一种端到端的模型ClusterNet，先让数据经过两层GCN进行嵌入，再将卷积网络的输出放入K means聚类函数中进行迭代聚类，最后运用输出的分配矩阵和模块度进行损失计算（即优化目标），反向传递并进行参数优化。
**在本人看来，核心在于在其中将优化任务作为学习任务中的一层进行误差的反向传播。**通俗地讲，就是用优化问题的目标作为损失函数来更新学习问题的卷积参数。这允许模型特别关注下游的实际任务，它的预测将更好地作用于该任务。 在本文中，作者以链路预测和社区检测分别作为学习任务和优化任务。
模型结构如下图所示：
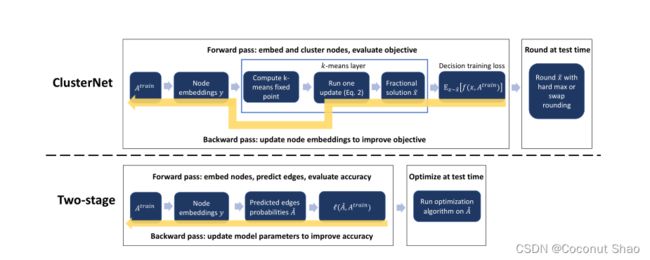上图：ClusterNet，下图：典型的学习+优化两阶段方法。 可以看出，传统的方法分为两部分，互相之间没有交叉。
特别注意的是，在K means聚类中我们可以得到软分配矩阵， 在训练过程中我们在softmax过程中会进行软分配，即用概率来描述节点分配到不同簇的概率，这样对参数的优化会更为准确；而在测试过程中，我们会加大softmax的硬度（hard）系数，甚至每一百轮使用100作为硬度系数（代码中也叫cluster_temp）来对r进行乘积再进行softmax操作，使其变为非0即1的硬划分。 这样对分配结果有更好的展示，也可以计算实际的预测损失。
在ClusterNet中，作者使用模块度作为优化的目标，具体公式如下：

其中r为软分配矩阵，d为节点的度，A为邻接矩阵。具体的计算过程会在下面代码讲解的地方讲到。

作者在多个不同数据集上进行了测试。为了方便对比，作者设计了一种没有聚类的端到端方法GCN-e2e，这种方法可以视为将所有的节点视为一个社区，这样便没有外部节点，也算是一种最优。对比可以看出，聚类的存在可以将精度大幅提升：

这也进一步证明了聚类层在社区检测任务中的不可或缺。
下面将使用PyG对Cora数据集进行以链路预测和社区检测作为学习和优化问题的代表的复现。

基于PyG下的Cora数据集实现组合优化

我们选择在Cora数据集上进行论文优化部分的代码复现。Cora数据集是图优化问题的一个经典的单图数据集，来源于论文Revisiting Semi-Supervised Learning with Graph Embeddings，包含2708篇科学出版物， 10556条边，每个节点有其独自的类别，总共7种类别。数据集中的每个出版物都由一个 0/1 值的词向量描述，表示字典中相应词的缺失/存在。 该词典由 1433 个独特的词组成。意思就是说每一个出版物都由1433个特征构成，每个特征仅由0/1表示。PyG中Cora数据集的具体的参数如下图：

在实现数据集引入和处理方面，本人主要使用了PyTorch Geometric这个库，这是我的大牛师兄推荐的一个比较简单的处理图问题的函数库，它的函数兼容性好并且操作相比于networkx较为简单（个人感觉哈），内置了大量数据集的自下载及其处理方式。具体介绍可以见官网：https://pytorch-geometric.readthedocs.io/en/latest/

写在实现代码前面，本项目的目的是，通过只知道的40%的边来预测出完整的图（链路预测）并进行优化任务（社区检测）。

总体思路概述

前面博客中，我们虽然将优化任务作为学习任务中的一层进行误差的反向传播，但实际情况中，网络结构不是完全已知的，只有部分（假设40%）网络结构是能够观察到的，所以要先用链路预测来找出出网络中那些没有被观察到的连边，然后再在这种“复原”后的网络上进行社区检测，利用模块度指标来评估社区检测的效果。

我们仍然使用PyG来对论文进行复现，在模型搭建上，我们选择上述的方法一，我们同样通过PyG的内置函数来对边进行划分。在对边进行40%提取时采用了PyG的内置函数：train_test_split_edges，有效减少了40%边构建邻接矩阵的复杂度。
与上面纯优化不同的是，我们输入模型进行训练的是数量为实际边数40%的链接，从而得到的软分配矩阵为用40%链接训练得出的r。在训练过程中也是采用这40%的边构建的归一化邻接矩阵adj_train来计算模块度train_object，并对模块度train_object，训练得出的软分配矩阵r和adj_train来进行损失计算和误差的反向传播——这就是链路预测（学习任务）之后用模块度目标（优化目标）来对链路预测的参数进行更新。
同时，我们在测试时，会将用train_object训练出来的分配矩阵r进行硬化（即用非常大的硬度系数使其变为硬分配矩阵，如前面概念所讲），与到test_object（所有边计算出的的模块度）计算损失，来验证分配结的社区结果在全图上的结果和精度。

导入需要的包

import torch
import torch.nn.functional as F
from torch_geometric.datasets import Planetoid
from torch_geometric.nn import GCNConv
from torch_geometric.utils import train_test_split_edges
import numpy as np
import scipy.sparse as sp
from models import cluster, GCNClusterNet

这里我们直接使用PyG内自带的GCN卷积核，这个类的输入为PyG格式的edge_index，而不需要提前转换成adj的邻接矩阵格式，可以说是数据集拿过来不用处理就可以做卷积，在学习问题和优化问题上都非常的便捷。

导入Cora数据集

这里利用PyG的格式直接导入Cora数据集：

dataset = Planetoid(root='../tmp/Cora', name='Cora')
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
data = dataset[0].to(device)

运行完之后可以看到，在data中的参数分别为：edge_index=[2, 10556], test_mask=[2708],
train_mask=[2708], val_mask=[2708], x=[2708, 1433], y=[2708]。具体的代表意义上述PyG官网有详细的例子，讲解的非常清晰。可以看到，这里对边的存储格式并不是以邻接矩阵adj的2708x2708的形式，而是直接用相连边的起点和终点构成的2x10556。

模型搭建GCNClusterNet

这个模型在纯优化内容的博客时有所讲解(PyG方法一)，但是由于引入了链路预测，部分代码存在差异。
首先我们定义一个GCN_NET，并用它对PyG格式的图进行一个双层的卷积。可以看到代码中，如果我们想要实现组合优化，那么pure_opt应当为False，我们只使用40%的边（data.train_pos_edge_index，后面会讲如何得到）和所有的节点feat作为图卷积的输入。这标识着我们假设只知道完整图40%的边。

class GCN_NET(torch.nn.Module):
    def __init__(self,nfeat,nhid, nout, dropout):
        super().__init__()
        self.conv1 = GCNConv(nfeat, nhid)
        self.conv2 = GCNConv(nhid,nout)
        self.dropout = dropout
    def forward(self, data,pure_opt):
        if pure_opt:
            x, edge_index = data.x, data.edge_index
        else:
            x , edge_index = data.x, data.train_pos_edge_index

        x = self.conv1(x, edge_index)
        x = F.relu(x)
        x = F.dropout(x,self.dropout , training=self.training)
        x = self.conv2(x, edge_index)
        return x

其次我们定义我们的主角——GCNClusterNet。我们讲上面定义的GCN_NET作为初始化的一个变量，对输入的图根据是否优化来进行卷积。可以看到，我设置了pure_opt默认为False，这标志着我们默认进行学习+优化的任务。
GCNClusterNet的初始化参数分别为：
nfeat——图的节点特征维度；
nhid=50——双层GCN隐藏层维度；
nout=50——双层GCN输出层维度；
dropout=0.2——双层GCNdropout参数；
K=5——聚类的cluster数量；
cluster_temp=50——softmax后的突出程度即硬度系数，官方解释为：how hard to make the softmax for the cluster assignments。
具体的输出层维度隐藏层维度等参数在模型训练代码的第一行指定。

我们先对图通过GCN_NET，即对40%的边和节点进行两层的GCN得到节点嵌入embeds，再将这个卷积网络的输出放入K means聚类函数中进行迭代聚类，输出分配矩阵（各个节点分配到各个社区结构的概率）等。返回参数具体为 ：
embeds——节点embedding，即未经历cluster进行K means的GCN输出，维度为节点数量xGCN的输出层，即2708x50；
mu——cluster means，维度为聚类系数Kx输出层，即5x50;
r——软分配矩阵，维度为节点数量x聚类系数K，即2708x5；
dist——节点相似性，即每个点到每个簇中心的距离，维度为节点数量x聚类系数K，即2708x5。

class GCNClusterNet(torch.nn.Module):
    def __init__(self, nfeat, nhid, nout, dropout, K, cluster_temp):#nfeat=1433, nhid=50, nout=50, dropout=0.2, K=5, cluster_temp=50
        super(GCNClusterNet, self).__init__()
        self.GCN_NET = GCN_NET(nfeat,nhid, nout, dropout)
        self.distmult = torch.nn.Parameter(torch.rand(nout))
        self.sigmoid = torch.nn.Sigmoid()
        self.K = K
        self.cluster_temp = cluster_temp
        self.init = torch.rand(self.K, nout)

    def forward(self, data, num_iter=1, pure_opt=False):
        embeds = self.GCN_NET(data,pure_opt)
        mu_init, _, _ = cluster(embeds, self.K, 1, num_iter, cluster_temp=self.cluster_temp, init=self.init)
        mu, r, dist = cluster(embeds, self.K, 1, 1, cluster_temp=self.cluster_temp, init=mu_init.detach().clone())
        return mu, r, embeds, dist

模块度矩阵函数和损失函数（优化目标）

我们要用优化（社区检测）的目标作为损失反过来对学习任务（链路预测）进行梯度传递，而在社区检测任务中，我们使用模块度作为社区检测好坏的标准。
在模块度矩阵函数中，先对邻接矩阵进行对角线清0，再求和生成度矩阵，最后将二者带入论文的公式中生产模块度矩阵（分类好坏的评价标准）。
在损失函数中，利用软分配矩阵r，归一化后的邻接矩阵bin_adj模块度矩阵mod带入论文中的公式求得模块度损失，即我们优化的目标。

def make_modularity_matrix(adj):
    adj = adj * (torch.ones(adj.shape[0], adj.shape[0]) - torch.eye(adj.shape[0]))
    degrees = adj.sum(axis=0).unsqueeze(1)
    # degrees = torch.unsqueeze(degrees,1)
    mod = adj - degrees @ degrees.t() / adj.sum()
    return mod


def loss_modularity(r, bin_adj, mod):
    bin_adj_nodiag = bin_adj * (torch.ones(bin_adj.shape[0], bin_adj.shape[0]) - torch.eye(bin_adj.shape[0]))
    return (1. / bin_adj_nodiag.sum()) * (r.t() @ mod @ r).trace()

数据处理和参数设置

首先，我们要利用PyG中的边生成邻接矩阵进行归一化，从而对邻接矩阵进行模块度计算。如果我们进行学习+优化，我们需要40%边的邻接矩阵adj_train、adj_train得出的模块度train_object以及训练得到的软分配矩阵r进行优化目标计算，从而指导参数的更新，在测试时使用全图完整的邻接矩阵adj_all的模块度test_object对效果进行测试。如果是纯优化，我们只需要全图完整的邻接矩阵的模块度test_object来进行训练和测试。
下面normalize和sparse_mx_to_torch_sparse_tensor是辅助将边矩阵[2,10556]转换为邻接矩阵[2708x2708]的函数，分别对输入进行归一化和格式转换。
我们利用模块度矩阵函数得到我们的训练对象和测试对象——模块度，命名为train_object（40%边）和test_object（100%边）。

def normalize(mx):
    rowsum = np.array(mx.sum(1))  # 矩阵行求和
    r_inv = np.power(rowsum, -1).flatten()  # 每行和的-1次方
    r_inv[np.isinf(r_inv)] = 0.  # 如果是inf，转换为0
    r_mat_inv = sp.diags(r_inv)  # 转换为对角阵
    mx = r_mat_inv.dot(mx)  # D-1*A,乘上特征，按行归一化
    return mx


def sparse_mx_to_torch_sparse_tensor(sparse_mx):
	#将adj转换为tensor格式
    sparse_mx = sparse_mx.tocoo().astype(np.float32)
    indices = torch.from_numpy(
        np.vstack((sparse_mx.row, sparse_mx.col)).astype(np.int64))
    values = torch.from_numpy(sparse_mx.data)
    shape = torch.Size(sparse_mx.shape)
    return torch.sparse.FloatTensor(indices, values, shape)

features = sp.csr_matrix(data.x, dtype=np.float32)  # 取特征
adj = sp.coo_matrix((np.ones(data.edge_index.shape[1]), (data.edge_index[0, :], data.edge_index[1, :])),
                    shape=(data.y.shape[0], data.y.shape[0]), dtype=np.float32)
adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)
features = normalize(features)  # 特征归一化
adj = normalize(adj + sp.eye(adj.shape[0]))  # A+I归一化
# 将numpy的数据转换成torch格式
features = torch.FloatTensor(np.array(features.todense()))
adj = sparse_mx_to_torch_sparse_tensor(adj)
adj = adj.coalesce()
bin_adj_all = (adj.to_dense() > 0).float()
test_object = make_modularity_matrix(bin_adj_all)

与之前纯优化不同的是，我们输入模型进行训练的是数量为实际边数40%的链接，从而得到的软分配矩阵为用40%链接训练得出的r。在训练过程中也是采用这40%的边构建的归一化邻接矩阵adj_train来计算模块度train_object，并对模块度train_object，训练得出的软分配矩阵r和adj_train来进行损失计算和误差的反向传播——这就是链路预测（学习任务）之后用模块度目标（优化目标）来对链路预测的参数进行更新。
在对边进行40%提取时采用了PyG的内置函数：train_test_split_edges，有效减少了40%边构建邻接矩阵的复杂度。
下面代码表明，如果pure_opt为False，则我们还需要40%边的邻接矩阵adj_train和相应的模块度train_object。
计算方法与上面一样，只不过输入由100%的边信息变为了40%的边信息。
优化器我们完全采用原文作者使用的优化器参数。

num_cluster_iter = 1
losses = []
val_ratio=0.3
test_ratio=0.3
pure_opt = False
K = 5
if not pure_opt:
    data = train_test_split_edges(data, val_ratio=val_ratio,test_ratio=test_ratio)
    model_cluster = GCNClusterNet(nfeat=data.x.size(1), nhid=50, nout=50, dropout=0.2, K=K, cluster_temp=50)

    adj_train = sp.coo_matrix((np.ones(data.train_pos_edge_index.shape[1]), (data.train_pos_edge_index[0, :], data.train_pos_edge_index[1, :])),
                        shape=(data.y.shape[0], data.y.shape[0]), dtype=np.float32)
    adj_train = adj_train + adj_train.T.multiply(adj_train.T > adj_train) - adj_train.multiply(adj_train.T > adj_train)
    adj_train = normalize(adj_train + sp.eye(adj_train.shape[0]))
    adj_train = sparse_mx_to_torch_sparse_tensor(adj_train)
    adj_train = adj_train.coalesce()
    bin_adj_train = (adj_train.to_dense() > 0).float()
    train_object = make_modularity_matrix(bin_adj_train)
else:
    model_cluster = GCNClusterNet(nfeat=data.x.size(1), nhid=50, nout=50, dropout=0.2, K=K, cluster_temp=50)
# model_cluster.train()
optimizer = torch.optim.Adam(model_cluster.parameters(), lr=0.01, weight_decay=5e-4)

模型训练

由于我们假设只已知40%的边，第一步我们对r（软分配矩阵），归一化后的adj_train（40%边得出的邻接矩阵），train_object（40%边得出的邻接矩阵计算得到的模块度）计算loss损失，取负数逆向求导，对参数进行优化。
当训练到500轮时，num_iter更改为5，增加cluster的迭代次数（K means更新的步骤数）。
每100轮迭代，我们将训练结果与test_object（所有边计算出的的模块度）计算损失，来验证分配结的社区结果在全图上的结果和精度，观察结果是否改善。其中我们对测试的softmax直接使用cluster_temp=100来突出其分配程度（相当于软分配转换为了硬分配，使其变为非1即0的矩阵，该节点在五个社区结构中概率最大的位置变为了1，其他概率都变为0）。
我们设置1001轮训练，保证训练结果的可靠性，同时使在最后一轮训练epoch=100的最后进行硬分配，然后测试训练结果（即优化目标的数值）。

for epoch in range(1001):
    mu, r, embeds, dist = model_cluster(data, num_cluster_iter, pure_opt=False)
    if not pure_opt:
        loss = loss_modularity(r, bin_adj_train, train_object)
    else:
        loss = loss_modularity(r, bin_adj_all, test_object)
    loss = -loss
    optimizer.zero_grad()
    loss.backward()
    if epoch == 500:
        num_cluster_iter = 5
    if epoch % 100 == 0:
        r = torch.softmax(100 * r, dim=1)
        if epoch ==1000:
            print(f"前10行训练得到分配矩阵{r[0:10,0:K]}")
    loss_test = loss_modularity(r, bin_adj_all, test_object)
    if epoch == 0:
        best_train_val = 100
    if loss.item() < best_train_val:
        best_train_val = loss.item()
        curr_test_loss = loss_test.item()
        # convert distances into a feasible (fractional x)#将距离转换为可行的（分数x）
        x_best = torch.softmax(dist * 100, 0).sum(dim=1)
        x_best = 2 * (torch.sigmoid(4 * x_best) - 0.5)
        if x_best.sum() > 5:
            x_best = 5 * x_best / x_best.sum()
    losses.append(loss.item())
    optimizer.step()

print(f'epoch{epoch + 1}   ClusterNet value:{curr_test_loss}')
if not pure_opt:
    print(f"链路预测+优化，已知{1.0-test_ratio-val_ratio}的边")

设置K=7时和K=5时的分配结果相似。当K=7时，输出结果如下图所示：

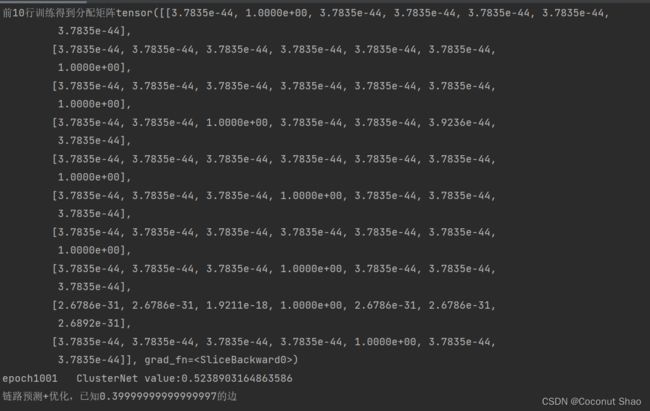
对比论文中的0.54，我们得到的0.52在合理误差范围内，可以认为结果一致。

补充

作者在原代码中使用的为40%的节点的特征和40%的边，而我们这里在GCN输入训练的为所有的节点的特征和40%的边，得到的结果差距不大。这也表明了链接和标签/特征的关系不大。推测该数据集标签与链接反映的信息不一样，有可能不同类别之间存在很多链接，而同类别中的链接占比不高。
为了测试该猜想，我们将完整的标签作为分配矩阵与所有边得出的模块度test_object进行优化计算（纯优化过程），得到社区分配的分数为0.64，甚至小于训练得出的分配数值。这有可能验证上述的猜想。


上图为训练得到的分数，下图为真实标签作为社区分配得到的分数。