解析Unity3D中计算法线矩阵的函数

如果法线简单地跟着顶点变换有时会出现如下图情况，
若图2所示，垂直关系变了.

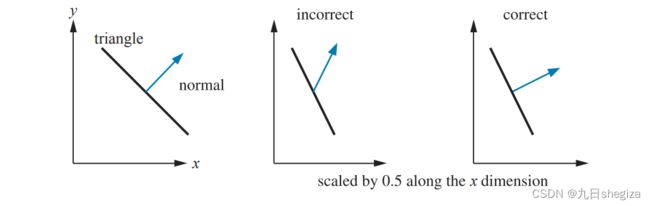
可以用线性代数知识证明
设原来的切线为$T$,法线$N$,则有
$$T^{T}N=0$$
如果切线经过缩放矩阵S变换,则新的切线为$T^{\prime }$,新的法线为$N^{\prime }$,
$$T^{\prime }=ST$$
假设$N^{\prime }$=SN,则有
$${\left(T^{\prime }\right)}^T{N}^{\prime }={\left(ST\right)}^T\left(SN\right)=T^T\left(S^{T}S\right)N$$
而缩放矩阵有以下特征
$$S=\left[\begin{array}{ccc}a& 0& 0\\ 0& b& 0\\ 0& 0& c\end{array}\right]$$

故有
$$S^{T}S=\left[\begin{array}{ccc}{a}^2& 0& 0\\ 0& b^2& 0\\ 0& 0& c^2\end{array}\right]$$

如果$a=b=c$,则$S=kE$,故
$${\left(T^{\prime }\right)}^T{N}^{\prime }=0$$
成立.否则则说明不能对法线应用和切线相同的变换.
类似地，如果对切线空间应用旋转矩阵$R$,则应该主要关注
$$R^{T}R?=kE$$
而我们知道旋转矩阵是正交矩阵，故上述关系肯定满足.
接下来是平移矩阵$Tr$,$Tr$的左$3\times 3$矩阵为$E$，故肯定也满足.

所以综合下来，只要缩放矩阵的Uniform的那么缩放，旋转，平移其一或多个组合组成$M$矩阵，则法线只需同左乘左$3\times 3M$就可以.如果不是uniform的，则需要不同的变换矩阵，而这个矩阵求法也跟上面的类似
$${\left(MT\right)}^T\left(?N\right)=0\to T^T{M}^T?N=0$$
只需$M^T?=E$即可故最终的$M^N$应为${\left(M^T\right)}^{-1}$,转置和求逆可以交换顺序,故结果同${\left(M^{-1}\right)}^T$,而$M^{-1}$即为世界坐标转为模型空间的矩阵$W$，即最终法线为$W^{T}N$而对一个矩阵转置比对一个向量转置更费时，故可以求最终法线的转置
$${\left(W^{T}N\right)}^T=N^{T}W$$
也即
$$N^{\prime }=\left\{N^{T}W.col0,N^{T}W.col1,N^{T}W.col2\right\}$$
Unity 3D中就是采用的这种思路
UnityObjectToWorldNormal函数可在UnityCG.cginc中找到

// Transforms normal from object to world space
inline float3 UnityObjectToWorldNormal( in float3 norm )
{
#ifdef UNITY_ASSUME_UNIFORM_SCALING
    return UnityObjectToWorldDir(norm);
#else
    // mul(IT_M, norm) => mul(norm, I_M) => {dot(norm, I_M.col0), dot(norm, I_M.col1), dot(norm, I_M.col2)}
    return normalize(mul(norm, (float3x3)unity_WorldToObject));
#endif
}

函数使用了一个宏 UNITY_ASSUME_UNIFORM_SCALING来判断是否需要特殊处理，不用特殊处理的话
则用以下函数

// Transforms direction from object to world space
inline float3 UnityObjectToWorldDir( in float3 dir )
{
    return normalize(mul((float3x3)unity_ObjectToWorld, dir));
}

如果需要则运用上面解释的方法计算正确的最终法线.