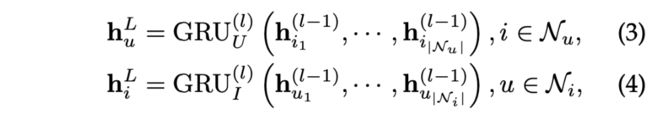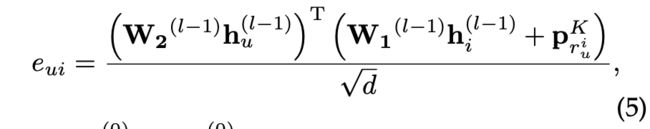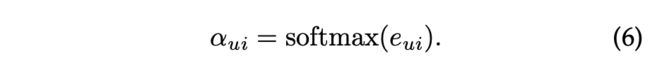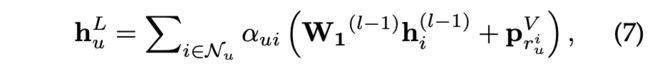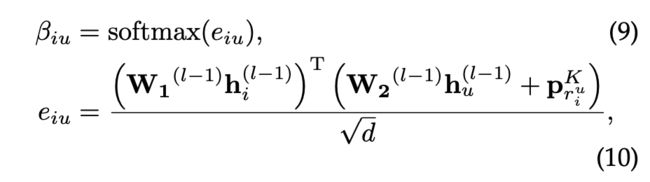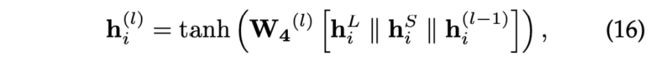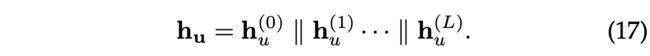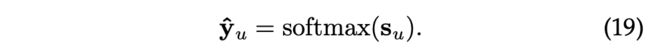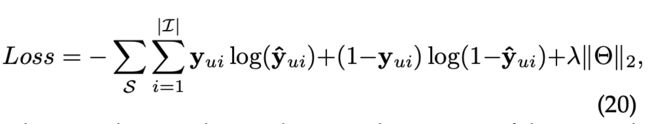【推荐系统-＞论文阅读】Dynamic Graph Neural Networks for Sequential Recommendation（用于序列推荐的动态图神经网络）

Dynamic Graph Neural Networks for Sequential Recommendation（用于序列推荐的动态图神经网络）

Mengqi Zhang, Shu Wu,Member, IEEE,Xueli Yu, Qiang Liu,Member, IEEE,Liang Wang,Fellow, IEEE

Abstract（摘要）

基于用户历史序列的用户偏好建模是序列推荐的核心问题之一。该领域的现有方法从传统方法到深度学习方法都有广泛的分布。然而，它们大多只在自己的序列内建模用户的兴趣，忽略了不同用户序列之间的动态协作信号，没有充分地探究用户的喜好。我们从动态图神经网络中获得灵感来应对这一挑战，将用户序列和动态协作信号建模到一个框架中。本文提出了一种新的方法——动态图神经网络序列推荐(DGSR)，该方法通过动态图结构将不同的用户序列连接起来，探索用户与具有时间和顺序信息的项目之间的交互行为。此外，我们设计了一个动态图推荐网络来从动态图中提取用户的偏好。从而将下项预测任务的序列推荐转化为动态图中用户节点与项目节点之间的链接预测。在三个公共基准上的大量实验表明，DGSR方法比几种最先进的方法表现更好。进一步的研究证明了通过动态图建模用户序列的合理性和有效性。

Index Terms-序列推荐，动态协作信号，动态图神经网络

1 Introduction（介绍）

随着互联网上信息量的急剧增长，推荐系统被用于帮助用户缓解电子商务、搜索引擎和社交媒体等在线服务中的信息超载问题。近年来，出现了几种协同过滤方法，它们主要关注统计用户与项目之间的交互[1]、[2]、[3]，而忽略了用户丰富的历史序列信息。然而，用户偏好会随着时间动态变化，随着历史交互项的变化而变化。因此，序列推荐是一种利用每个用户交互历史中的序列信息进行准确预测的推荐方法，受到了广泛的关注。

在序列推荐领域，提出了一系列的方法。例如，马尔可夫链模型[4]基于之前的交互进行推荐。一些基于RNN的模型[5]，[6]，[7]利用LSTM (long Short-term Memory)[8]或GRU (Gated Recurrent Unit)[9]网络来捕获用户序列中的顺序依赖关系。此外，卷积神经网络(CNN)和注意力网络在建模用户序列方面也很有效。例如，Caser[10]使用卷积过滤器来整合用户交互的顺序。SASRec[11]和STAMP[12]利用attention机制为项目之间的关系建模以捕获用户意图。近年来，图神经网络(GNNs)[13]、[14]受到越来越多的关注。受GNN在多种任务中成功应用的启发，提出了一些基于GNN的序列模型[15]、[16]、[17]，它们利用改进的GNN来研究每个序列中复杂项目转换关系。

虽然这些方法已经取得了令人信服的结果，但我们认为这些方法缺乏对不同用户序列之间的动态协作信号的显式建模，这主要表现在两个方面:

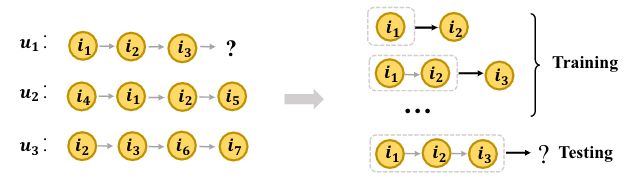
（1）这些模型没有显式地利用不同用户序列之间的协作信息，换句话说，它们大多侧重于对每个用户自身的序列进行编码，而忽略了不同用户序列之间的高阶连通性，如图1a所示，在图1a中，训练和测试过程中对用户序列的编码都在一个单一的序列中。但是，如图1b所示，在$t_3$时刻,$u_1$直接与$i_1$,$i_2$和$i_3$交互，并且与$u_2$和$u_3$以及它们的交互项有高阶连接。显然，$u_2$和$u_3$的交互信息可以帮助预测$u_1$的序列。这一信息被大多数现有的模型所忽略。

（2）这些模型忽略了高阶协作信息在不同时间的动态影响。从图1b中我们可以看到，由$u_1$的序列所形成的图及其高阶关联的用户和项目随着$t_1$,$t_2$和$t_3$时间的变化而变化。在这种情况下，$u_1$兴趣的变化不仅受到一阶交互项目$i_1$、$i_2$和$i_3$的变化的影响，还受到高阶连接用户和项目的变化的影响。同样，项目的语义信息也会随着一阶和高阶相关性的变化而变化。

(a) 左图表示$u_1$,$u_2$和$u_3$的不同序列。我们的目标是预测未来的互动。右边的图说明了大多数序列模型的训练和测试范例。

(b) $u_1$、$u_2$、$u_3$组成的用户-项目图在不同时间的交互。每条边代表了用户与项目之间的交互，并具有时间属性。节点$u_1$是要预测的目标用户。实线表示当前时间发生的交互。虚线箭头表示$u_1$的下一个交互。$u_1$的时间戳序列是(t1, t2, t3)

图1:用户物品顺序交互的图解。图(a)给出了$u_1$,$u_2$和$u_3$的交互序列。图(b)是$u_1$、$u_2$和$u_3$在不同时间的用户项交互图，可以看作是图(a)的精细化表示。

因此，以上两个方面导致了在序列推荐中难以准确捕获用户偏好。要应对这些挑战，需要解决两个重要问题：

（1）如何用图动态地表示用户项目交互。对于序列推荐来说，用户与项目之间的交互顺序至关重要。现有的大多数方法[3]将用户-项目交互表示为一个静态的二部图，但都不能记录用户-项目对的交互顺序。因此，我们需要考虑灵活有效地将序列信息或交互顺序整合到图中。

（2）如何对每个用户序列的动态协同信号进行显式编码。对于每个用户序列，其动态关联的项目和用户形成一个图结构，该图结构比传统的静态图包含更多的时间/顺序信息。从这个动态图中编码每个用户的偏好并不是一件简单的事情。

为此，受动态图表示学习[18]的启发，我们提出了一种新的动态图神经网络序列推荐方法(Dynamic Graph Neural Network for Sequential Recommendation, DGSR)，该方法通过动态图来探索用户和项目之间的交互行为。DGSR的框架如下:首先，我们将所有用户序列 转换为 边带时间和顺序信息的动态图(章节4.1)。因此，拥有公共项的用户序列通过“用户→项目” 和“项目→用户”连接相互关联。其次，我们设计了一种子图采样策略(章节4.2)来动态提取包含用户序列和关联序列的子图。第三，为了从子图中编码用户的偏好，我们设计了一个动态图推荐网络(DGRN)(章节4.3)，其中构建了一个动态注意模块来捕获用户的长期偏好和物品的长期特征，进一步利用循环神经模块或注意模块分别学习用户和物品的短期偏好和特征。通过多个DGRN层的叠加，可以更好地利用每个用户和每个项目节点丰富的动态高阶连通性信息。最后，我们的模型将下项预测任务转换为用户节点的链接预测任务(章节4.4)。在三个公共基准数据集上进行的大量实验验证了我们的DGSR方法的有效性。

综上所述，我们的工作做出了以下主要贡献:

• 我们强调了在序列推荐场景中明确建模用户序列之间的动态协作信号的关键重要性。
• 我们提出了一种新的基于动态图神经网络的序列推荐框架DGSR。
• 我们对三个真实世界的数据集进行了实证研究。大量实验证明了DGSR方法的有效性。

2 Related Work（相关工作）

2.1 Sequential Recommendation（序列推荐）

序列推荐是根据用户的历史交互序列预测下一个项目。与静态推荐系统相比，它通常根据用户的顺序交互生成用户表示进行预测。开创性的工作，如基于马尔可夫链的方法[4]，[19]基于k阶交互预测下一项。基于翻译的方法[20]模型与一个TransRec组件的三阶交互。

随着深度学习的发展，针对序列推荐任务提出了许多相关工作。GRU4Rec[5]是第一个将循环神经网络(RNN)用于基于会话的推荐任务的算法。由于RNN的优异性能，它被广泛应用于序列推荐任务[6]、[7]、[21]。此外，卷积神经网络(CNN)也被用于序列推荐，以研究不同的模式。基于CNN的Caser[10]模型采用卷积过滤器来整合用户交互的不同顺序。此外，注意力网络也是应用于序列推荐的有力工具。NARM[22]利用RNN的注意机制捕捉用户的主要目的。STAMP[12]使用一种新颖的注意力记忆网络，有效地捕捉用户的一般兴趣和当前兴趣。SASRec[11]将自注意机制应用于序列推荐问题，以显式地建模项目间的关系。最近，在SASRec的基础上，TiSASRec[23]被提出，来建模项目的绝对位置以及它们之间的时间间隔。

在过去的几年里，图神经网络(GNNs)在处理图结构数据方面取得了最先进的性能。也有一些研究[15]，[16]，[17]，[24]，[25]将GNN应用于序列推荐。SR-GNN[15]首先利用门控GNNss来捕获会话场景中复杂的项目转换关系。在此基础上，提出了一种结合个性化GNN和注意力机制的会话感知场景A-PGNN[16]。MA-GNN[25]采用增强记忆的图形神经网络，捕捉用户的长期和短期兴趣。

虽然这些基于GNN的模型在序列推荐方面显示出了很好的发展方向，但它们只关注于对序列内的用户偏好进行建模，而忽略了序列间的项目关系。为此，提出了一些模型。例如，HyperRec[26]采用超图对序列内或跨序列项之间的高阶相关连接进行建模。CSRM[27]通过计算与当前会话之间的相似度来考虑邻域会话。DGRec[28]通过社会关系明确地将不同的用户序列关联起来，但并不是所有的数据都有社会关系属性。此外，THIGE[29]利用时间异构图进行下一项推荐，有效地学习用户和项目的嵌入层次。然而，我们的模型处理序列推荐任务不同于上述方法。与这些模型的详细比较分析将在章节4.5中阐述。

2.2 Dynamic Graph Neural Networks（动态图神经网络）

目前，图神经网络已被用于解决不同的问题，如节点分类[13]、[14]，图嵌入[30]，[31]，图分类[32]，推荐[15]，[16]，[17]，[24]，[25]，[33]等等。

然而，在许多应用中，图数据是随着时间变化的，如学术网络、社交网络、推荐系统等。因此，对动态图进行建模的工作层出不穷。DANE[34]利用矩阵摄动理论在线捕获邻接矩阵和属性矩阵的变化。DynamicTriad[35]采用三元闭合过程来保存动态网络的结构信息和演化模式。DynGEM[36]使用动态扩展的深度自动编码器来捕获高度非线性的图节点的一阶和二阶近似。CTDNE[37]设计了一种基于时间的随机漫步采样方法，用于从连续时间动态网络中学习动态网络嵌入。HTNE[38]将Hawkes过程集成到网络嵌入中，捕捉历史邻居对当前邻居的影响，进行时间网络嵌入。Dyrep[39]利用深度时间点过程模型将结构时间信息编码为低维表示。JODIE[40]利用两种类型的RNN来模拟不同节点表示的演化。MTNE[41]不仅整合了Hawkess过程来激发三和弦的演化过程，而且结合了注意力来区分不同母题的重要性。随着图的发展，为了归纳推断新的节点和观察到的节点的嵌入情况，Xu等人[42]提出了基于经典Bochner定理的时间图注意机制。也有一些作品将动态图裁剪成一系列的快照图。

虽然上述的一些动态推荐方法在电子商务数据集上进行了测试，但它们并不适合序列推荐场景。据我们所知，还没有从动态图的角度来说明序列推荐问题的研究。

3 Preliminaries（预备知识）

在本节中，我们将讨论序列推荐和动态图的问题。

3.1 Sequential Recommendation（序列推荐）

在序列推荐的设置中，设U和I分别表示用户和项目的集合。对于每个用户u ∈ U，其动作序列记为$S^u=(i_1,i_2，\cdot \cdot \cdot ，i_k)$，其中i ∈ I, $T^u=(t_1,t_2，\cdot \cdot \cdot ，t_k)$为$S^u$对应的时间戳序列。所有$S^u$的集合记作S。序列推荐的目标是利用时间$t_k$和$t_k$之前的序列信息预测$S^u$的下一项。一般来说，序列推荐任务将$S^u$的最大长度限制为n。当k大于n时，取最近的n个条目$(i_{k-n},i_{k-n+1}，\cdot \cdot \cdot ，i_k)$进行预测。

每个用户和物品可以分别转换为低维嵌入向量$e_u$, $e_i\in {\mathbb{R}}^d$，其中u ∈ U, i ∈ I, d为嵌入空间的维数。我们使用$E_U\in {\mathbb{R}}^{|U|\times d}$和$E_I\in {\mathbb{R}}^{|I|\times d}$分别表示用户嵌入矩阵和项目嵌入矩阵。

3.2 Dynamic Graph（动态图）

动态图[44]一般分为两类，即离散时间动态图和连续时间动态图。我们的工作主要是指连续时间动态图。

一个动态的网络可以被定义为$G=(V,E,T)$, $V=\{v_1、v_2,\cdot \cdot \cdot ,v_n\}$是节点集和$e\in E$代表$v_i$和$v_j$之间在时间$t\in T$的交互，所以边$e+ij$在$v_i$和$v_j$之间通常是由三联体$(v_i,v_j,t)$。在某些情况下,t也可以表示两个节点之间的交互的顺序。动态图通过记录每条边的时间或顺序，可以捕捉到节点之间关系的演进。动态图嵌入的目的是学习映射函数$f:V\to {\mathbb{R}}^d$，其中d为嵌入维数。

4 Methodology（方法论）

我们现在提出了提出的DGSR模型，其框架如图2所示。该体系结构有四个组成部分:1)动态图构造是将所有用户序列转换为动态图；2)子图抽样是指提取包含用户序列及其相关序列的子图；3)*动态图推荐网络(DGRN)*包含消息传播机制和节点更新部分，从子图中对每个用户偏好进行编码；4)*预测层(predicate Layer)*聚合用户从DGRN学习到的精细化嵌入，并预测下一个项目节点最有可能链接到用户节点。算法2提供了整个框架的伪代码。

图2:DGSR框架概述。以预测$u_1$序列$(i_1,i_2,i_3)$的下一次交互为例。对应的时间戳顺序为$(t_1,t_2,t_3)$。我们首先将$u_1$序列及其相关序列转换为动态图$G^{t_3}$，每条边代表了用户与项目之间的交互，并具有时间属性。虚线表示的边是发生在$t_3$之后的相互作用，这在$G^{t_3}$中没有包含(章节4.1)。然后我们从$G^{t_3}$(章节4.2)中抽样m阶子图$G_{u_1}^m(t3)$。在此基础上，设计良好的动态图推荐网络在不同的用户序列之间传播和聚合信息(章节4.3)。最后，我们将每一层的用户节点嵌入连接起来进行最终的预测(章节4.4)。

4.1 Dynamic Graph Construction（动态图构造）

在这一节中，我们将描述如何将所有的用户序列转换为动态图。当用户u在t时刻对项目i进行操作时，在u和i之间建立一条边e, e可以用五元组表示$(u,i,t,o_u^i,o_i^u)$，t表示交互发生时的时间戳。除此之外，区别于传统动态图的定义，$o_u^i$表示u—i交互的顺序，也就是，第i项在所有与u有交互作用的项目中的位置。$o_i^u$表示与项目i交互的所有用户节点中u的顺序。例如，$u_1$的序列和时间戳序列分别为$(i_1,i_2,i_3)$和$(t_1,t_2,t_3)$。$u_2$的序列和时间戳序列分别为$(i_2,i_3,i_1)$和$(t_4,t_5,t_6)$，其中$t_1<t_2<t_3<t_4<t_5<t_6$。用户和其交互项目的边可以写成$(u_1,i_1,t_1,1,1)$, $(u_1,i_2,t_2,2,1)$、$(u_1,i_3,t_3,3,1)$, $(u_2,i_2,t_4,1,2)$, $(u_2,i_1,t_5,2,2)$和$(u_2,i_3,t_6,3,2)$。

由于大量的用户序列与相同的项交互，例如，如图2所示，$u_1$和$u_2$有共同的项$i_1$和$i_2$, $u_1$和$u_3有$共同的项$i_3$。因此，数据集的所有五元组构成一个动态图，

$$G=\{(u,i,t,o_u^i,o_i^u)|u\in U,i\in V\}$$
除了记录用户与项目交互的时间外，G还记录用户与项目之间的次序信息。因此，我们的动态图比静态图和传统的动态图更适合序列推荐任务。我们定义动态图在时间t中$G^t\in G$，这是一个包含在时间t和t之前的所有用户的交互序列的动态图。对于一个给定的用户序列$S^u=(i_1、i_2,\cdot \cdot \cdot ,i_k)$,对应的时间戳是$T^u=(t_1,t_2,\cdot \cdot \cdot ,t_k)$，预测序列$S^u$的下一项等价于预测$G^{t_k}$中连接到节点u的项目。

4.2 Sub-Graph Sampling（子图采样）

随着用户序列$S^u$的扩展，其邻居序列的数量也在不断增加。同样，由所有用户组成的动态图的规模也在逐渐扩大。这样会增加目标序列的计算量和引入过多的噪声。为了提高训练和推荐的效率，我们提出了一种抽样策略，其细节在算法1中显示。

具体地说,我们首先以用户节点u为锚节点，从$G^{t_k}$图中选择最近的n个一阶邻居,也就是说,与u交互过的的历史项目,写成$N_u$,其中n是用户的最大长度序列(算法1的第5、6和8行)。接下来,对于每一项$i\in N_u$,我们使用它们作为一个锚节点去采样与它们交互过的用户,写成$N_i$(算法1的第11、12和14行)。为了提高抽样效率,我们记录已经被作为锚节点的用户和项目节点，以避免重复抽样(算法1的第7和13行)。其次是类比,可以得到节点u的多跳邻居，这样可以形成$S^u$中用户u的m阶子图$G_u^m(t_k)$（m是超参数，用于控制子图的数量）。

4.3 Dynamic Graph Recommendation Networks（动态图推荐网络，DGRN）

在本节中，我们设计了一个动态图推荐网络(DGRN)，从动态的上下文信息 按照子图$G_u^m(t_k)$ 来对每个用户的偏好进行编码。与绝大多数GNNs相似，DGRN组件包含信息传播组件和节点更新组件。威了便于讨论，我们介绍了DGRN从l—1层到l层的信息传播和节点更新。

消息传播机制的目的是分别学习$G_u^m(t_k)$中从用户到项目和项目到用户的消息传播信息。挑战在于如何分别从用户和项目的角度对邻居的顺序信息进行编码。静态图神经网络，如GCN[13]和GAT[14]，对各种图结构数据具有强大的处理能力。但是，它们不能为每个用户和项目适当地捕获邻居的顺序信息。一些序列模型，如RNN[5]和Transformer [45]net，被广泛用于建模用户的长期和短期兴趣，但它们不能直接处理图结构数据。为此，我们将图神经网络与序列网络相结合，设计了动态传播机制。

**从项目到用户。**用户节点u的邻居节点集合为u已经购买的项目。为了更新每一层的用户节点表示，我们需要从每个用户节点的邻居中提取两种类型的信息，分别是长期偏好和短期偏好。用户的长期偏好[46]反映了用户的固有特征和普遍偏好，可以从用户的所有历史物品中归纳出来。用户的短期偏好反映了他或她最近的兴趣。

**从用户到项目。**项目节点i的邻居节点集合是购买它的用户，其中用户按时间顺序排列。与用户类似，物品的相邻也反映了它的两种类型的特征。一方面，长期特性可以反映物品的一般特性。例如，有钱人通常买高档化妆品。另一方面，短期属性反映了物品的最新属性。例如，许多非体育爱好者也会在世界杯期间购买球衣或球员海报。这部分消费者行为意味着这一时期足球装备的定位已经从职业化向普适性转变。然而，现有的大多数序列推荐方法都不能明确地捕捉到用户节点对项目节点的影响。为了解决这个问题，我们还考虑了从用户到项目的消息传播。

4.3.1 Message Propagation Mechanism（消息传播机制）

在本小节中，我们讨论了DGRN的消息传播机制，包括长期和短期信息的编码。

**长期的信息。**为了从相邻节点中获取节点的长期信息，我们引用了图神经网络和循环神经网络，它们分别明确地考虑了节点与相邻节点的关系和相邻节点的序列依赖性。此外，我们还设计了一种更适合于动态序列推荐的顺序感知注意机制。

• **图卷积神经网络。**GCN[13]是一种直观的方法，直接聚合所有嵌入的邻居节点:

其中$W_1^{(l-1)},W_2^{(l-1)}\in {\mathbb{R}}^{d\ast d}$是编码第l—1层项目和用户的矩阵参数，其中$|N_u|$和$|N_i|$是u和i的邻居节点数。

• **循环神经网络，**如GRU网络，是一种对序列依赖关系进行建模的有效网络。因此，我们利用GRU网络计算用户/物品节点的长期偏好/特征，其计算方法为

其中$(h_{i_1}^{(l-1)},...,h_{i_{|N_u|}}^{(l-1)})$和$(h_{u_1}^{(l-1)},...,h_{u_{|N_u|}}^{(l-1)})$按时间顺序进入GRU。

• **动态图注意力机制。**一般来说，GNN模型关注于显式地捕捉中心节点与相邻节点之间的关系，而忽略了相邻节点之间的序列信息。序列模型正好相反。为了有效区分不同项目的影响，充分利用用户-项目交互的顺序信息，将图注意力机制与序列信息编码相结合，定义了动态注意模块(DAT)。

具体来说，对于每个交互五元组$(u,i,t,o_u^i,o_i^u)$，我们将$r_i^u$定义为项目i相对于用户节点邻居的最后一项的相对顺序，即$r_u^i=|N_u|-o_u^i$。对于每个离散值r，我们指定一个唯一的$p_r^K\in {\mathbb{R}}^d$参数向量作为相对顺序嵌入，对顺序信息进行编码。然后，之间的注意系数$h_u^{(l-1)}$及其邻居节点表示$h_i^{(l-1)}$受$p_{r_i}^K$影响。因此，我们定义了一种相对的顺序感知的注意机制来区分物品对用户的重要性权重$e_{ui}$，拿l-1层节点嵌入$h_u^{(l-1)}$和$h_i^{(l-1)}$作为输入，公式为

其中$h_u^{(0)}$和$h_i^{(0)}$分别是用户嵌入$e_u$和项目嵌入$e_i$。是嵌入的维度，比例系数$\sqrt{d}$是为了避免过大的点积，加快收敛速度。用户与其邻居之间的加权得分通过softmax函数得到:

因此，用户的长期偏好可以通过自适应地聚合其所有邻居的信息来得到:

其中$p_{r_u^i}^V\in {\mathbb{R}}^d$是相对顺序嵌入来捕获用户消息聚合中的顺序信息。类似地，项目的长期特性可以通过以下方式计算:

其中，

且$r_i^u=|N_i|-o_i^u,p_{r_i^u}^V\in {\mathbb{R}}^d$是相对顺序嵌入以捕获项目消息聚合中的顺序信息。

**短期的信息。**在推荐系统中，用户的短期信息反映了用户最近的兴趣爱好，很多作品[12]利用最后一个交互项嵌入作为用户的短期嵌入，但忽略了对历史信息的依赖。为此，我们考虑了注意力机制来模拟最后一次互动与历史互动之间的显着有效性。

• **注意力机制。**我们考虑最后一个项目/用户与每个历史项目/用户之间的注意机制:

其中注意力系数${\alpha }_{ik}$和${\beta }_{uk}$可以这样计算，

其中参数$W_3$和$W_4$∈${\mathbb{R}}^d$，用于控制最后一次交互的权重。

4.3.2 Node updating（节点更新）

在这一阶段，我们将长期嵌入、短期嵌入和前一层嵌入进行聚合去更新$G_u^m(t_k)$节点的表示。

**用户节点更新。**对于用户节点，从第l−1层到第l层的表示更新规则可表示为

其中$W_3^{(l)}\in {\mathbb{R}}^{d\ast 3d}$是控制$h_u^L,h_u^S和h_u^{(l-1)}$信息的用户更新矩阵。

**项目节点更新。**类似地，项目表示更新规则是

其中$W_4^{(l)}\in {\mathbb{R}}^{d\ast 3d}$是控制$h_i^L,h_i^S和h_i^{(l-1)}$信息的项目更新矩阵。

4.4 Recommendation and Optimization（推荐与最优化）

在我们的模型中，预测$S_u=(i_1,i_2，\cdot \cdot \cdot ，i_k)$的下一次交互相当于预测子图$G_u^m(t_k)$的用户节点u的链接。在本小节中，我们设计了链接预测函数，以确定用户接下来可能与之交互的项目。

将L层DGRN作用于$G_u^m(t_k)$后，得到节点u的多重嵌入$(h_u^{(0)},h_u^{(1)},...,h_u^{(L)})$，其中包含每一层用户嵌入$h_u^{(l)}$。用户嵌入在不同的层强调不同的用户偏好[3]。因此，我们将用户多次嵌入连接起来，得到节点u的最终嵌入:

对于给定的候选项i ∈ I，链接函数定义为：

其中向量$s_{ui}=(s_{u1},s_{u2}，\cdot \cdot \cdot ，s_{u|I|})$表示u对每个候选项的得分向量。$W_P\in {\mathbb{R}}^{(L+1)d\times d}$是可训练的变换矩阵。

为了学习模型参数，我们优化了交叉熵损失。用户u对候选项得分的归一化向量为

目标函数如下:

其中$y_u$为$S^u$下一次交互的ground truth项目的独热编码向量，Θ为所有模型参数，$\Vert \cdot {\Vert }_2$为L2范数。λ是控制正则化强度。

4.5 Model Discussions（模型讨论）

本小节将我们的DGSR与一些有代表性的序列推荐模型进行比较和分析。

一些编码用户偏好的序列模型仅依赖于其内部序列，而不显式利用其他序列信息，如TiSASRec[23]、SR-GNN和HGN[47]，可以看作是我们DGSR的特例。具体来说，在一层DGRN网中，我们可以在项目→用户的消息传播机制中，用一些复杂的网络、自注意网络、GGNN网络或门控网络来代替我们当前的设置，并禁用作为u最终偏好表示的消息。因此，作为一个新的框架，我们的模型可以通过修改消息传播机制部分来融合几乎所有的单序列模型。

还有一些模型[26]、[27]、[29]，它们是为了利用交叉序列信息或捕获不同序列之间的项关系而设计的。但是，与DGSR相比，它们有很多不同和局限性。例如，CSRM[27]通过直接计算邻域序列与目标序列的相似度来考虑邻域序列，但没有利用用户的细粒度交互信息，包括每一项与与之交互的所有用户之间的交互顺序。与之相比，我们的模型基于良好的消息传播机制度量不同序列之间的相似性，提高了用户与项目之间的交互利用率。HyperRec[26]采用超图来关联每个周期内项目之间的高阶相关连接。尽管如此，超图是一种粗糙的建模用户-物品交互的方法，它导致许多精细化的信息被忽略了，例如每个交叉序列中显式的顺序信息。我们的DGSR构造的动态图可以更多灵活地表示更丰富的交互信息。在社交推荐中，DGRec[28]通过社交属性信息明确关联不同的用户序列，但在序列推荐场景中，并非所有数据都具有社交关系属性。我们的模型也可以显式地关联不同的用户序列，而不依赖于其他辅助信息。

5 Experiments（实验）

在本节中，我们将在三个真实的数据集上进行实验，以评估我们的模型的性能。我们旨在通过实验回答以下问题。

• RQ1:与最先进的序列推荐方法相比，DGSR的表现如何?
• RQ2:动态图推荐网络组件在DGSR中的有效性如何?
• RQ3:不同的超参数设置(DGRN层数、子图采样大小、最大序列长度、嵌入大小)对DGSR的影响是什么?

5.1 Datasets（数据集）

为了评估我们的模型的有效性，我们对来自真实平台[48]的三个Amazon数据集（http://jmcauley.ucsd.edu/data/amazon）进行了实验:Amazon- cd、Amazon- games和Amazon- Beauty。这些数据集被广泛应用于评价序列推荐方法，并且在领域、大小和稀疏性方面各不相同。

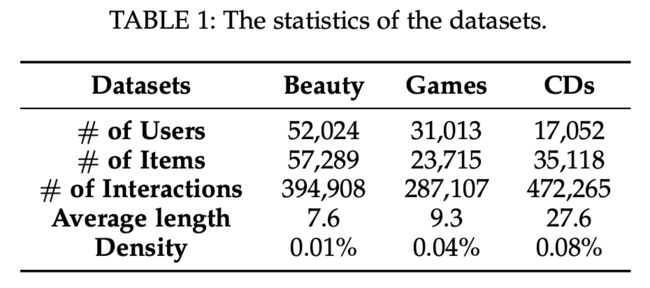
所有这些数据集都包含时间戳或交互的特定日期。对于所有数据集，我们将评论或评级的出现视为隐含的反馈，并丢弃相关操作少于5个的用户和项目[11]。处理后的数据统计如表1所示。对于每个用户序列，我们使用最近的项进行测试，使用第二个最近的项进行验证，其余的项用于训练集。为了充分捕获动态协作信号，我们将每个序列$S^u$分割成一系列序列和标签。例如,对于一个输入,$S^u=(i_1,i_2,i_3,i_4)$和$T^u=(t_1,t_2,t_3,t_4)$我们生成序列和标签$[i_1]\to i_2$, $[i_1,i_2]\to i_3$和$[i_1,i_2,i_3]\to i_4$。然后，对应的子图和被链接的节点分别为$(G_u^m,(t_1)，i2)，(G_u^m,(t_2)，i3))和(G_u^m,(t_3)，i4)$。这些处理可以在训练和测试之前进行。

5.2 Experiment Settings（实验设置）

5.2.1 Compared Methods（比较方法）

为了证明其有效性，我们将我们提出的DGSR方法与以下方法进行了比较:

• BPR-MF[49]，基于矩阵分解的模型，从用户隐式反馈中学习两两个性化排名。
• FPMC[4]，一个结合矩阵分解和一阶马尔可夫链的模型，以捕捉用户的长期偏好和项目到项目的转换。
• GRU4Rec+[7]，改进的基于RNN的模型，对Top-K推荐采用不同的损失函数和采样策略。
• Caser[10]，一种基于CNN的模型，通过对L近期项的嵌入进行卷积运算来捕获高阶马尔可夫链。
• SASRec[11]，基于自我注意力的模型，识别相关项目，预测下一个项目。
• SR-GNN[15]，一个基于GNN的模型，用于捕获项目的复杂转换关系，用于基于会话的推荐。
• HGN[47]，序列模型，包含特征门控、实例门控和实例门控模块，以选择重要的特征并显式捕获项目关系。
• TiSASRec[23]，基于间隔感知的自我注意模型，将绝对位置和它们之间的时间间隔按顺序建模。
• HyperRec[26]，一种基于超图的模型，该模型采用超图来捕获项目之间的多阶连接，用于下一项推荐。

5.2.2 Evaluation Metrics（评估指标）

我们采用两个广泛使用的度量标准[11]Hit@K和NDCG@K来评价所有方法。Hit@K表示ground-truth项目在top@K项目中的比例，而NDCG@K是位置感知的度量，以及更高的位置。在[11]，[23]之后，对于每个测试样本，我们随机抽取100个负面项目，并将这些项目与基本事实项目进行排序。我们根据这101个项目评估Hit@K和NDCG@K。默认情况下，我们设置K =10。

5.2.3 Parameter Setup（参数设置）

我们在DGL Library（https://www.dgl.ai）[50]中实现了我们的DGSR模型。对于所有方法，嵌入大小固定为50。最大序列长度n设置为50。优化器为Adam优化器[51]，学习速率设置为0.01。批量大小为50。λ是1e-4。我们设置子图抽样m的顺序为4。DAN层数L在Beauty和CDs设置为3，在Games设置为2。我们用不同的随机种子进行了四次评估，并报告了每种方法的平均值。对于比较的方法，对于对比方法，我们使用默认的超参数。所有的实验都是在一台装有8个NVIDIA GeForce RX2080Ti (11GB)和4个Intel Xeon E5-2660 v4处理器的计算机服务器上进行的。

5.3 Performance Comparison (RQ1)（表现比较）

我们首先报告所有方法的性能。表2总结了性能比较结果。可以得到以下观察结果:

• DGSR在三个数据集与大多数评估指标上取得了最好的性能。特别是，在Beauty、Games和CDs中，DGSR比最强基线w.r.t NDCG@10分别提高了10.56%、3.92%、3.81%。值得注意的是，Beauty是最稀疏和最短的数据集，所以许多用户和项目只有很少的交互。在我们的模型中，动态图的高阶连通性缓解了这个问题。因此，Beauty有了显著的改进。通过DGRN层的叠加，DGSR可以明确地利用交叉序列信息，为预测提供更多的辅助信息。而TiSASRec、HGN、SR- GNN和SASRec仅将每个序列独立编码为用户的动态兴趣表示。值得注意的是，HyperRec利用了许多相关的用户交互信息，但其表现却不如我们的DGSR，特别是在Beauty和Games方面。我们认为这是由于HyperRec忽略了细化相关用户序列的交互顺序信息。与CDs相比，Beauty和Games具有更强的序列特性，因此DGSR在Beauty和Games上的性能明显优于HyperRec。
• SASRec、HGN、SR-GNN和TiSASRec的性能优于神经方法GRU4Rec+和Caser。一个可能的原因是，他们可以通过使用注意力或分级门控机制显式地捕获项目-项目关系。在大多数情况下，Caser通常比GRU4Rec+获得更好的性能。这种改进可能归功于CNN模块，它可以捕获比GRU网络更复杂的行为模式。SR-GNN在基于会话的推荐场景中具有良好的性能，而在序列推荐场景中则表现平平。一个可能的原因是我们的数据缺乏重复性，使得用户序列很难形成图结构。
• BPR-MF在三个数据集上的性能都很差。由于BPR-MF只能捕捉用户的一般兴趣，对用户的行为序列进行建模具有挑战性。GRU4Rec+在Beauty和Games中的表现略低于FPMC，而在CDs中的表现更好。原因可能是FPMC专注于项目的动态转换，因此它们在稀疏数据集[23]上表现得更好。

5.4 Study of Dynamic Graph Recommendation Networks (RQ2)（动态图推荐网络的研究）

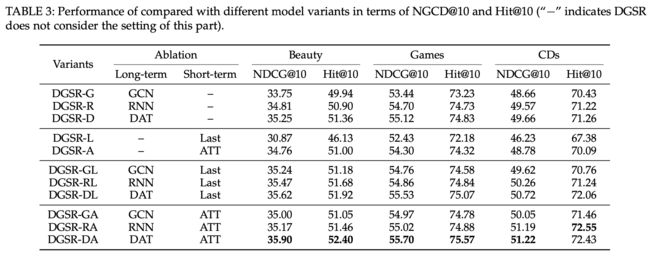
为了研究DGRN组件在DGSR中的优势，我们将不同变体的DGSR在Games、Beauty和CDs数据集上进行比较，这些数据集设置了用于编码长期和短期信息的不同模块。表3显示了各变量模型及其结果，结果如下:

• 在Games和CDs数据集上，DGSR-D优于DGSR-R和DGSR-G。我们将注意力机制和相对顺序嵌入相结合，可以充分提取每个节点邻居的长期信息。DGSR-R在Beauty中取得了具有竞争力的成绩。这可能是由于序列长度较小，GRU网可以像动态注意模块一样对序列的依赖性进行建模。基于GCN的变体在三个数据集上都取得了较差的性能。这可能是因为GCN模块将所有邻居节点都视为同等重要，从而在消息传播过程中引入了更多的噪声。DGSR-A的性能也优于DGSR-L。验证了仅利用最后一次交互嵌入不足以捕获短期信息。
• 所有带有两个模块(长期和短期)的变体始终优于单模块(长期或短期)的变体。它说明了结合长期和短期信息的必要性。虽然DGSR-R在Beauty中的表现优于DGSR-D，但DGSR-DA优于DGSR-RA和DGSR-RL。一个可能的原因是DGSR-DA考虑了中心节点与邻居节点之间的关系，有利于信息在动态图中传播。而DGSR-RL和DGSR-RA只关注邻居间的相互作用，忽略了中心节点的作用。

5.5 The Sensitivity of Hyper-parameters (RQ3)（超参数的敏感性）

为探讨用户序列间动态协作信息显式建模对DGSR性能的影响，研究了DGRN层数l、子图顺序和用户序列最大长度n三个超参数对DGSR性能的影响。

5.5.1 Effect of DGRN Layer numbers（DGRN层数的影响）

我们在Games和Beauty数据集上使用不同的DGRN层数l来进行我们的方法。DGSR-0表示只使用用户嵌入和最后一个项目嵌入进行推荐。DGSR-1表示单层DGRN，表示仅利用序列内信息进行预测。DGSR-l (l>1)表示DGSR可以利用l阶用户序列信息进行预测。从图3可以看出:

• 增加DGSR层能够大幅提升性能。结果表明，利用高阶用户序列信息可以有效地提高推荐性能。DGSR-2和DGSR-3分别在Games和Beauty比赛中获得最佳成绩。一个可能的原因是，Beauty比Games更稀疏，可能需要更多层次来引入更多上下文信息。
• 当进一步叠加传播层时，我们发现DGSR-3和DGSR-4的性能开始变差。原因可能是使用更多的传播层会导致过度平滑，这也与[52]中的发现一致。
• DGSR-1在所有情况下始终优于DGSR-0，甚至优于大多数基线。动态图推荐网络中消息传播机制的强大，可以有效地将用户序列中的顺序信息编码到额外的用户动态偏好中。

5.5.2 Effect of the sub-graph sampling size（子图抽样大小的影响）

我们用不同的子图样本大小来执行我们的方法。子图m的顺序决定了抽样的大小。特别地，我们在{1,2,3,4}范围内搜索m。从图4的结果可以看出，当m从1增加到3时，可以有效地提高模型性能。其原因是，更大尺寸的子图可以为每个用户序列提供更动态的上下文信息，以帮助预测。随着m的增加，由于DGRN层数的限制，模型性能趋于稳定。在实际操作中，我们不能盲目地增大m的值，因为子图的大小会随着m的增大而呈指数增长，这样会导致我们训练或测试卡住。

5.5.3 Effect of the maximum sequence length（最大序列长度的影响）

我们在n从10到60的Games和Beauty数据集上训练和测试我们的方法，同时保持其他最优超参数不变。此外，为了进一步研究明确利用动态协同信息的好处，我们还对不同n进行了DGSR-1。Hit@10的结果如图5所示。我们有以下发现:

• 将DGSR的n从10增加到50，持续提高游戏数据的性能。当n设置为20和50时，DGSR在Beauty上表现更好。但是，盲目增加n并不一定能提高DGSR和DGSR-1的性能。它很可能带来噪声，导致性能下降。
• 与DGSR-1相比，在n的各个取值处，DGSR的表现都优于DGSR-1。具体而言,即使n设置为10,DGSR仍比DGSR-1的最佳性能,这意味着明确利用用户序列的高阶上下文信息可以缓解用户历史信息不足的问题，从而提高推荐性能。

5.5.4 Effect of the embedding size（嵌入大小的影响）

在此基础上，进一步分析了不同维数的嵌件对研究结果的影响。图6描述了嵌入尺寸为16 ~ 80时模型的性能。可以看出，随着维数的增加，模型的性能逐渐提高。随着维数的进一步增加，性能趋于稳定。这验证了我们的模型在不同维度上的稳定性。

6 Conclusion（结论）

本工作探讨了在序列推荐中显式地建模不同用户序列之间的动态协作信息。受动态图神经网络的启发，我们提出了一种新的方法DGSR。在DGSR中，所有用户序列都被转换成一个动态图，其中包含了用户-项目交互的时间顺序和时间戳。DGSR的关键是设计良好的动态图推荐网络，实现了对不同用户序列之间的动态协作信息进行显式编码。最后将下项预测任务转换为动态图的节点-链接预测，对模型进行端到端训练。在三个真实数据集上的大量实验验证了DGSR算法的有效性和合理性。

Reference（参考文献）

[1] B. Sarwar, G. Karypis, J. Konstan, and J. Riedl, “Item-based collaborative filtering recommendation algorithms,” in Proceedings of the 10th international conference on World Wide Web, 2001, pp. 285–295.
[2] X. He, L. Liao, H. Zhang, L. Nie, X. Hu, and T.-S. Chua, “Neural collaborative filtering,” in Proceedings of the 26th international conference on world wide web, 2017, pp. 173–182.
[3] X. Wang, X. He, M. Wang, F. Feng, and T.-S. Chua, “Neural graph collaborative filtering,” in Proceedings of the 42nd international ACM SIGIR conference on Research and development in Information Retrieval, 2019, pp. 165–174.
[4] S. Rendle, C. Freudenthaler, and L. Schmidt-Thieme, “Factorizing personalized markov chains for next-basket recommendation,” in Proceedings of the 19th international conference on World wide web, 2010, pp. 811–820.
[5] B. Hidasi, A. Karatzoglou, L. Baltrunas, and D. Tikk, “Sessionbased recommendations with recurrent neural networks,” arXiv preprint arXiv:1511.06939, 2015.
[6] M. Quadrana, A. Karatzoglou, B. Hidasi, and P. Cremonesi, “Personalizing session-based recommendations with hierarchical recurrent neural networks,” in Proceedings of the Eleventh ACM Conference on Recommender Systems, 2017, pp. 130–137.
[7] B. Hidasi and A. Karatzoglou, “Recurrent neural networks with top-k gains for session-based recommendations,” in Proceedings of the 27th ACM International Conference on Information and Knowledge Management, 2018, pp. 843–852.
[8] H. Sak, A. W. Senior, and F. Beaufays, “Long short-term memory recurrent neural network architectures for large scale acoustic modeling,” 2014.
[9] J. Chung, C. Gulcehre, K. Cho, and Y. Bengio, “Empirical evaluation of gated recurrent neural networks on sequence modeling,” arXiv preprint arXiv:1412.3555, 2014.
[10] J. Tang and K. Wang, “Personalized top-n sequential recommendation via convolutional sequence embedding,” in Proceedings of the Eleventh ACM International Conference on Web Search and Data Mining, 2018, pp. 565–573.
[11] W.-C. Kang and J. McAuley, “Self-attentive sequential recommendation,” in 2018 IEEE International Conference on Data Mining (ICDM). IEEE, 2018, pp. 197–206.
[12] Q. Liu, Y. Zeng, R. Mokhosi, and H. Zhang, “Stamp: short-term attention/memory priority model for session-based recommendation,” in Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 2018, pp. 1831– 1839.
[13] T. N. Kipf and M. Welling, “Semi-supervised classification with graph convolutional networks,” in 5th International Conference on Learning Representations, ICLR 2017. OpenReview.net, 2017.
[14] P. Velickovic, G. Cucurull, A. Casanova, A. Romero, P. Lio`, and Y. Bengio, “Graph attention networks,” in 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, April 30 - May 3, 2018, Conference Track Proceedings. OpenReview.net, 2018.
[15] S. Wu, Y. Tang, Y. Zhu, L. Wang, X. Xie, and T. Tan, “Session-based recommendation with graph neural networks,” in Proceedings of the AAAI Conference on Artificial Intelligence, vol. 33, 2019, pp. 346– 353.
[16] M. Zhang, S. Wu, M. Gao, X. Jiang, K. Xu, and L. Wang, “Personalized graph neural networks with attention mechanism for session-aware recommendation,” IEEE Transactions on Knowledge and Data Engineering, 2020.
[17] R. Qiu, J. Li, Z. Huang, and H. Yin, “Rethinking the item order in session-based recommendation with graph neural networks,” in Proceedings of the 28th ACM International Conference on Information and Knowledge Management, 2019, pp. 579–588.
[18] R. Trivedi, M. Farajtabar, P. Biswal, and H. Zha, “Dyrep: Learning representations over dynamic graphs,” in International Conference on Learning Representations, 2018.
[19] R. He and J. McAuley, “Fusing similarity models with markov chains for sparse sequential recommendation,” in 2016 IEEE 16th International Conference on Data Mining (ICDM). IEEE, 2016, pp. 191–200.
[20] R. He, W.-C. Kang, and J. McAuley, “Translation-based recommendation,” in Proceedings of the eleventh ACM conference on recommender systems, 2017, pp. 161–169.
[21] F. Yu, Q. Liu, S. Wu, L. Wang, and T. Tan, “A dynamic recurrent model for next basket recommendation,” in Proceedings of the 39th International ACM SIGIR conference on Research and Development in Information Retrieval, 2016, pp. 729–732.
[22] J. Li, P. Ren, Z. Chen, Z. Ren, T. Lian, and J. Ma, “Neural attentive session-based recommendation,” in Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, 2017, pp. 1419–1428.
[23] J. Li, Y. Wang, and J. McAuley, “Time interval aware self-attention for sequential recommendation,” in Proceedings of the 13th International Conference on Web Search and Data Mining, 2020, pp. 322–330.
[24] C. Xu, P. Zhao, Y. Liu, V. S. Sheng, J. Xu, F. Zhuang, J. Fang, and X. Zhou, “Graph contextualized self-attention network for sessionbased recommendation,” in IJCAI, 2019, pp. 3940–3946.
[25] C. Ma, L. Ma, Y. Zhang, J. Sun, X. Liu, and M. Coates, “Memory augmented graph neural networks for sequential recommendation,” in The Thirty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2020. AAAI Press, 2020, pp. 5045–5052.
[26] J. Wang, K. Ding, L. Hong, H. Liu, and J. Caverlee, “Next-item recommendation with sequential hypergraphs,” in Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, 2020, pp. 1101–1110.
[27] M. Wang, P. Ren, L. Mei, Z. Chen, J. Ma, and M. de Rijke, “A collaborative session-based recommendation approach with parallel memory modules,” in Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval, 2019, pp. 345–354.
[28] W. Song, Z. Xiao, Y. Wang, L. Charlin, M. Zhang, and J. Tang, “Session-based social recommendation via dynamic graph attention networks,” in Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining, 2019, pp. 555–563.
[29] Y. Ji, M. Yin, Y. Fang, H. Yang, X. Wang, T. Jia, and C. Shi, “Temporal heterogeneous interaction graph embedding for nextitem recommendation,” 2020.
[30] J. Tang, M. Qu, M. Wang, M. Zhang, J. Yan, and Q. Mei, “Line: Large-scale information network embedding,” in Proceedings of the 24th international conference on world wide web, 2015, pp. 1067–1077.
[31] B. Perozzi, R. Al-Rfou, and S. Skiena, “Deepwalk: Online learning of social representations,” in Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining, 2014, pp. 701–710.
[32] H. Gao and S. Ji, “Graph u-nets,” in Proceedings of the 36th International Conference on Machine Learning, ICML 2019, 9-15 June 2019, Long Beach, California, USA, ser. Proceedings of Machine Learning Research, K. Chaudhuri and R. Salakhutdinov, Eds., vol. 97. PMLR, 2019, pp. 2083–2092. [Online]. Available: http://proceedings.mlr.press/v97/gao19a.html
[33] X. Li, M. Zhang, S. Wu, Z. Liu, L. Wang, and P. S. Yu, “Dynamic graph collaborative filtering,” in 2020 IEEE International Conference on Data Mining (ICDM), 2020, pp. 322–331.
[34] J. Li, H. Dani, X. Hu, J. Tang, Y. Chang, and H. Liu, “Attributed network embedding for learning in a dynamic environment,” in Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, 2017, pp. 387–396.
[35] L. Zhou, Y. Yang, X. Ren, F. Wu, and Y. Zhuang, “Dynamic network embedding by modeling triadic closure process,” 32nd AAAI Conference on Artificial Intelligence, AAAI 2018, pp. 571–578, 2018.
[36] P. Goyal, N. Kamra, X. He, and Y. Liu, “Dyngem: Deep embedding method for dynamic graphs,” arXiv preprint arXiv:1805.11273, 2018.
[37] G. H. Nguyen, J. B. Lee, R. A. Rossi, N. K. Ahmed, E. Koh, and S. Kim, “Continuous-Time Dynamic Network Embeddings,” The Web Conference 2018 - Companion of the World Wide Web Conference, WWW 2018, no. BigNet, pp. 969–976, 2018.
[38] Y. Zuo, J. Guo, G. Liu, X. Hu, H. Lin, and J. Wu, “Embedding temporal network via neighborhood formation,” Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 2857–2866, 2018.
[39] R. Trivedi, M. Farajtabar, P. Biswal, and H. Zha, “Dyrep: Learning representations over dynamic graphs,” in 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, May 6-9, 2019. OpenReview.net, 2019.
[40] S. Kumar, X. Zhang, and J. Leskovec, “Predicting dynamic embedding trajectory in temporal interaction networks,” in Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 2019, pp. 1269–1278.
[41] H. Huang, Z. Fang, X. Wang, Y. Miao, and H. Jin, “Motifpreserving temporal network embedding,” in Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, IJCAI-20, pp. 1237–1243.
[42] D. Xu, C. Ruan, E. Korpeoglu, S. Kumar, and K. Achan, “Inductive representation learning on temporal graphs,” arXiv preprint arXiv:2002.07962, 2020.
[43] A. Sankar, Y. Wu, L. Gou, W. Zhang, and H. Yang, “Dysat: Deep neural representation learning on dynamic graphs via selfattention networks,” in Proceedings of the 13th International Conference on Web Search and Data Mining, 2020, pp. 519–527.
[44] S. M. Kazemi, R. Goel, K. Jain, I. Kobyzev, A. Sethi, P. Forsyth, and P. Poupart, “Representation learning for dynamic graphs: A survey.” Journal of Machine Learning Research, vol. 21, no. 70, pp. 1–73, 2020.
[45] A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. Kaiser, and I. Polosukhin, “Attention is all you need,” arXiv preprint arXiv:1706.03762, 2017.
[46] Z. Yu, J. Lian, A. Mahmoody, G. Liu, and X. Xie, “Adaptive user modeling with long and short-term preferences for personalized recommendation.” in IJCAI, 2019, pp. 4213–4219.
[47] C. Ma, P. Kang, and X. Liu, “Hierarchical gating networks for sequential recommendation,” in Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 2019, pp. 825–833.
[48] J. McAuley, C. Targett, Q. Shi, and A. Van Den Hengel, “Imagebased recommendations on styles and substitutes,” in Proceedings of the 38th international ACM SIGIR conference on research and development in information retrieval, 2015, pp. 43–52.
[49] S. Rendle, C. Freudenthaler, Z. Gantner, and S. Lars, “Bpr: Bayesian personalized ranking from implicit feedback. uai’09,” Arlington, Virginia, United States, pp. 452–461, 2009.
[50] M. Wang, L. Yu, D. Zheng, Q. Gan, Y. Gai, Z. Ye, M. Li, J. Zhou, Q. Huang, C. Ma, Z. Huang, Q. Guo, H. Zhang, H. Lin, J. Zhao,
J. Li, A. J. Smola, and Z. Zhang, “Deep graph library: Towards efficient and scalable deep learning on graphs,” ICLR Workshop on Representation Learning on Graphs and Manifolds, 2019.
[51] D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” Computer Science, 2014.
[52] Q. Li, Z. Han, and X.-M. Wu, “Deeper insights into graph convolutional networks for semi-supervised learning,” in Thirty-Second AAAI Conference on Artificial Intelligence, 2018.