多智能体强化学习- COMA

COMA：Counterfactual Multi-Agent Policy Gradients

论文地址：https://arxiv.org/pdf/1705.08926.pdf

代码地址：https://github.com/oxwhirl/pymarl/tree/master/

摘要

本文提出一种多主体的actor-critic，称为反事实多主体策略梯度（COMA）。文章采用CTED的训练方式。利用反事实基线来解决多智能体的信用分配问题。文章的主要思想：
1:使用一个集中的critic，在训练的时候获取所有智能体的信息（on-policy）
2:反事实基线：解决信用分配问题
3.critic网络对反事实基线进行高效计算。

方法

作者是基于Actor-Critic结构来设计MARL算法的。最直接的方法是每个智能体利用该结构独立学习，称作independent actor-critic (IAC)。但是IAC有个明显的问题，就是不考虑其它智能体的信息，这将导致训练过程不稳定。（如果IAC在训练的过程中考虑所有智能体的信息，利用CTDE训练方法，则和MADDPG方法没有太大区别）。

首先，COMA使用了一个集中的Critic，critic以全局状态s或者所有智能体的联合行动-观测历史$\tau$作为输入.

（信用分配问题）在协作任务下的多智能体系统中，奖励函数是全局共享的，所以只需要一个critic网络就可以了。但是那样的话，所有的智能体优化目标都是同一个。因此，对每个actor网络来说，从critic那边反向传播过来的误差都是一样的。令每个智能体直接利用该集中式的critic计算策略梯度可以得到：
$$g={\nabla }_{{\theta }^{\pi }}log\pi (u|{\tau }_t^a)(r+\gamma V(s_t+1)-V(s_t))$$

这种“吃大锅饭”式的训练方式显然不是最有效的，因为每个actor网络对整体性能的贡献不一样，贡献大的反向传播的误差应该要稍微小些，贡献小的其反向传播误差应该要大一些。最终的目标都是优化整体的性能。所以，受到差分奖励的影响，作者提出利用counterfactual baseline来解决该问题！
在差分奖励中，每个智能体的奖励设计为：
$$D^{\alpha }=r(s,u)-r(s,(u^{-a},c^a))$$
即全局奖励减当智能体a的动作替换为默认动作$c^a$时全局奖励的差值。a代表智能体，u表示动作，-a表示除a以外的智能体集合。
这个方法的问题在于：需要大量模拟环境去评估不同智能体的$r(s,(u^{-a},c^a)$，同时，需要认为设定默认动作作$c^a$。COMA利用一个集中的critic来解决这个问题。
集中式的critic计算$Q(s,u)$（联合动作u的Q值估计），对于每一个智能体a，计算一个优势函数，将当前动作$u^a$的Q值与保持其他智能体动作$u^{-a}$不变单独边缘化$u^a$之后所对应的期望Q值的差值：
$$A^a(s,u)=Q(s,u)-\sum _{u^{\prime }a}{\pi }^a(u^{{}^{\prime }a}|{\tau }^a)Q(s,(u^{-a},u^{\prime a}))$$
$A^a(s,u)$为每个智能体计算一个单独的基准来推测只有a的动作变化时会发生什么，该方法直接通过智能体的经验学习得到，而无需依赖额外的仿真，单独的奖励模型或者认为设计的默认动作。这里的反事实基准就是$b(s)={\pi }^a(u^{{}^{\prime }a}|{\tau }^a)Q(s,(u^{-a},u^{\prime a}))$实际上就是基准$b(s)$，$A^a(s,u)$就是$G_t-b(s)$，它的作用是进行梯度上升操作，因此该方法的基础就是带基准的策略梯度算法。相当于在多智能体系统中，r是系统奖励，$Q(u,a)$ 是系统奖励对应的Q值，难以反映单个智能体对系统的贡献，而通过减去一个基准值之后得到的 $A^a(s,u)$ 却能够反映单个智能体的Q值，并且不会改变策略梯度的值.
利用critic表征对反事实基准进行高效估计：${\pi }^a(u^{{}^{\prime }a}|{\tau }^a)Q(s,(u^{-a},u^{\prime a}))$的估计需要大量的计算，另外，网络的输出节点等于联合动作空间的大小$U^n$，为了解决这个问题，COMA提出一种新的critic表征方法。

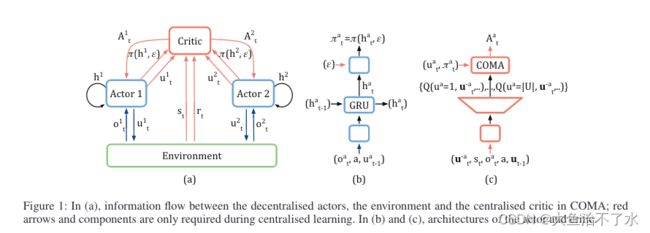
如图（c）所以，每一时刻，将其他智能体的动作$u_t^{-a}$作为网络输入的一部分，输出是智能体a的所有可能动作的Q值，这样，只需要对每个智能体进行一次单独的actor和critic的前向计算，就能够高效的得到优势函数。输出节点的数量从$U^n$变成了$U$。
另外，本文考虑的是离散动作，实际上COMA能够轻易地扩展到连续动作空间中，此时只需要利用蒙特卡洛方法计算优势函数中的期望，或者使用函数形式，使其可分析。

实验部分

实验环境，StarCraft,