机器学习-作业（一）-python求解兵王问题

数据集下载位置

Index of /ml/machine-learning-databases/chess/king-rook-vs-king

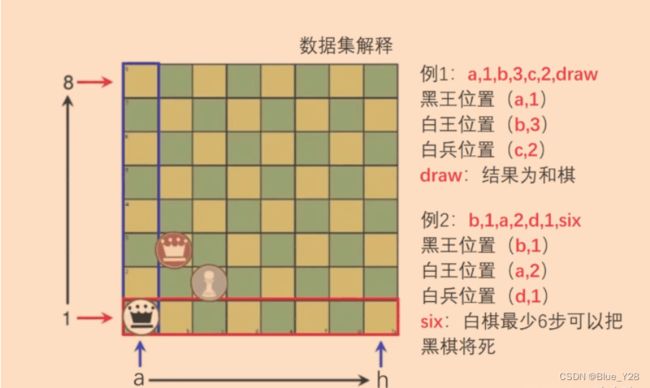
数据简单介绍

数据处理

#加载数据
class Krkoptdataset(Dataset):
    def __init__(self):
        #读取数据
        xy = pd.read_csv('../datafile/krkopt.data')
        #增加表头
        xy.columns = ['bk_x','bk_y','wk_x','wk_y','ws_x','ws_y','outcome']
        #数据格式化
        xy.replace(to_replace={'^a$': 1, '^b$': 2, '^c$': 3, '^d$': 4, '^e$': 5, '^f$': 6, '^g$': 7, '^h$': 8, '^draw$': 1,
                    "(?!draw)": 0}, regex=True, inplace=True)
        #数据归一化
        xy[['bk_x','bk_y','wk_x','wk_y','ws_x','ws_y']] = preprocessing.scale(
            xy[['bk_x','bk_y','wk_x','wk_y','ws_x','ws_y']])
        pd.DataFrame(data=xy).to_csv("krkopt_fill.csv")
        new_xy = pd.read_csv('krkopt_fill.csv')

        self.x_data = new_xy[['bk_x','bk_y','wk_x','wk_y','ws_x','ws_y']]
        self.y_data = new_xy[['outcome']]
        self.len = new_xy.shape[0]

    def __getitem__(self, item):

        return self.x_data[item],self.y_data[item]

    def __len__(self):

        return self.len

    def getX(self):

        return self.x_data

    def getY(self):

        return self.y_data

分割数据：交叉验证法

krkopt = Krkoptdataset()

X_train, X_test, y_train, y_test = train_test_split(krkopt.getX(),krkopt.getY(), train_size=5000, random_state=0)

训练模型

我们需要在和中找出识别率最高的c和gamma

粗略设定超参数

#先随意设定一个c和gamma看一下训练的结果
clf = svm.SVC(C=10, tol=1e-3, gamma=0.8, kernel='rbf', decision_function_shape='ovr', probability=True)
clf.fit(X_train,y_train)
score2 = clf.score(X_test, y_test)
print("test score:{}".format(score2))

#先粗略的找到c和gamma的值
C=[]
gamma=[]
for cs in range(-5,15,2):
    C.append(2**cs)
for gs in range(-15,3,2):
    gamma.append(2**gs)


clf = svm.SVC(tol=1e-3, kernel='rbf', decision_function_shape='ovr', probability=True)

tuned_parameters={"gamma": gamma, "C": C}
clf = GridSearchCV(svm.SVC(), tuned_parameters, n_jobs=-1,cv=5)
clf.fit(X_train, y_train)

print("Best parameters set found on development set:")

print(clf.best_params_)
print(clf.best_score_)

Best parameters set found on development set:

0.9943613099110822
{'C': 128, 'gamma': 0.125}

进一步缩小范围查找c和gamma的值

newC = np.linspace((32+128)/2,(128+512)/2,10)
newGamma = np.linspace((0.03125+0.125)/2,(0.125+0.5)/2,10)
clf = svm.SVC(tol=1e-3, kernel='rbf', decision_function_shape='ovr', probability=True)

tuned_parameters={"gamma": newGamma, "C": newC}
clf = GridSearchCV(svm.SVC(), tuned_parameters, n_jobs=5,cv=5)
clf.fit(X_train, y_train)

print("Best parameters set found on development set:")

print(clf.best_params_)
print(clf.best_score_)

Best parameters set found on development set:

{'C': 106.66666666666667, 'gamma': 0.18229166666666669}
0.9945999999999999

超参数的优化步骤

1. 设定超参数的范围（这里的c和gamma已经有范围）
2. 从设定的超参数范围中随机采样（比如这里由于c和gamma的范围是2的阶乘，所以以对数尺度指定范围）
3. 通过学习得到识别度
4. 重复2,3步骤，根据识别精度，缩小超参数范围

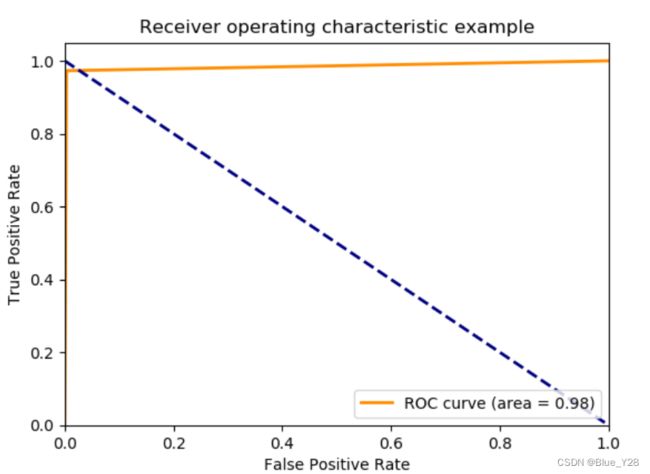
结果评估

#绘图代码
fpr,tpr,threshold = roc_curve(y_test, y_pre) ###计算真正率tp和假正率fp
roc_auc = auc(fpr,tpr) ###计算auc的值，auc就是曲线包围的面积，越大越好
lw = 2
plt.figure(figsize=(10,10))
plt.plot(fpr, tpr, color='darkorange',lw=lw, label='ROC curve (area = %0.2f)' % roc_auc) ###假正率为横坐标，真正率为纵坐标做曲线
plt.plot([0, 1], [1, 0], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()