Chapter6：Logistics 回归：AndrewNg吴恩达《机器学习》笔记

6.1 Logistic Regression是一种分类算法

• 在分类问题中，你要预测的变量 $y$ 是离散的值，我们将学习一种叫做逻辑回归 (Logistic Regression) 的算法，这是目前最流行使用最广泛的一种学习算法。

• 三个分类问题的例子：

​ 恰巧这三个问题都属于二分类问题，当然还有多分类问题。

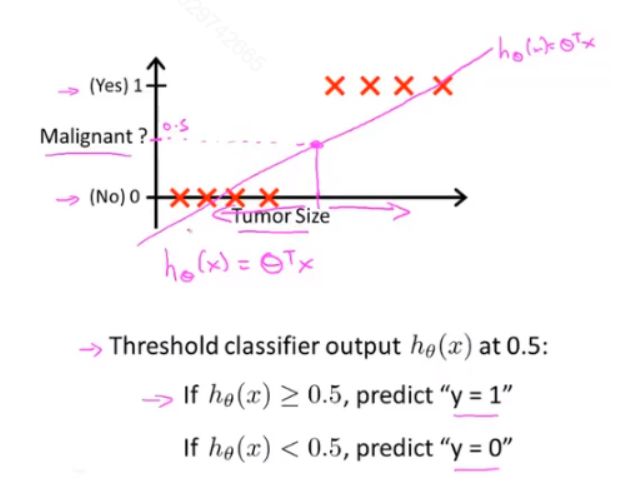
​ 下面以Tumor为例：

​ 如果用线性回归的算法的话：

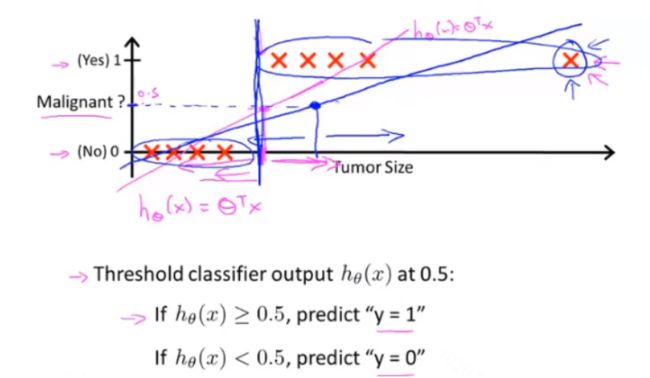
​ 似乎可行，但是如果我的数据集里多了一个这样的数据，那么拟合到的直线就会改变，阈值x也会向右移，得出的结论就不准了，得到了一个更坏的假设。

​ **所以，线性回归用到分类问题中并不是一个很好的决定。**虽然第一个例子中感觉还可以，但这只是一种巧合。

• 总结：

  如果我们要用线性回归算法来解决一个分类问题，对于分类， $y$ 取值为 0 或者1，但如果你使用的是线性回归，那么假设函数的输出值可能远大于 1，或者远小于0，即使所有训练样本的标签 $y$ 都等于 0 或 1。

  尽管我们知道标签应该取值0 或者1，但是如果算法得到的值远大于1或者远小于0的话，就会感觉很奇怪。所以我们在接下来的要研究的算法就叫做逻辑回归算法，这个算法的性质是：它的输出值永远在0到 1 之间。

  并且，不要看他的名字叫回归，实际上它是一个分类算法，取这个名是因为某些历史原因。总之，大家记住，逻辑回归是一种分类算法。

6.2 假设陈述 ——sigmoid 函数

• 我要给你展示假设函数的表达式，**也就是说，在分类问题中，要用什么样的函数来表示我们的假设。**此前我们说过，希望我们的分类器的输出值在0和1之间，因此，我们希望想出一个满足某个性质的假设函数，这个性质使它的预测值要在0和1之间。

• 回顾在一开始提到的乳腺癌分类问题，我们可以用线性回归的方法求出适合数据的一条直线：

根据线性回归模型我们只能预测连续的值，然而对于分类问题，我们需要输出0或1，我们可以预测：

当$h_{\theta }\left(x\right)>=0.5$时，预测 $y=1$。

当$h_{\theta }\left(x\right)<0.5$时，预测 $y=0$ 。

对于上图所示的数据，这样的一个线性模型似乎能很好地完成分类任务。假使我们又观测到一个非常大尺寸的恶性肿瘤，将其作为实例加入到我们的训练集中来，这将使得我们获得一条新的直线。

这时，再使用0.5作为阀值来预测肿瘤是良性还是恶性便不合适了。可以看出，线性回归模型，因为其预测的值可以超越[0,1]的范围，并不适合解决这样的问题。

• 我们引入一个新的模型，逻辑回归，该模型的输出变量范围始终在0和1之间。 -
  • 逻辑回归模型的假设是： $h_{\theta }\left(x\right)=g\left({\theta }^{T}X\right)$
  • 其中： $X$ 代表特征向量
  • $g$ 代表逻辑函数（logistic function)是一个常用的逻辑函数为S形函数（Sigmoid function），公式为： $g\left(z\right)=\frac{1}{1+e^{-z}}$。
  • sigmoid function 和 logistic function 就是一个东西，是可以互换的。
  • 该函数的图像为：

• python代码实现：

import numpy as np
    
def sigmoid(z):
    
   return 1 / (1 + np.exp(-z))

• $h_{\theta }\left(x\right)$的作用是，对于给定的输入变量，根据选择的参数计算输出变量=1的可能性（estimated probability，通过已经确定的参数计算得出$h_{\theta }\left(x\right)=0.7$，则表示有70%的几率$y$为正向类，相应地$y$为负向类的几率为1-0.7=0.3。

6.3 决策边界 Decision Boundary

• 现在讲下决策边界(decision boundary)的概念。这个概念能更好地帮助我们理解逻辑回归的假设函数在计算什么。
• 例：

• 这个例子中决策边界就是这条直线：x1 + x2 = 3

• 注意：

  • 决策边界是假设函数的一个属性，包括$\theta ,$${\theta }_1$,${\theta }_2$。
  • 即：决策边界就是 g(……) 里面的 …… = 0 的这样一条直线or曲线。
  • 它是假设函数的一个固有属性，即使没有数据集，假设函数的决策边界依旧存在。只要给定了参数 $\theta$ 的集合，决策边界就确定了【即：我们随便给一个值，都可以得到一个决策边界】。
  • 而数据集是用来拟合更好的参数 $\theta$ 的。

• 此外，我们可以用非常复杂的模型来适应非常复杂形状的判定边界，如下两个图：

6.4 代价函数

6.4.1 问题概述：

给定数据集后，我们如何选择参数 $\theta$ ？

6.4.2 尝试一：线性回归的代价函数

• 回想之前线性回归的时候，我们是用通过代价函数的值来逐渐更新参数 $\theta$ 的。这个理念同样适用。现在，我要定义用来拟合参数的优化目标（或者叫代价函数），这便是监督学习问题中的逻辑回归模型的拟合问题。

• 但如果我们直接套 线性回归的代价函数的话，得到的将是一个 $\theta$ 的非凸函数

• 有很多的局部最小值，如果将梯度下降法使用在这样一个函数上（非凸函数），不能保证他能收敛到全局最小值。

• 我们希望是一个凸函数（convex function），如右图，那么使用梯度下降法能收敛到该函数的全局最小值。

• 本质原因：对sigmoid函数用差的平方，会得到凸非函数，所以我们要找到另一个代价函数。

6.4.3 尝试二：逻辑回归的代价函数

• 分析过程：
  • 这是一个代价函数，是一种预测值和真实值之间的误差表示。
  • 先分析当 y = 1 or y = 0 时
  • 我们只选择 自变量在0~1之间。
• y=1时：
  • 若 $h_{\theta }(x)$ = 1，即我预测也为1，那么Cost = 0
  • 若 $h_{\theta }(x)$ = 0，即我预测和它正好相反，那么Cost 趋于 $ +\infty $
  • 注意这里一个是等于，一个是趋于。
  • 【反应到现实生活中，如果我们预测某个病人的肿瘤是恶性的概率为99%，但最后他还是有1%可能是良性的。我理解为：预测是一种概率，没有一定的100%】
    
• y=0时：
  

6.5 简化的代价函数和梯度下降

6.5.1 对公式的简化

• 目的：在这段视频中，我们将会找出一种稍微简单一点的方法来写代价函数，来替换我们现在用的方法。同时我们还要弄清楚如何运用梯度下降法，来拟合出逻辑回归的参数。
• 因此，听了这节课，你就应该知道如何实现一个完整的逻辑回归算法。
• 6.4中介绍的逻辑回归代价函数如下，特征是：y 永远为 0 or 1，我们的Cost function也是依据 y 值的不同而写的。下面，我们将尝试把这两个式子，合二为一，这将帮助我们更好的使用梯度下降。

• 这个式子可以合并成：$Cost\left(h_{\theta }\left(x\right),y\right)=-y\times log\left(h_{\theta }\left(x\right)\right)-(1-y)\times log\left(1-h_{\theta }\left(x\right)\right)$

• 即，逻辑回归的代价函数： $Cost\left(h_{\theta }\left(x\right),y\right)=-y\times log\left(h_{\theta }\left(x\right)\right)-(1-y)\times log\left(1-h_{\theta }\left(x\right)\right)$ $=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}\log \left(h_{\theta }\left(x^{(i)}\right)\right)+\left(1-y^{(i)}\right)\log \left(1-h_{\theta }\left(x^{(i)}\right)\right)]$

6.5.2 梯度下降法拟合参数

• 目标：我们已经化简了代价函数。下面要做的就是：为了最小化代价函数，使用梯度下降法，逐渐拟合出参数。

  梯度下降法思想通常如下：

• 细心的旁友可以发现，蓝色框框里面和我们之前线性回归所写的竟然一样！

但实际上，这里的 $h_{\theta }(x)$ 的具体公式是不一样的。

对于线性回归假设函数：

$h_{\theta }\left(x\right)={\theta }^{T}X={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n$

而现在逻辑函数假设函数：

$h_{\theta }\left(x\right)=\frac{1}{1+e^{-{\theta }^{T}X}}$

• 因此，即使更新参数的规则看起来基本相同，但由于假设的定义发生了变化，所以逻辑函数的梯度下降，跟线性回归的梯度下降实际上是两个完全不同的东西。

• 如何监控梯度下降法以确保其收敛

  在先前的视频中，当我们在谈论线性回归的梯度下降法时，我们谈到了如何监控梯度下降法以确保其收敛，我通常也把同样的方法用在逻辑回归中，来监测梯度下降，以确保它正常收敛。

  当使用梯度下降法来实现逻辑回归时，我们有这些不同的参数$\theta $，就是${\theta_{0}}$ ${\theta }_1$ ${\theta }_2$ 一直到${\theta }_n$，我们需要用这个表达式来更新这些参数。我们还可以使用 for循环来更新这些参数值，用 for i=1 to n，或者 for i=1 to n+1。当然，不用 for循环也是可以的，理想情况下，我们更提倡使用向量化的实现，可以把所有这些 $n$个参数同时更新。

• 特征缩放应用于逻辑回归

  最后还有一点，我们之前在谈线性回归时讲到的特征缩放，我们看到了特征缩放是如何提高梯度下降的收敛速度的，**这个特征缩放的方法，也适用于逻辑回归。**如果你的特征范围差距很大的话，那么应用特征缩放的方法，同样也可以让逻辑回归中，梯度下降收敛更快。

  就是这样，现在你知道如何实现逻辑回归，这是一种非常强大，甚至可能世界上使用最广泛的一种分类算法。

6.6 高级优化 —— 相对于梯度下降

6.6.1 梯度下降

在上一个视频中，我们讨论了用梯度下降的方法最小化逻辑回归中代价函数$J\left(\theta \right)$。在本次视频中，我会教你们一些高级优化算法和一些高级的优化概念，利用这些方法，我们就能够使通过梯度下降，进行逻辑回归的速度大大提高，而这也将使算法更加适合解决大型的机器学习问题，比如，我们有数目庞大的特征量。

现在我们换个角度来看什么是梯度下降，我们有个代价函数$J\left(\theta \right)$，而我们想要使其最小化，那么我们需要做的是编写代码，当输入参数 $\theta$ 时，它们会计算出两样东西：$J\left(\theta \right)$ 以及$J$ 等于 0、1直到 $n$ 时的偏导数项。

假设我们已经完成了可以实现这两件事的代码，那么梯度下降所做的就是反复执行这些更新。 另一种考虑梯度下降的思路是：我们需要写出代码来计算$J\left(\theta \right)$ 和这些偏导数，然后把这些插入到梯度下降中，然后它就可以为我们最小化这个函数。 对于梯度下降来说，我认为从技术上讲，你实际并不需要编写代码来计算代价函数$J\left(\theta \right)$。你只需要编写代码来计算导数项，但是，如果你希望代码还要能够监控这些$J\left(\theta \right)$ 的收敛性，那么我们就需要自己编写代码来计算代价函数$J(\theta )$和偏导数项$\frac{\partial }{\partial {\theta }_j}J\left(\theta \right)$。所以，在写完能够计算这两者的代码之后，我们就可以使用梯度下降。

6.6.2 三种高级算法：共轭梯度、BFGS、L-BFGS

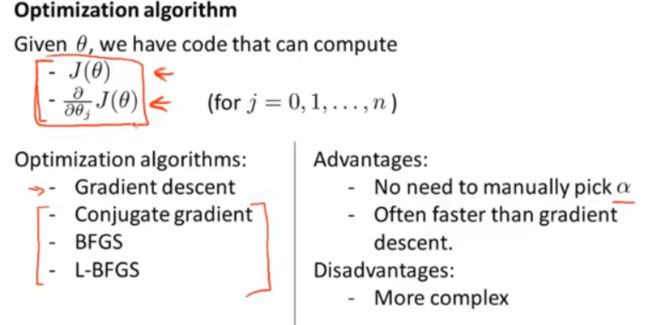
• 然而梯度下降并不是我们可以使用的唯一算法，还有其他一些算法，更高级、更复杂。如果我们能用这些方法来计算代价函数$J\left(\theta \right)$和偏导数项$\frac{\partial }{\partial {\theta }_j}J\left(\theta \right)$两个项的话，那么这些算法就是为我们优化代价函数的不同方法，共轭梯度法 BFGS (变尺度法) 和L-BFGS (限制变尺度法) 就是其中一些更高级的优化算法，它们需要有一种方法来计算 $J\left(\theta \right)$，以及需要一种方法计算导数项，然后使用比梯度下降更复杂的算法来最小化代价函数。

• 这三种算法的具体细节超出了本门课程的范畴。我们实际上完全有可能成功使用这些算法，并应用于许多不同的学习问题，而不需要真正理解这些算法的内环间在做什么。

• 这三种算法的优点：

  • 一个是使用这其中任何一个算法，你通常不需要手动选择学习率 $\alpha$，所以对于这些算法的一种思路是，给出计算导数项和代价函数的方法，你可以认为算法有一个智能的内部循环，而且，事实上，他们确实有一个智能的内部循环，称为线性搜索(line search)算法，它可以自动尝试不同的学习速率 $\alpha$，并自动选择一个好的学习速率 $a$，因此它甚至可以为每次迭代选择不同的学习速率，那么你就不需要自己选择。
  • 这些算法实际上在做更复杂的事情，不仅仅是选择一个好的学习速率，所以它们往往最终比梯度下降收敛得快多了，不过关于它们到底做什么的详细讨论，已经超过了本门课程的范围。

• 缺点：

  • 如果说这些算法有缺点的话，那么我想说主要缺点是它们比梯度下降法复杂多了。特别是你最好不要使用 L-BGFS、BFGS这些算法，除非你是数值计算方面的专家。
  • 实际上，我不会建议你们编写自己的代码来计算数据的平方根，或者计算逆矩阵，因为对于这些算法，我还是会建议你直接使用一个软件库，比如说，要求一个平方根，我们所能做的就是调用一些别人已经写好用来计算数字平方根的函数。幸运的是现在我们有Octave 和与它密切相关的 MATLAB 语言可以使用。

6.6.3 算法例子实现

• Octave 有一个非常理想的库用于实现这些先进的优化算法，所以，如果你直接调用它自带的库，你就能得到不错的结果。
• 我必须指出这些算法实现得好或不好是有区别的，因此，如果你正在你的机器学习程序中使用一种不同的语言，比如如果你正在使用C、C++、Java等等，你可能会想尝试一些不同的库，以确保你找到一个能很好实现这些算法的库。因为在L-BFGS或者等高线梯度的实现上，表现得好与不太好是有差别的，因此现在让我们来说明：如何使用这些算法：

比方说，你有一个含两个参数的问题，这两个参数是${\theta }_0$和${\theta }_1$，因此，通过这个代价函数，你可以得到${\theta }_1$和 ${\theta }_2$的值，如果你将$J\left(\theta \right)$ 最小化的话，那么它的最小值将是${\theta }_1=5$ ，${\theta }_2=5$。代价函数$J\left(\theta \right)$的导数推出来就是这两个表达式：

$\frac{\partial }{\partial \theta \ast 1}J(\theta )=2(\theta \ast 1-5)$

$\frac{\partial }{\partial \theta \ast 2}J(\theta )=2(\theta \ast 2-5)$

如果我们不知道最小值，但你想要代价函数找到这个最小值，是用比如梯度下降这些算法，但最好是用比它更高级的算法，你要做的就是运行一个像这样的Octave 函数：

function [jVal, gradient]=costFunction(theta)
    
　　jVal=(theta(1)-5)^2+(theta(2)-5)^2;
    
　　gradient=zeros(2,1);
    
　　gradient(1)=2*(theta(1)-5);
    
　　gradient(2)=2*(theta(2)-5);
    
end

这样就计算出这个代价函数，函数返回的第二个值是梯度值，梯度值应该是一个2×1的向量，梯度向量的两个元素对应这里的两个偏导数项，运行这个Cost Function 函数后，你就可以调用高级的优化函数，这个函数叫 fminunc，它表示Octave 里无约束最小化函数。调用它的方式如下：

options=optimset('GradObj','on','MaxIter',100);

initialTheta=zeros(2,1);
    
[optTheta, functionVal, exitFlag]=fminunc(@costFunction, initialTheta, options);

你要设置几个options，这个 options 变量作为一个数据结构可以存储你想要的options，所以 GradObj 和On，这里设置梯度目标参数为打开(on)，这意味着你现在确实要给这个算法提供一个梯度，然后设置最大迭代次数，比方说100，我们给出一个$\theta$ 的猜测初始值，它是一个2×1的向量，那么这个命令就调用fminunc，这个@符号表示指向我们刚刚定义的costFunction 函数的指针。如果你调用它，它就会使用众多高级优化算法中的一个，当然你也可以把它当成梯度下降，只不过它能自动选择学习速率$\alpha$，你不需要自己来做。然后它会尝试使用这些高级的优化算法，就像加强版的梯度下降法，为你找到最佳的$\theta$值。

让我告诉你它在 Octave 里什么样：

所以我写了这个关于theta的 costFunction 函数，它计算出代价函数 jval以及梯度gradient，gradient 有两个元素，是代价函数对于theta(1) 和 **theta(2)**这两个参数的偏导数。

我希望你们从这个幻灯片中学到的主要内容是：写一个函数，它能返回代价函数值、梯度值，因此要把这个应用到逻辑回归，或者甚至线性回归中，你也可以把这些优化算法用于线性回归，你需要做的就是输入合适的代码来计算这里的这些东西。

现在你已经知道如何使用这些高级的优化算法，有了这些算法，你就可以使用一个复杂的优化库，它让算法使用起来更模糊一点。因此也许稍微有点难调试，不过由于这些算法的运行速度通常远远超过梯度下降。

所以当我有一个很大的机器学习问题时，我会选择这些高级算法，而不是梯度下降。有了这些概念，你就应该能将逻辑回归和线性回归应用于更大的问题中，这就是高级优化的概念。

在下一个视频，我想要告诉你如何修改你已经知道的逻辑回归算法，然后使它在多类别分类问题中也能正常运行。

6.7 多类别分类：一对多

• 目标：在本节视频中，我们将谈到如何使用逻辑回归 (logistic regression)来解决多类别分类问题，具体来说，一个叫做"一对多" (one-vs-all) 的分类算法。

• 例如：

• 二分类和多分类图解：

• 我用3种不同的符号来代表3个类别，问题就是给出3个类型的数据集，我们如何得到一个学习算法来进行分类呢？

• 我们现在已经知道如何进行二元分类，可以使用逻辑回归，对于直线或许你也知道，可以将数据集一分为二为正类和负类。用一对多的分类思想，我们可以将其用在多类分类问题上。

• 下面将介绍如何进行"one-vs-all"的分类工作，有时这个方法也被称为"one-vs-rest"方法。

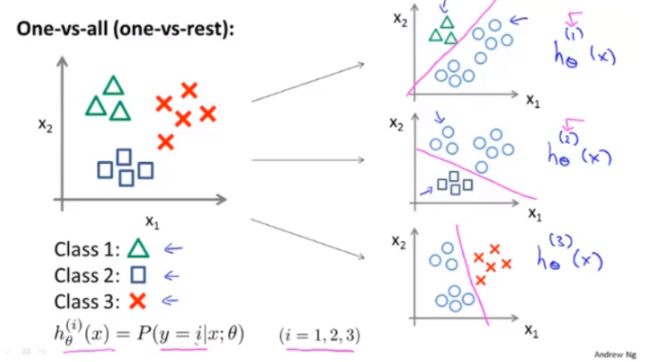
• 现在我们有一个训练集，好比上图表示的有3个类别，我们用三角形表示 $y=1$，方框表示$y=2$，叉叉表示 $y=3$。

• 我们下面要做的就是使用一个训练集，将其分成3个二元分类问题。

• 我们先从用三角形代表的类别1开始，实际上我们可以创建一个，新的"伪"训练集，类型2和类型3定为负类，类型1设定为正类，我们创建一个新的训练集，如下图所示的那样，我们要拟合出一个合适的分类器。

  这里的三角形是正样本，而圆形代表负样本。可以这样想，设置三角形的值为1，圆形的值为0，下面我们来训练一个标准的逻辑回归分类器，这样我们就得到一个正边界。

• **为了能实现这样的转变，我们将多个类中的一个类标记为正向类（$y=1$），然后将其他所有类都标记为负向类，**这个模型记作$h_{\theta }^{\left(1\right)}\left(x\right)$。接着，类似地第我们选择另一个类标记为正向类（$y=2$），再将其它类都标记为负向类，将这个模型记作 $h_{\theta }^{\left(2\right)}\left(x\right)$,依此类推。

• 训练这个逻辑回归分类器：$h_{\theta }^{\left(i\right)}\left(x\right)$， 其中 $i$ 对应每一个可能的 $y=i$

• 最后我们得到一系列的模型简记为： $h_{\theta }^{\left(i\right)}\left(x\right)=p\left(y=i|x;\theta \right)$其中：$i=\left(1,2,3....k\right)$

• 最后，在我们需要做预测时：我们将所有的分类机都运行一遍，然后对每一个输入变量，都选择最高可能性的输出变量。

  • 我们给出输入一个新的 $x$ 值，用这个做预测。我们要做的就是在我们三个分类器里面输入 $x$，然后我们选择一个让 $h_{\theta }^{\left(i\right)}\left(x\right)$ 最大的$ i$，即$\mathop{\max}\limits_i,h_\theta^{\left( i \right)}\left( x \right)$。
  • 你现在知道了基本的挑选分类器的方法，选择出哪一个分类器是可信度最高效果最好的，那么就可认为得到一个正确的分类，无论$i$值是多少，我们都有最高的概率值，我们预测$y$就是那个值。

• 这就是多类别分类问题，以及一对多的方法，通过这个小方法，你现在也可以将逻辑回归分类器用在多类分类的问题上。