YOLOV4用到的一些tricks以及代码实现（2）——CIou_Loss
本篇博客介绍用于计算损失函数的CIOU_LOSS算法
继上篇介绍yolov4——Mosaic data argumentaion后，接着介绍yolov4中用到的tricks。
CIOU_LOSS算法用于目标检测损失函数的计算。在详细介绍CIOU代码之前，有必要介绍一下CIOU的进化序列。
本节介绍交叉熵，Focal loss，L1/L2损失函数、IOU Loss、GIOU、DIOU的相关理论以及CIOU的理论与代码实线。
理论部分参考：https://zhuanlan.zhihu.com/p/104236411
交叉熵：
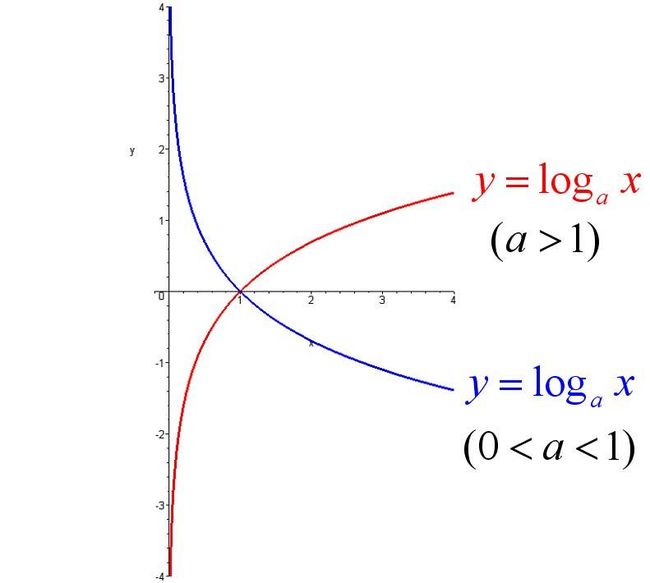
作为图像分类问题最为常用的损失函数，通常接在softmax之后，可解决大多数图像分类问题。对数函数曲线图如下所示：
通过log曲线可以发现，当y(真实值）为1时，y'（预测值)越大，loss越小。同样，当y为0时，y'越小，预测值越小。这样存在大量的迭代学习用于容易分类的对象上。
Focal loss
由此出现了Focal loss函数：
Focal loss函数在原有的交叉熵函数中增加一项，如下图所示：
Focal loss中，易于分类的对象有较小的损失值，难以分类的对象有较大的损失值。其中gamma>0。以gamma=2为例，计算当y=1时，不同y'得出的loss值。
Focal loss 交叉熵：
当y'=0.9时，loss=0.0010536051 当y'=0.9时，loss= 0.105360515
当y'=0.1时，loss=1.865093925 当y'=0.1时，loss= 2.3025850929
计算结果可见，对于y'值较大时，Loss的值会变得很小。
Focal Loss 适用于one hot之后的图像分类问题，并不适用于目标检测。因为目标检测后的box中的x,y,w,h有相关性并不是相互独立的，不能简单地当作一个回归问题来解决。因此IOU LOSS出现了。
IOU LOSS
IOU LOSS将坐标之间的相关性考虑在内，先看下经典的图片：
通过上图可以发现，通过坐标点进行回归之后的loss值相同的情况下，预测的位置坐标与真实坐标相差很大。
上图展示了L2 Loss和IoU Loss 的求法，图中红点表示目标检测网络结构中Head部分上的点（i,j），绿色的框表示GT框, 蓝色的框表示Prediction的框。算法步骤如下：
IOU就是求两个框的交并比。唯一需要注意的是，论文中使用的是-ln(IOU),而我们实际大多数会使用1-IOU。
IOU LOSS 存在的问题是，如果预测框和目标框不相交的话，IOU=0，这样损失函数不可导也就无法优化。
GIOU
如上图所示，三种不同相对位置的框拥有相同的IoU=0.33值，但是拥有不同的GIoU=0.33，0.24，-0.1。当框的对齐方向更好一些时GIoU的值会更高一些。
除此以外，IOU不能反映两个框是如何相交的。例如anchor与实际尺寸相差较大，甚至完全包括住实际框，这样实际框只要在anchor中，其IOU的值都是相同的。因此出现了DIOU
DIOU
相对于GIOU，DIOU增加了新的惩罚项，公式为：
最后一项增加了中心点间距离的惩罚性，可以很好的解决anchor和预测框之间尺度相差过大而包裹起来的问题。这样可以做到尺度无关性。
CIOU
本文着重介绍CIOU，它也是现在目标检测中效果最好的Loss计算方法。接下来从原理到代码详细解析：
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-imHjpoo6-1595681540590)(C:\Users\Administrator\Desktop\YOLOv4\20.png)]](http://img.e-com-net.com/image/info8/58b9c7d7c70941e086bff4d2264d3330.jpg)
其中，
代表了预测框和真实框的中心点的欧式距离。 c代表的是能够同时包含预测框和真实框的最小闭包区域的对角线距离。
LOSS公式为
分析CIOU LOSS的公式，发现比普通的IOU增加了两个惩罚项。bbox回归应该考虑到三个要素：覆盖面积，中心点距离和长宽比。
对比上述公式，发现完美的解决的这三个问题。CIOU也是由IOU->GIOU->DIOU->CIOU一步步进化成型。每一次进化都是围绕着上诉三要素进行的。
GIOU:为了归一化坐标尺度，利用IOU，并初步解决了IOU为零的情况。
DIOU：DIOU损失考虑边界框重叠和中心距离的问题。
CIOU：在DIOU的基础上加入长宽比惩罚项。
难怪作者将其起名为Complete-IOU Loss。完整的IOU损失。
CIOU在yoloV4中的代码实现与分析：
yolov4源码中的CIOU实现如下：
b1_xy = b1[1:3]
b1_wh = b1[3:5]
b1_wh_half = b1_wh / 2.
b1_mins = b1_xy - b1_wh_half
b1_maxes = b1_xy + b1_wh_half
b2_xy = b2[1:3]
b2_wh = b2[3:5]
b2_wh_half = b2_wh / 2.
b2_mins = b2_xy - b2_wh_half
b2_maxes = b2_xy + b2_wh_half
注：上述代码与源码中略有不同，源码因为包裹在train中计算，因此维度有所不同。本博客传入y_true和y_pre传入的b1和b2维度相同，分别表示[batch,mid_x,mid_y,w,h]。
上述代码计数出y_true和y_pre左上角坐标和右下角坐标。
intersect_mins = K.maximum(b1_mins, b2_mins)
intersect_maxes = K.minimum(b1_maxes, b2_maxes)
intersect_wh = K.maximum(intersect_maxes - intersect_mins, 0.)
intersect_area = intersect_wh[..., 0] * intersect_wh[..., 1]
b1_area = b1_wh[..., 0] * b1_wh[..., 1]
b2_area = b2_wh[..., 0] * b2_wh[..., 1]
union_area = b1_area + b2_area - intersect_area
iou = intersect_area / K.maximum(union_area, K.epsilon())上述代码用于计算IOU。其中有个细节是：K.epsilon()用法:这里返回一个1e-0.7。这里是为了防止梯度爆炸。
# 计算中心的差距
center_distance = K.sum(K.square(b1_xy - b2_xy), axis=-1)
# 找到包裹两个框的最小框的左上角和右下角
enclose_mins = K.minimum(b1_mins, b2_mins)
enclose_maxes = K.maximum(b1_maxes, b2_maxes)
enclose_wh = K.maximum(enclose_maxes - enclose_mins, 0.0)
# 计算对角线距离
enclose_diagonal = K.sum(K.square(enclose_wh), axis=-1)
ciou = iou - 1.0 * (center_distance) / K.maximum(enclose_diagonal, K.epsilon())
计算包裹框大小是为了实现GIOU的核心思想。
计算对角线距离是为了实现DIOU的核心思想。
v = 4*K.square(tf.math.atan2(b1_wh[..., 0], K.maximum(b1_wh[..., 1],K.epsilon())) - tf.math.atan2(b2_wh[..., 0], K.maximum(b2_wh[..., 1],K.epsilon()))) / (math.pi * math.pi)
alpha = v / K.maximum((1.0 - iou + v), K.epsilon())
ciou = ciou - alpha * v
ciou = K.expand_dims(ciou, -1)
ciou = tf.where(tf.math.is_nan(ciou), tf.zeros_like(ciou), ciou)最后计算alpha和v的值，加入长宽信息。上述代码均实现数学公式，没有特别指出。唯一值得注意的是：tf.where（）用法，这里也是为了代码鲁棒性考虑
where(condition, x=None, y=None,name=None)
condition:一个Tensor,数据类型为tf.bool类型
如果x、y均为空，那么返回condition中值为True的位置的Tensor：例如：x就是condition，y是返回值。