python 实现对偶单纯形法

昨天熬了一个通宵，女朋友写运筹学作业有个对偶单纯形法的题，据说是算了一天，感觉题无解，但是想确定一下，就很烦躁。我开始搜了一下，但是网上的代码都用不了，所以咱就研究了一下单纯形法和对偶单纯形法，用python写了个程序，百分百可用！用不了私信我！

对偶单纯形法

对偶单纯形法是指从对偶可行性逐步搜索出原始问题最优解的方法。由线性规划问题的对偶理论，原始问题的检验数对应于对偶问题的一组基本可行解或最优解；原始问题的一组基本可行解或最优解对应于对偶问题的检验数；原始问题约束方程的系数矩阵的转置是对偶问题约束条件方程的系数矩阵。所以，在求解常数项小于零的线性规划问题时，可以把原始问题的常数项视为对偶问题的检验数，原始问题的检验数视为对偶问题的常数项。

原理就不说了，直接上代码

from fractions import Fraction
# print(Fraction(2,2))
Cj=[-15,Fraction(3,4),-5,0,0] #要求的函数
list1=[[-2,0,-6,-1,1,0],[-1,-5,-2,-1,0,1]] #每个子列表第一位为b
z=[0,-15,-24,-5,0,0]#
Xb=[4,5]#
Cb=[0,0]
def show():

    print("--" * 50)
    print("|               Cj               ",end='|')
    for i in Cj:
        print(str(i).center(10),end='|')
    print(" "*10+"|")
    print("--"*50)
    print("|    Cb    |    Xb    |    b     ",end='|')
    for i in range(len(Cj)):
        print(("X"+str(i+1)).center(10),end='|')
    print(" "*10+"|")
    print("--" * 50)
    for i in range(len(list1)):
        print("|",end="")
        print(str(Cb[i]).center(10),end='|')
        print(("X"+str(Xb[i])).center(10),end='|')
        print(str(list1[i][0]).center(10),end="|")
        for j in range(1,len(list1[1])):
            print(str(list1[i][j]).center(10),end="|")
        print(" " * 10 + "|")
        print("--" * 50)
    print("|          Z          ",end='|')
    for i in range(len(z)):
        if i==0:
            print(str(z[i]).center(10),end='|')
        else:
            print(str(z[i]).center(10), end='|')
    print(" "*10+"|")
    print("--" * 50)
    print("**" * 50)
def fu():
    min_=0
    for i in range(len(list1)):
        if list1[i][0] 0:
            flag = 0
            break
    if flag==0:
        fu()
        show()
    else:
        break

11/15修复了输出函数

要修改的部分

Cj=[-9,-12,-15,0,0,0] #要求的函数
list1=[[-10,-2,-2,-1,1,0,0],[-12,-2,-3,-1,0,1,0],[-14,-1,-1,-5,0,0,1]] #每个子列表第一位为b
z=[0,-9,-12,-15,0,0,0]#
Xb=[4,5,6]#
Cb=[0,0,0]#

在程序里这几个列表都是通过相同下标相关，看图和上面对应应该可以看懂，不会用直接私信我或者评论都可以！

注：分数要用Fraction(分子,分母)这么写，如：

 

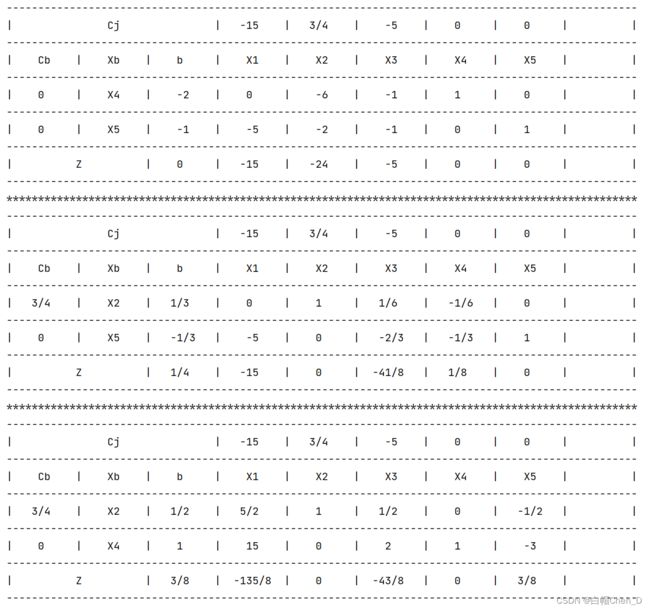
例题运行结果