【目标检测】雷达目标CFAR检测算法
目录
- 一、概述
-
- 1、基本概念
- 2、基础知识
- 二、CFAR检测算法
-
- 1、基本原理
- 2、几种典型的CFAR检测算法
-
- (1)CA(Cell Averaging)-CFAR检测算法
- (2)GO-CFAR、SO-CFAR检测算法
- (3)OS-CFAR检测算法
- (4) 补充说明
- 三、不同CFAR检测算法性能对比
-
- 1、MATLAB仿真结果
- 2、MATLAB代码
- 3、优缺点总结
- 四、参考文献
一、概述
1、基本概念
雷达的检测过程可用门限检测来描述。几乎所有的判断都是以接收机的输出与某个门限电平的比较为基础的,如果接收机输出的包络超过了某一设置门限,就认为出现了目标。
雷达在探测时会受到噪声、杂波和干扰的影响,因而采用固定门限进行目标检测时会产生一定的虚警,特别是当杂波背景起伏变化时虚警率会急剧上升,严重影响雷达的检测性能。因此,根据雷达杂波数据动态调整检测门限,在虚警概率保持不变的情况下实现目标检测概率最大化,这种方法称为恒虚警率(Constant False Alarm Rate,CFAR)检测技术。
2、基础知识
雷达在判决过程中,可能会出现两类错误。第一类是在没有目标时判断为有目标,这类错误称为虚警。另一类是在有目标时判断为没有目标,这类错误称为漏警。以上两类错误以一定的概率出现,分别称为虚警概率和漏警概率。
二、CFAR检测算法
目前,研究人员针对各种杂波环境下提出了许多高效的CFAR检测算法,大体可分为两类:一类是均值类CFAR(CA-CFAR)算法,该类算法应用的前提是假设背景杂波是均匀分布的;另一类是有序统计类CFAR(OS-CFAR)算法,这类算法是为了应对邻域内多目标情况而设计的。不同CFAR检测算法各有优劣,都是针对具体情况而设计,我们只需要学习CFAR的基本原理以及熟悉几种典型的CFAR检测算法即可。
1、基本原理
CFAR检测器的输入一般包括检测单元 Y Y Y 和 2 n 2n 2n 个参考单元。参考单元位于检测单元两侧,前后各 n n n 个。保护单元主要用在单目标情况下,防止目标能量泄漏到参考单元影响检测效果。设参考门限电平为 V T H V_{TH} VTH, V T H = T × Z V_{TH}=T×Z VTH=T×Z,其中: Z Z Z 为总的杂波功率水平的估计, T T T 为门限因子,则当 Y > V T H Y>V_{TH} Y>VTH 时,认为有目标;反之,认为没有目标。
CFAR算法的处理流程如下图所示:
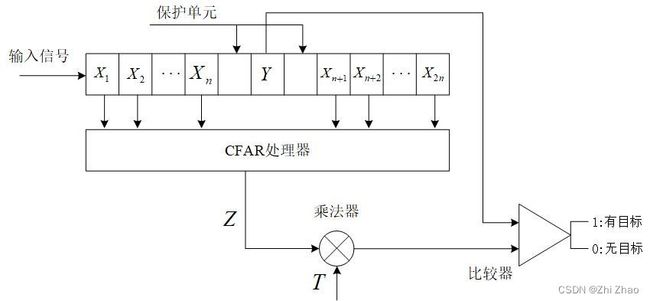
一般情况下,杂波同噪声相互独立,且平方律检波后都满足指数分布。参考单元的概率密度函数为:
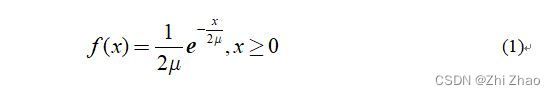
设 H 0 H_{0} H0 表示为没有目标, P [ Y > T Z ∣ H 0 ] P[Y>TZ|H_{0}] P[Y>TZ∣H0] 则表示为在没有目标的条件下判断为有目标的概率,从而得到虚警概率的表达式为:
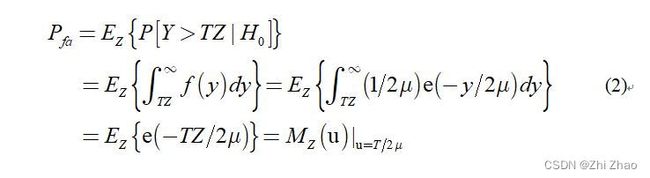
式中, μ μ μ 是噪声功率; Z Z Z 为随机变量,它的分布取决于CFAR算法的类型以及参考单元的分布; M Z ( u ) u = T / 2 μ M_{Z}(u)_{u=T/2μ} MZ(u)u=T/2μ 为矩母函数。
2、几种典型的CFAR检测算法
不同类型CFAR算法的差异主要体现为对参考单元处理的不同,亦为 Z Z Z 值选取的不同。在背景噪声独立同分布时,通过确定常数 T T T 来达到恒定的虚警概率。不同的检测算法,其确定常数 T T T 的方法也会相应的有所区别。下面将对几种典型CFAR算法的虚警概率表达式进行推导。
(1)CA(Cell Averaging)-CFAR检测算法
背景杂波功率水平 Z Z Z 的计算方式为 2 n 2n 2n个参考单元之和:
Z = ∑ i = 1 n X i + ∑ i = n + 1 2 n X i = ∑ i = 1 2 n X i Z=\sum_{i=1}^{n}X_{i}+\sum_{i=n+1}^{2n}X_{i}=\sum_{i=1}^{2n}X_{i} Z=i=1∑nXi+i=n+1∑2nXi=i=1∑2nXi
在推导 P f a P_{fa} Pfa 与 T T T 的关系之前,我们先给出伽马(Γ)分布的相关知识。
Γ Γ Γ 分布的概率密度函数为:
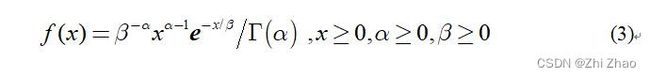
其中, α , β α,β α,β 是两个参数,当 α = 1 , β = 2 μ α=1,β=2μ α=1,β=2μ时,式(3)就退化成为式(1)中的指数分布; Γ ( α ) Γ(α) Γ(α)就是数学中的伽马函数,对于正整数 α α α,有 Γ ( α ) = ( α − 1 ) ! Γ(α)=(α-1)! Γ(α)=(α−1)!。
设 G ( α , β ) G(α,β) G(α,β) 为 Γ Γ Γ 分布的概率分布函数,若 X X X 为服从 Γ Γ Γ 分布的随机变量,则有 :

X X X 的矩母函数为:
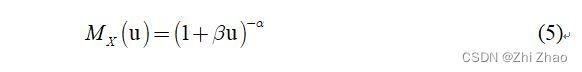
假设输入信号中的各变量满足独立同分布的条件,则对于 2 n 2n 2n个随机变量之和的矩母函数等于各随机变量的矩母函数之积,所以有:

将式(5)和式(6)以及 u = T / 2 μ u=T/2μ u=T/2μ 代入式(2),可得:
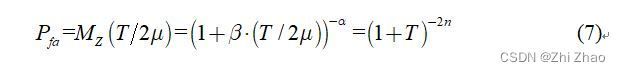
即可得到虚警概率 P f a P_{fa} Pfa 与门限因子 T T T 的关系:
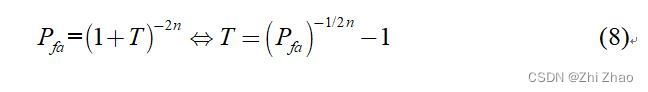
(2)GO-CFAR、SO-CFAR检测算法
最大选择GO(Greatest Of)-CFAR是选取前面 n n n 个参考单元之和与后面 n n n 个参考单元之和中的大者作为背景杂波功率水平 Z Z Z ;而最小选择SO(Smallest Of)-CFAR是选取前面 n n n 个参考单元之和与后面 n n n 个参考单元之和中的小者作为背景杂波功率水平 Z Z Z。
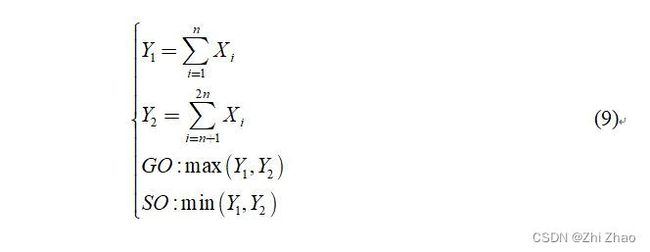
对于GO-CFAR算法,Z的概率密度函数为 f Z ( z ) f_{Z}(z) fZ(z),进而推导其虚警概率为 P f a , g o P_{fa,go} Pfa,go,如下式:
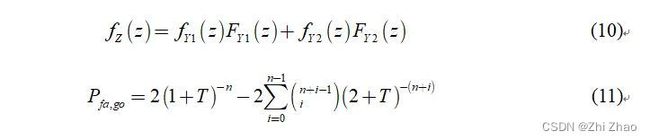
同理,可得到SO-CFAR算法的概率密度函数为 f Z ( z ) f_{Z}(z) fZ(z),虚警概率为 P f a , s o P_{fa,so} Pfa,so,如下式:
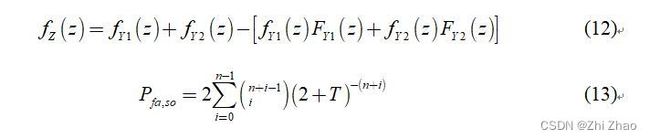
(3)OS-CFAR检测算法
顺序统计量OS(Order Statistic)CFAR的原理是先对参考单元从小到大排序,再选取第 k k k 个样本作为 Z Z Z。
设 OS-CFAR 算法的虚警概率为 P f a , o s P_{fa,os} Pfa,os,根据参考文献中的公式推导可得:
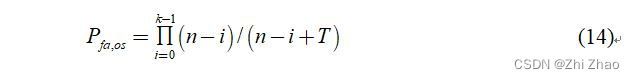
k k k 为OS-CFAR中的参数,其值的选取对算法的检测性能有较大影响。
(4) 补充说明
GO、SO、OS三类CFAR检测算法的门限因子 T T T 难以用数学表达式表示,可以通过迭代运算的方式求解出来。
当求解出门限因子 T T T 后,便可以将其代入检测概率的表达式,得到在不同信噪比的条件下,检测概率的变化情况。
在参考文献[4]和[5]中给出了检测概率 P d P_{d} Pd 的计算方法。
三、不同CFAR检测算法性能对比
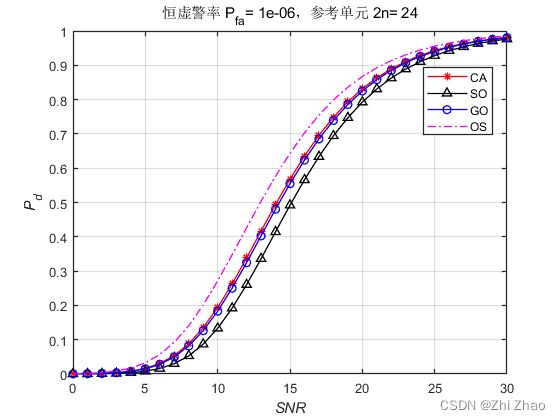
1、MATLAB仿真结果
为了比较不同CFAR算法的检测性能,建立CA、GO、SO、OS四类CFAR算法的检测概率与信噪比的关系曲线,信噪比设置为0~30dB,参考单元的数目 2 n 2n 2n 分别取16、24、32、48、64、128,保护单元左右各3个,虚警概率 P f a = 1 0 − 6 P_{fa}=10^{-6} Pfa=10−6。
MATLAB仿真结果如下图所示。
2、MATLAB代码
% ------ 程序功能:四类CFAR检测算法的检测概率与SNR的关系 %
clc
clear all;
close all;
%% 参数设置
R = 24; % 参考单元长度
n = R/2; % 半滑窗长度
k = R*3/4; % os-cfar的参数
P_fa = 1e-6; % 虚警概率
SNR_dB = (0:30); % 信噪比
SNR = 10.^(SNR_dB./10); % 信号功率与噪声功率的比值
syms T; % 门限因子的符号变量
%% CA-CFAR
T_CA = P_fa^(-1/R)-1; % CA-CFAR的门限因子
Pd_CA = (1+T_CA./(1+SNR)).^(-R); % CA-CFAR的检测概率
%% SO-CFAR、GO-CFAR
Pfa_SO = 0;
syms T
for i = 0:n-1
Pfa_SO = Pfa_SO+2*nchoosek(n+i-1,i)*(2+T)^(-(n+i)); % SO-CFAR的虚警概率表达式
end
T1_SO = solve(Pfa_SO == P_fa, T); % 求解出虚警概率为P_fa时对应的门限因子T
T2_SO = double(T1_SO);
T_SO = T2_SO(T2_SO == abs(T2_SO)); % SO-CFAR的门限因子
Pfa_GO = 2*(1+T)^(-n)-Pfa_SO; % GO-CFAR的虚警概率表达式
T1_GO = solve(Pfa_GO == P_fa, T); % 求解出虚警概率为P_fa时对应的门限因子T
T2_GO = double(T1_GO);
T_GO = T2_GO(T2_GO == abs(T2_GO)); % GO-CFAR的门限因子
Pd_SO = 0;
Pd_GO = 0;
for j = 0:n-1
Pd_SO = Pd_SO+2*nchoosek(n+j-1,j).*(2+T_SO./(1+SNR)).^(-(n+j)); % SO-CFAR的检测概率
Pd_GO = Pd_GO+2*nchoosek(n+j-1,j).*(2+T_GO./(1+SNR)).^(-(n+j));
end
Pd_GO = 2.*(1+T_GO./(1+SNR)).^(-n)-Pd_GO; % GO-CFAR的检测概率
%% OS-CFAR
Pfa_OS = k*nchoosek(R,k)*gamma(R-k+1-T)*gamma(k)/gamma(R+T+1); % OS-CFAR的虚警概率表达式
T1_OS = solve(Pfa_OS == P_fa, T); % 求解出虚警概率为P_fa时对应的门限因子T
T2_OS = double(T1_OS);
T_OS = T2_OS(T2_OS == abs(T2_OS)); % OS-CFAR的门限因子
Pd_OS = k*nchoosek(R,k)*gamma(R-k+1-T_OS./(1+SNR))*gamma(k)./gamma(R+T_OS./(1+SNR)+1); % OS-CFAR的检测概率
%% 画图
figure;
plot(SNR_dB,Pd_CA,'r-*');
hold on;
plot(SNR_dB,Pd_SO,'k-^');
plot(SNR_dB,Pd_GO,'b-o');
plot(SNR_dB,Pd_OS,'m-.');
grid on;
xlabel('SNR','FontName','Time New Romans','FontAngle','italic');
ylabel('P_{d}','FontName','Time New Romans','FontAngle','italic');
title(['恒虚警率 P_{fa}= ',num2str(P_fa),',参考单元 2n= ',num2str(R)]);
legend('CA','SO','GO','OS');
3、优缺点总结

在实际应用中,由于雷达的硬件运算资源有限,较普遍采用的算法依然复杂度较低的CA-CFAR检测算法。
四、参考文献
[1] 邹成晓, 张海霞, 程玉堃. 雷达恒虚警率检测算法综述[J]. 雷达与对抗, 2021, 41(02): 29-35.
[2] 刘朝军, 张欣, 王守权. 雷达目标恒虚警检测算法研究[J]. 舰船电子工程, 2008(07): 107-109.
[3] 崔宁, 罗运华, 喻忠军, 等. 一种基于改进卷积核的快速二维CFAR算法[J]. 现代雷达, 2020, 42(08): 30-35.
[4] 王蓓. 基于杂波图的恒虚警处理技术研究[D]. 西安电子科技大学, 2018.
[5] Detection loss due to interfering targets in ordered statistics CFAR.