【2】谷歌2021模型量化白皮书《A White Paper on Neural Network Quantization》
2021 google模型量化白皮书
- 导读
- 离线量化(PTQ)
-
- 量化范围设置
-
- Min-max方法
- Mean squared error(MSE)
- Cross entropy
- BN based range setting
- 方法比较
- Cross-Layer Equalization(CLE)
- Absorbing high biases
- Bias correction
-
- 经验偏差校正
- 分析偏差校正
- AdaRound
导读
上篇博客我们介绍了模型量化的硬件背景和基础知识,也了解到模型量化主要分为两类:离线量化(PTQ)和感知量化(QAT)。这一节主要跟大家一起了解离线量化。
离线量化(PTQ)
PTQ算法的工作原理:给定一个训练好的精度FP32的网络,在不使用训练pipeline的前提下直接将其转换为一个定点精度网络。 离线量化不需要额外的数据或只需要一个小的校准集(通常很容易获得)。因为无需使用pipeline,离线量化基本不需要超参数微调,这使得工程人员可以通过一个叫做 "black-box"方法的API去量化训练好的模型。
PTQ中比较基础且重要的步骤是为每一个量化器寻找最好的量化范围。接下来使用多种常见的方法寻找好的量化参数,然后发现PTQ过程中容易出现的问题并给出解决问题的技术方法。
量化范围设置
在网络量化过程中,变量 x x x 通过量化和重新量化两步得到与之接近的 x ^ \hat{x} x^ :
x ^ = q ( x ; s , z , b ) = s [ c l a m p ( ⌊ x s ⌉ + z ; 0 , 2 b − 1 ) − z ] \hat{x}=q(x;s,z,b)=s[clamp(\left \lfloor {\frac{x}{s}} \right \rceil + z; 0, 2^b-1)-z] x^=q(x;s,z,b)=s[clamp(⌊sx⌉+z;0,2b−1)−z]
其中 ⌊ . ⌉ \left \lfloor . \right \rceil ⌊.⌉表示四舍五入,
而clamp操作符的定义为:
c l a m p ( x ; a , c ) = { a , if x < a , x , if a < x < c , c , if x > c . clamp(x;a,c)=\begin{cases} a, & \text{ if } x
通过上边的式子,我们可以通过 ⌊ . ⌉ \left \lfloor . \right \rceil ⌊.⌉和 c l a m p clamp clamp两种操作符确定变量的范围[ q m i n , q m a x q_{min}, ~q_{max} qmin, qmax],其中 q m i n = − s z , q m a x = s ( 2 b − 1 − z ) q_{min}=-sz, ~q_{max}=s(2^b-1-z) qmin=−sz, qmax=s(2b−1−z)。但同时这两种操作符也会带来其相应的误差:rounding error 和 clipping error。
如果我们要降低 clipping error, 我们可以通过增大 s 来扩大量化范围,让更多的变量能够落进量化范围从而避免被裁减。然而增大 s (s是浮点类型转为定点类型的比例系数)会导致 rounding error 提升,因为 rounding error 的范围在[ − 1 2 s , 1 2 s -\frac{1}{2}s,~\frac{1}{2}s −21s, 21s]。所以仔细地选取量化范围能够帮助我们在 clipping error 和 rounding error 之间做trade-off。
量化范围设置指的是确定阈值 q m i n q_{min} qmin 以及 q m a x ~q_{max} qmax,关键在于如何在 clipping error 和 rounding error 之间做trade-off。下面介绍的每种方法都在两个误差之间提供了不同的权衡。这些方法通常优化局部损失函数而不是任务总损失。 这是因为在 PTQ 中,我们的目标是计算快速的方法,而不需要端到端的训练。
通常,权重可以在不需要校准数据的情况下进行量化。然而,确定激活量化的参数通常需要几批校准数据。
Min-max方法
Min-max方法将表示量化范围的参数表示如下:
V V V是即将被量化的张量,这表明[ q m i n , q m a x q_{min},~q_{max} qmin, qmax]覆盖了张量所表达的整个范围。意味着不会产生 clipping error ,但是这样会带来新的问题:对于离群点或者噪声很敏感,离群点会扩大量化范围增加 rounding error 。
Mean squared error(MSE)
基于MSE的量化范围设置方法可以解决离群点带来的问题,这种方法主要通过最小化原始张量和量化后的张量之间的MSE误差来确定量化范围。
V ^ ( q m i n , q m a x ) \hat{V}(q_{min},q_{max}) V^(qmin,qmax)表示 V V V经过量化后的张量, ∥ . ∥ \left\| . \right\| ∥.∥表示弗罗贝尼乌斯范数。
该问题的优化通常采用网格搜索、黄金分割法或具有封闭形式解的解析近似。除此之外,还存在这种范围设置方法的几种变体,但它们在目标函数和优化方面都非常相似。
Cross entropy
对于某些特定的层,被量化的张量中的所有元素可能并不同等重要。比如分类网络中的逻辑回归(logits)层,在其被量化后,保持元素内的顺序对最后的分类结果很关键。在这种场景下,MSE便不是一种合适的评价标准,因为它平等对待张量内所有的元素,从而没有考虑它们之间的次序问题。对于大量的类,我们通常有大量对预测准确性不重要的小或负 logit,而重要的较大值很少。 在这种情况下,MSE 将对少数较大的重要 logit 产生较大的量化误差,同时试图减少更多的较小 logit 的量化误差。在这种情况下,使用cross entropy作为损失函数是比较好的。
其中, H ( . , . ) H(.~,.) H(. ,.)表示cross entropy函数, ψ ( . ) \psi(.) ψ(.)指的是softmax函数,v是logits向量(经过sigmoid函数输出的向量)。
BN based range setting
对于激活值相关量化器的范围设定,通常需要一些标定数据。如果一个网络层有BN激活,激活值的每通道均值和标准差分别等于学习的BN的偏移 α \alpha α 和尺度参数 β \beta β ,然后可以使用这些来为激活值的量化器找到合适的参数,如下所示:
其中, α \alpha α和 β \beta β是每通道学习移位和比例参数的向量,并且 α \alpha α>0。
方法比较
在表 1 中,比较了权重量化的范围设置方法。 对于高位宽,MSE 和 min-max 方法大多是相当的。 然而,在较低的位宽下,MSE 方法明显优于 min-max。
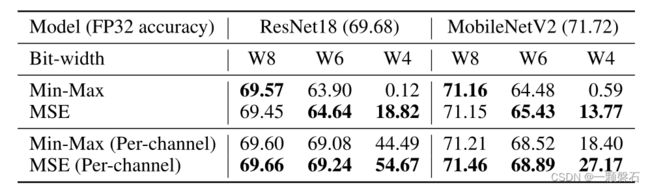
表1. 比较不同权重量化的范围设置方法
在表 2 中,对激活值量化进行了类似的比较。 我们注意到 MSE 与最后一层的交叉熵相结合,表示为 MSE + Xent,优于其他方法,尤其是在较低位宽时。 该表还清楚地展示了在最后一层使用交叉熵而不是 MSE 目标的好处。

表2. 比较不同激活值量化的范围设置方法
Cross-Layer Equalization(CLE)
量化误差的一个常见问题是同一张量中的元素的幅度可能显著不同。 如上一节所述,量化范围设置试图在rounding error 和 clipping error 之间找到一个很好的折中。 不幸的是,在某些情况下,它们之间的幅度差异如此之大,以至于即使对于中等量化(例如,INT8),我们也无法找到合适的折中方案。
有研究表明,由于只有少量权重与输出的每层特征图有关,这种现象在深度可分离卷积层中更普遍,而且这可能导致权重之间的差异性更大。此外,研究指出,BN Folding 加剧了这种效果,并可能导致连接到各种输出通道的权重之间的严重不平衡,详情见图1。虽然后者对于更细粒度的量化方式(例如,per-channel quantization)来说不是问题,但是对于应用更为广泛的 per-tensor quantization来说是个大问题。一些文献指出对于包含深度可分离卷积层的高效模型(比如MobilNet v1 和 MobileNetV2),PTQ表现出了明显的性能下降,,甚至出现了性能随机的现象。
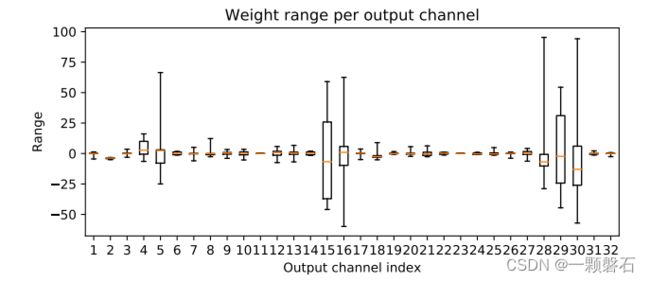
图1. BN folding后 MobileNetV2 中第一个深度可分离层的每个输出通道的权重范围。箱线图显示了每个通道的最小值和最大值、第二和第三四分位数以及中位数。
有人提出了一种无需使用per-channel quantization即可克服这种不平衡的解决方案。他们发现,许多常见的激活函数(比如ReLU、PreLu)对于任何非负实数 s s s 呈现出 positive scaling equivariance 的性质:
这种性质适用于任何一阶齐次函数,并且可以通过缩放其参数化(例如 ReLU6)扩展为也适用于任何分段线性函数。我们可以在神经网络的连续层中利用这种 positive scaling equivariance。给定两个网络层 h = f ( w ( 1 ) x + b ( 1 ) ) h = f(w^{(1)}x+b^{(1)}) h=f(w(1)x+b(1)) 和 y = f ( w ( 2 ) x + b ( 2 ) ) y=f(w^{(2)}x+b^{(2)}) y=f(w(2)x+b(2)),通过scaling equivariance得到
S = d i a g ( s ) S=diag(s) S=diag(s)是对角矩阵,对角元素 s i i s_{ii} sii 保存的是神经元 i i i 的缩放系数 s i s_i si。公式中我们相当于对原先的权重和偏置做了重参数化,其中
在 CNN 中,缩放将按通道进行,并在空间维度上相应地广播。在图 2 中说明了这个重新缩放过程。
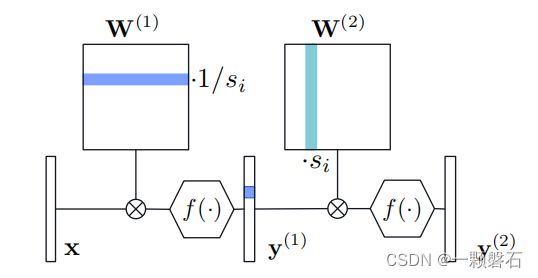
图2. 单个通道的重新缩放图示。 通过缩放系数 s i s_i si 缩放第一层中的一个通道会导致第二层中的等效通道使用 1 / s i 1/ s_i 1/si 重新参数化。
为了使得模型对量化更加鲁棒,我们可以找到一个缩放系数 s i s_i si
使得重新缩放层的量化噪声最小。cross-layer equalization 过程通过均衡连续层的动态范围来实现这一点。该方法证明了可以通过以下公式设置 S 来实现最优的权重均衡
Absorbing high biases
Nagel等人的研究工作指出,即便添加了CLE,在一些情况下过高的偏置bias也能导致激活值动态范围的差异。因此,他们提出了一种方法:如果可以,将较大的偏执bias添加到下一层。过程用公式描述如下:
其中,
h ~ = h − c \tilde{h}=h-c h~=h−c
b ~ ( 1 ) = b ( 1 ) − c \tilde{b}^{(1)}=b^{(1)}-c b~(1)=b(1)−c
函数f为ReLU激活。对于非负向量c来说,有
对于普通解c=0,适用于任何x。然而,根据 x 的分布以及 W 和 b 的值,可能存在一些 c i > 0 c_i > 0 ci>0的值,对于经验分布中的(几乎)所有 x,这种等式成立。
Bias correction
另一个常见问题是量化误差通常是有偏差的。 这意味着原始和量化层或网络的预期输出发生了偏移( E [ w x ] ! = E [ w ^ x ] E[wx]~!=E[\hat{w}x ] E[wx] !=E[w^x])。这种误差在深度可分离层(每个输出的通道只有很少的参数,通常3×3的卷积核有9个参数)中更为明显。这种误差通常由 clipping error 产生,因为一些过度裁剪的异常值可能会导致预期分布的变化。
一些论文也指出了这个问题,并且提出了一些方法来解决。对于一个层量化后的权重 w ^ \hat{w} w^,它存在着量化误差 Δ w = w ^ − w \Delta w=\hat{w}-w Δw=w^−w,我们期望输出的分布为
请注意,此校正项是与偏差具有相同形状的向量,因此可以在推理时被吸收到偏差中而无需任何额外开销。 有几种计算偏差校正项的方法,其中最常见的两种是经验偏差校正和分析偏差校正。
经验偏差校正
如果我们可以访问校准数据集,则可以通过比较量化和全精度模型的激活值来简单地计算偏差校正项。 在实际中,这可以按照以下公式逐层计算:
分析偏差校正
Nagel在2019年提出了一种方法,在不需要数据的前提下分析地计算偏置误差。对于常见的包含BN层和ReLU激活层的网络来说,他们使用前一层的 BN 统计数据来计算预期的输入分布 E [ x ] E[x] E[x] ,BN层的参数 γ \gamma γ和 β \beta β对应于BN层输出的均值和方差。我们假设输出值是符合正态分布的,ReLU 对分布的影响可以使用裁剪的正态分布来建模。公式表示如下:
其中, x p r e x^{pre} xpre是ReLU激活前的值,可以假设它符合正态分布(各通道均值为 β \beta β,方差为 γ \gamma γ), ϕ ( . ) \phi (.) ϕ(.)为标准正态分布的累积分布指数, N ( . ) N(.) N(.)用来表示标准正态分布的概率密度函数。注意,所有的向量操作都是元素级(per-channel)操作的。计算出输入的分布 E [ x ] E[x] E[x]之后,校正项就可以通过 E [ x ] E[x] E[x]乘以量化误差 Δ w \Delta w Δw得到。
AdaRound
神经网络的权重通过使用 ⌊ . ⌉ {\left \lfloor . \right \rceil } ⌊.⌉操作将每个FP32的浮点类型权重投影到最近的量化网格点。我们称这种量化操作为 rounding-to-nearest。使用 rounding-to-nearest 策略的动机为:对于一个固定的量化网格,它在浮点和量化权重之间产生最低的 MSE。然而,Nagel等人认为在PTQ中, rounding-to-nearest 不是最优解。为了说明这一点,Nagel使用 100 个不同的随机舍入样本将 ResNet18 第一层的权重量化为 4 位,并评估了每个舍入选择的网络性能。实验结果显示,最好的舍入选择方法要比 rounding-to-nearest 高出10%。图 3 通过在 y 轴上绘制这些舍入选择的性能来说明这一点。 在本节中,我们将描述 AdaRound(Nagel 等人,2020 年),这是一种为 PTQ 寻找良好权重舍入选择的系统方法。 AdaRound 是一种理论上有充分根据且计算效率高的方法,在实践中显示出显着的性能改进。
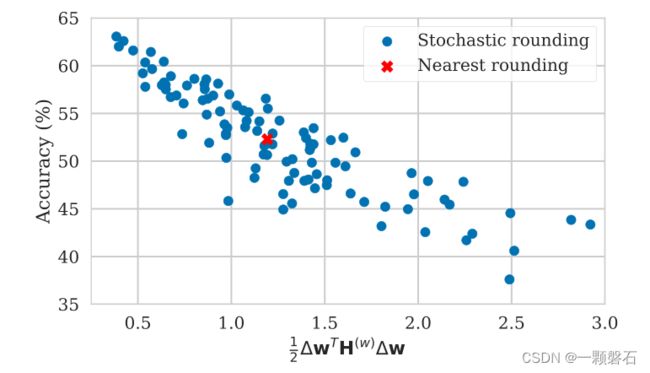
图3. 仅对 ResNet18 的第一层进行 4 位量化, 100 个随机舍入向量 w ^ \hat{w} w^ 的 ImageNet 验证准确度 (%) 之间的相关性。
由于主要目标就是要最小化量化对任务损失大小的影响,数学表达为:
其中 Δw 表示由于量化引起的扰动,并且可以为每个权重取两个可能的值,一个通过将权重向上舍入,另一个通过将权重向下舍入。 我们想有效地解决这个二元优化问题。 作为第一步,我们使用二阶泰勒级数展开来近似损失函数。 这减轻了在优化期间对每个新舍入选择进行性能评估的需要。 我们进一步假设模型已经收敛,这意味着可以忽略梯度项在近似中的贡献,并且 Hessian 是块对角线,忽略了跨层相关性。这导致以下基于 Hessian 的二次无约束二元优化 (QUBO) 问题:
图 3 中等式 (30) 的验证准确度和目标之间的明显相关性表明后者可以很好地代表任务损失,即使对于4-bit 权重量化也是如此。 尽管性能有所提高,但上述公式不能广泛应用于权重舍入,主要有两个原因:
- 计算Hessian矩阵的内存消耗和计算复杂度对于大范围应用不太现实
- QUBO问题是所有NP问题都能在多项式时间复杂度内归遇到的问题