照相机标定【计算机视觉第四章】

目录

相机标定概念

畸变现象 

相机标定常用方法 

1. 传统相机标定法

 2.主动视觉相机标定法

3. 相机自标定法

相机标定步骤：

相机标定原理

基本的坐标系

 畸变参数

 相机标定

 线性标定(最小二乘)

非线性标定 

相机标定具体实现

实现代码

角点精确检测结果:

相机参数结果 

 畸变矫正

 总结

---

相机标定概念

        在图像测量过程以及机器视觉应用中，为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立相机成像的几何模型，这些几何模型参数就是相机参数。在大多数条件下这些参数必须通过实验与计算才能得到，这个求解参数的过程就称之为相机标定（或摄像机标定）。

        目的：求出相机的内、外参数，以及畸变参数。

        作用： 标定相机后可以做两件事：1.是由于每个镜头的畸变程度各不相同，通过相机标定可以校正这种镜头畸变矫正畸变，生成矫正后的图像；2.是根据获得的图像重构三维场景。

畸变现象 

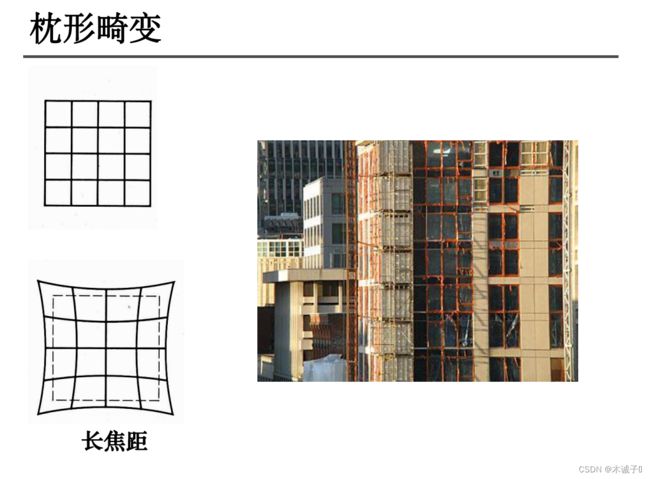
        畸变（distortion）是对直线投影（rectilinear projection）的一种偏移。简单来说直线投影是场景内的一条直线投影到图片上也保持为一条直线。畸变简单来说就是一条直线投影到图片上不能保持为一条直线了，这是一种光学畸变（optical aberration）,可能由于摄像机镜头的原因。

        畸变一般可以分为：径向畸变、切向畸变

        1、径向畸变来自于透镜形状
        2、切向畸变来自于整个摄像机的组装过程

        畸变还有其他类型的畸变，但是没有径向畸变、切向畸变显著

相机标定常用方法 

1. 传统相机标定法

优点：适用任意摄像机模型，标定精度高；

不足：需标定参照物，某些应用中难以实现；

传统相机标定法需要使用尺寸已知的标定物，通过建立标定物上坐标已知的点与其图像点之间的对应，利用一定的算法获得相机模型的内外参数。根据标定物的不同可分为三维标定物和平面型标定物。三维标定物可由单幅图像进行标定，标定精度较高，但高精密三维标定物的加工和维护较困难。平面型标定物比三维标定物制作简单，精度易保证，但标定时必须采用两幅或两幅以上的图像。传统相机标定法在标定过程中始终需要标定物，且标定物的制作精度会影响标定结果。同时有些场合不适合放置标定物也限制了传统相机标定法的应用。

 2.主动视觉相机标定法

        优点：算法简单，往往能够获得线性解，故鲁棒性较高；

        缺点：系统的成本高、实验设备昂贵、实验条件要求高，而且不适合于运动参数位置或无法控制的场合。

       基于主动视觉的相机标定法是指已知相机的某些运动信息对相机进行标定。该方法不需要标定物，但需要控制相机做某些特殊运动，利用这种运动的特殊性可以计算出相机内部参数。

3. 相机自标定法

        优点：自标定方法灵活性强，可对相机进行在线定标；

        缺点：它是基于绝对二次曲线或曲面的方法，其算法鲁棒性差。

        目前出现的自标定算法中主要是利用相机运动的约束。相机的运动约束条件太强，因此使得其在实际中并不实用。利用场景约束主要是利用场景中的一些平行或者正交的信息。其中空间平行线在相机图像平面上的交点被称为消失点，它是射影几何中一个非常重要的特征，所以很多学者研究了基于消失点的相机自标定方法。

相机标定步骤：

1、打印一张棋盘格，把它贴在一个平面上，作为标定物。
2、通过调整标定物或摄像机的方向，为标定物拍摄一些不同方向的照片。
3、从照片中提取棋盘格角点。
4、估算理想无畸变的情况下，五个内参和六个外参。
5、应用最小二乘法估算实际存在径向畸变下的畸变系数。
6、极大似然法，优化估计，提升估计精度。

相机标定原理

        相机标定指建立相机图像像素位置与场景点位置之间的关系，根据相机成像模型，由特征点在图像中坐标与世界坐标的对应关系，求解相机模型的参数。相机需要标定的模型参数包括内部参数和外部参数。
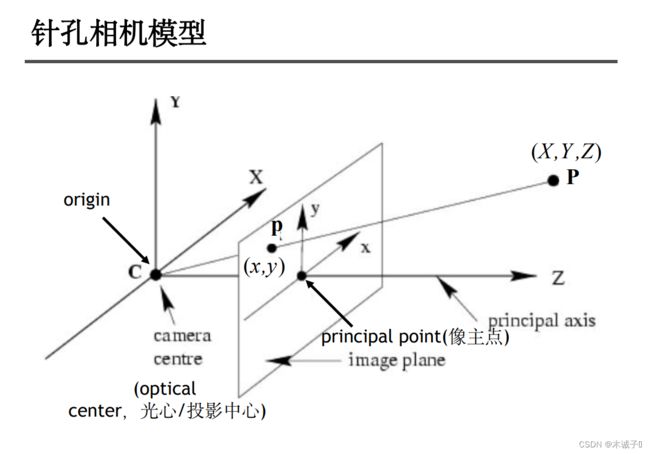
        针孔相机成像原理其实就是利用投影将真实的三维世界坐标转换到二维的相机坐标上去，其模型示意图如下图所示：

基本的坐标系

世界坐标系：用户定义的三维世界的坐标系，为了描述目标物在真实世界里的位置而被引入。

相机坐标系：在相机上建立的坐标系，为了从相机的角度描述物体位置而定义，作为沟通世界坐标系和图像/像素坐标系的中间一环。

图像坐标系：为了描述成像过程中物体从相机坐标系到图像坐标系的投影透射关系而引入，方便进一步得到像素坐标系下的坐标。

一般来说，标定的过程分为两个部分：
第一步是从世界坐标系转换为相机坐标系，这一步是三维点到三维点的转换，包括 R RR，t tt（相机外参）等参数；

        第二步是从相机坐标系转为图像坐标系，这一步是三维点到二维点的转换，包括 K KK（相机内参）等参数；

         同步标定内部参数和外部参数，一般包括两种策略s:光学标定: 利用已知的几何信息(如定长棋盘格)实现参数求解。自标定: 在静态场景中利用 structure from motion估算参数 

 畸变参数

 理想的小孔成像模型，物和像满足相似三角形的关系。实际上由于相机光学系统制造工艺的误差，实际成像与理想成像存在几何失真，称为畸变。畸变主要分为径向畸变和切向畸变。
(1)径向畸变（枕形、桶形）：
①透镜质量原因
②光线在远离透镜中心的地方比靠近中心的地方更加弯曲。

 

径向畸变可以用如下公式修正： 

 

(2)切向畸变（薄透镜畸变和离心畸变）：
切向畸变是由于透镜制造上的缺陷使得透镜本身与图像平面不平行而产生的。
切向畸变可以用如下公式修正： 

 

  

 相机标定

    

 

 

 线性标定(最小二乘)

 线性标定不考虑相机的畸变而只考虑空间坐标转换。
每个坐标点有X,Y两个变量，可列两个方程，相机内参有5个未知数，外参平移和旋转各3个，共有11个变量，因此至少需要6个特征点来求解。

  

可得：

可变得 

可以表示为矩阵形式： 

便可用最小二乘法求解。

给定超定方程（超定方程组是指方程个数大于未知量个数的方程组。对于方程组R a RaRa=y yy，R为n × m n×mn×m矩阵，如果R RR列满秩，且n>m。则方程组没有精确解，此时称方程组为超定方程组）：A x=b
其中x的解为等式两边的误差平方和最小化。

非线性标定 

当镜头畸变明显时必须引入畸变模型，将线性标定模型转化为非线性标定模型，

通过非线性优化的方法求解相机参数：
用概率的视角去看最小二乘问题

 特征点投影方程为

 给定{(ui,vi)}，标定参数矩阵 M MM 的概率为：

 

给定{(ui,vi)}，标定参数矩阵 M 的似然函数为： 

相应求解策略: 牛顿方法、高斯-牛顿方法、Levenberg-Marquardt算法等

相机标定具体实现

 标定所用棋盘格图像集合

  

实现代码

import cv2
import numpy as np
import glob

# 找棋盘格角点
# 设置寻找亚像素角点的参数，采用的停止准则是最大循环次数30和最大误差容限0.001
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001) # 阈值
#棋盘格模板规格
w = 9   # 10 - 1
h = 6   # 7  - 1
# 世界坐标系中的棋盘格点,例如(0,0,0), (1,0,0), (2,0,0) ....,(8,5,0)，去掉Z坐标，记为二维矩阵
objp = np.zeros((w*h,3), np.float32)
objp[:,:2] = np.mgrid[0:w,0:h].T.reshape(-1,2)
objp = objp*18.1  # 18.1 mm

# 储存棋盘格角点的世界坐标和图像坐标对
objpoints = [] # 在世界坐标系中的三维点
imgpoints = [] # 在图像平面的二维点
#加载pic文件夹下所有的jpg图像
images = glob.glob('image/*.jpg')  #   拍摄的十几张棋盘图片所在目录

i=0
for fname in images:

    img = cv2.imread(fname)
    # 获取画面中心点
    #获取图像的长宽
    h1, w1 = img.shape[0], img.shape[1]
    gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
    u, v = img.shape[:2]
    # 找到棋盘格角点
    ret, corners = cv2.findChessboardCorners(gray, (w,h),None)
    # 如果找到足够点对，将其存储起来
    if ret == True:
        print("i:", i)
        i = i+1
        # 在原角点的基础上寻找亚像素角点
        cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)
        #追加进入世界三维点和平面二维点中
        objpoints.append(objp)
        imgpoints.append(corners)
        # 将角点在图像上显示
        cv2.drawChessboardCorners(img, (w,h), corners, ret)
        cv2.namedWindow('findCorners', cv2.WINDOW_NORMAL)
        cv2.resizeWindow('findCorners', 640, 480)
        cv2.imshow('findCorners',img)
        cv2.waitKey(200)
cv2.destroyAllWindows()
#%% 标定
print('正在计算')
#标定
ret, mtx, dist, rvecs, tvecs = \
    cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)

# mtx：内参数矩阵
# dist：畸变系数
# rvecs：旋转向量 （外参数）
# tvecs ：平移向量 （外参数）
print(("ret:"), ret)
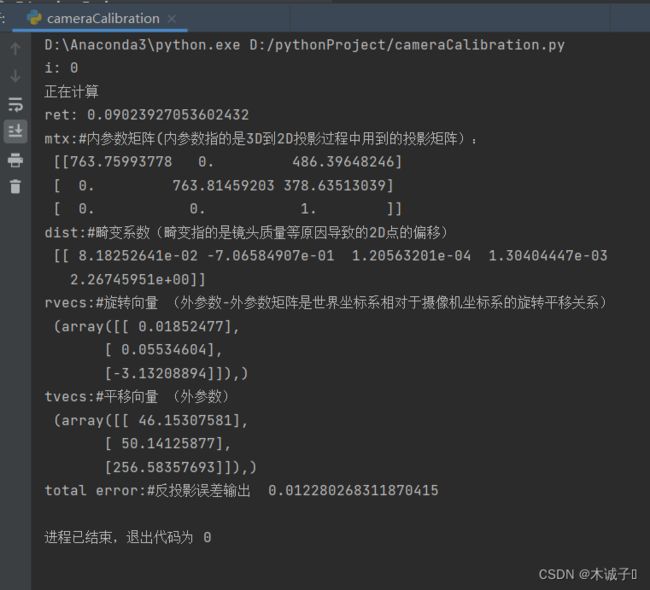
print(("mtx:#内参数矩阵(内参数指的是3D到2D投影过程中用到的投影矩阵）：\n"), mtx)  # 内参数矩阵
print(("dist:#畸变系数（畸变指的是镜头质量等原因导致的2D点的偏移）\n"), dist)  # 畸变系数   distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print(("rvecs:#旋转向量 （外参数-外参数矩阵是世界坐标系相对于摄像机坐标系的旋转平移关系）\n"), rvecs)  # 旋转向量  # 外参数
print(("tvecs:#平移向量 （外参数）\n"), tvecs)  # 平移向量  # 外参数
# 去畸变
img2 = cv2.imread('image/7.jpg')
h, w = img2.shape[:2]
# 我们已经得到了相机内参和畸变系数，在将图像去畸变之前，
# 我们还可以使用cv.getOptimalNewCameraMatrix()优化内参数和畸变系数，
# 通过设定自由自由比例因子alpha。当alpha设为0的时候，
# 将会返回一个剪裁过的将去畸变后不想要的像素去掉的内参数和畸变系数；
# 当alpha设为1的时候，将会返回一个包含额外黑色像素点的内参数和畸变系数，并返回一个ROI用于将其剪裁掉
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx, dist, (w, h), 0, (w, h))  # 自由比例参数

dst = cv2.undistort(img2, mtx, dist, None, newcameramtx)
# 根据前面ROI区域裁剪图片
# x, y, w, h = roi
# dst = dst[y:y + h, x:x + w]
cv2.imwrite('image/calibresult.jpg', dst)

# 反投影误差
# 通过反投影误差，我们可以来评估结果的好坏。越接近0，说明结果越理想。
# 通过之前计算的内参数矩阵、畸变系数、旋转矩阵和平移向量，使用cv2.projectPoints()计算三维点到二维图像的投影，
# 然后计算反投影得到的点与图像上检测到的点的误差，最后计算一个对于所有标定图像的平均误差，这个值就是反投影误差。
total_error = 0
for i in range(len(objpoints)):
    imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
    error = cv2.norm(imgpoints[i], imgpoints2, cv2.NORM_L2) / len(imgpoints2)
    total_error += error
print(("total error:#反投影误差输出 "), total_error / len(objpoints))

角点精确检测结果:

相机参数结果 

 畸变矫正

我们已经得到了相机内参和畸变系数，在将图像去畸变之前，我们还可以使用cv.getOptimalNewCameraMatrix()优化内参数和畸变系数，通过设定自由自由比例因子alpha。当alpha设为0的时候，将会返回一个剪裁过的将去畸变后不想要的像素去掉的内参数和畸变系数；当alpha设为1的时候，将会返回一个包含额外黑色像素点的内参数和畸变系数，并返回一个ROI用于将其剪裁掉。

原图

 矫正后

 总结

     相机标定方法有：传统相机标定法、主动视觉相机标定方法、相机自标定法。

传统相机标定法需要使用尺寸已知的标定物，通过建立标定物上坐标已知的点与其图像点之间的对应，利用一定的算法获得相机模型的内外参数。根据标定物的不同可分为三维标定物和平面型标定物。三维标定物可由单幅图像进行标定，标定精度较高，但高精密三维标定物的加工和维护较困难。平面型标定物比三维标定物制作简单，精度易保证，但标定时必须采用两幅或两幅以上的图像。传统相机标定法在标定过程中始终需要标定物，且标定物的制作精度会影响标定结果。同时有些场合不适合放置标定物也限制了传统相机标定法的应用。

        目前出现的自标定算法中主要是利用相机运动的约束。相机的运动约束条件太强，因此使得其在实际中并不实用。利用场景约束主要是利用场景中的一些平行或者正交的信息。其中空间平行线在相机图像平面上的交点被称为消失点，它是射影几何中一个非常重要的特征，所以很多学者研究了基于消失点的相机自标定方法。自标定方法灵活性强，可对相机进行在线定标。但由于它是基于绝对二次曲线或曲面的方法，其算法鲁棒性差。

       基于主动视觉的相机标定法是指已知相机的某些运动信息对相机进行标定。该方法不需要标定物，但需要控制相机做某些特殊运动，利用这种运动的特殊性可以计算出相机内部参数。基于主动视觉的相机标定法的优点是算法简单，往往能够获得线性解，故鲁棒性较高，缺点是系统的成本高、实验设备昂贵、实验条件要求高，而且不适合于运动参数未知或无法控制的场合。

常用术语

• 内参矩阵: Intrinsic Matrix
• 焦距: Focal Length
• 主点: Principal Point
• 径向畸变: Radial Distortion
• 切向畸变: Tangential Distortion
• 旋转矩阵: Rotation Matrices
• 平移向量: Translation Vectors
• 平均重投影误差: Mean Reprojection Error
• 重投影误差: Reprojection Errors
• 重投影点: Reprojected Points