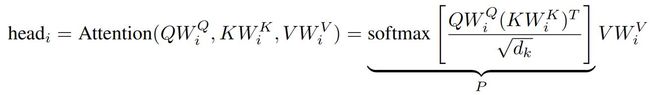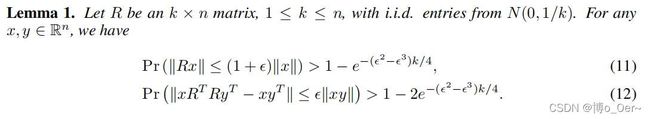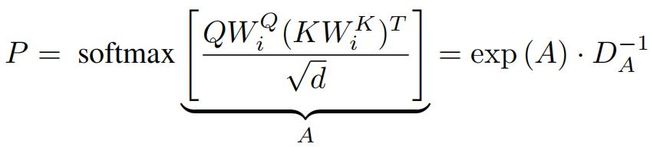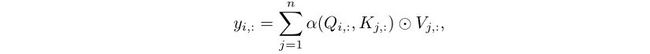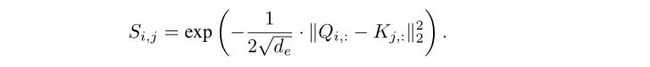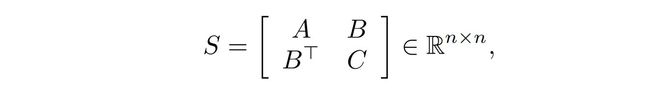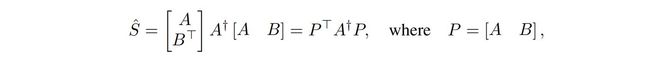论文笔记 -- SOFT: Softmax-free Transformer with Linear Complexity
文章目录
- SOFT: Softmax-free Transformer with Linear Complexity
-
- Background
- Motivation
-
- 投影相关工作
- Contribution
- Related work
-
- 对于自注意力矩阵为低秩矩阵的证明
- Model
-
- Softmax-free self-attention步骤
- 注意力矩阵的低秩正则化
- Experiment
-
- 使用 S ^ \hat S S^构建Transformer模型
- 自身实验方法
- 对比试验
SOFT: Softmax-free Transformer with Linear Complexity
原文: SOFT: Softmax-free Transformer with Linear Complexity
出处: NeurIPS-2021 (Neural Information Processing Systems)
摘要: ViT通过图像块序列化+自注意力机制将不同CV任务性能往前推了一把。然而,自注意力机制会带来更高的计算复杂度与内存占用。在NLP领域已有不同的方案尝试采用线性复杂度对自注意力进行近似。然而,本文的深入分析表明:NLP中的近似方案在CV中缺乏理论支撑或者无效。进一步分析了其局限性根因:softmax self-attention 。具体来说,传统自注意力通过计算token之间的点乘并归一化得到自注意力。softmax操作会对后续的线性近似带来极大挑战。基于该发现,本文首次提出了SOFT(softmax-free transformer )。为移除自注意力中的softmax,采用高斯核函数替代点乘相似性且无需进一步的归一化。这就使得自注意力矩阵可以通过低秩矩阵分析近似 。近似的鲁棒性可以通过计算其MP逆(Moore-Penrose Inverse)得到。SOFT的线性复杂度可以允许更长的token序列,进而取得更佳的精度-复杂度均衡。
核心思想:使用高斯核函数代替softmax计算内积,能够通过低秩矩阵分解来近似得到 self-attention 矩阵
Background
- 在视觉领域,基于self-attention的transformer虽然取得了较好的效果,但其计算量和内存都和是输入分辨率大小的平方
- 研究认为这种复杂的计算限制主要来源于计算概率时使用的softmax self-attention
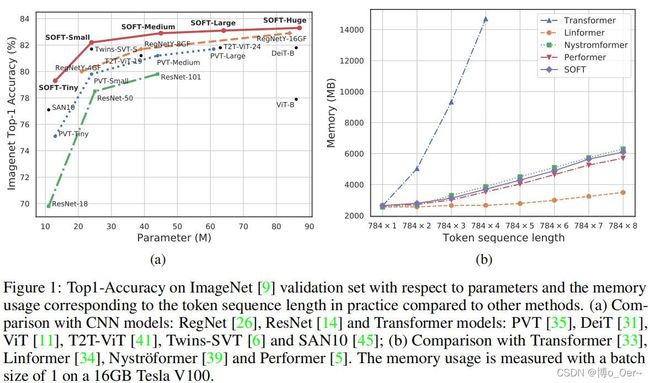
**首先通过实验证明:**实际应用在ImageNet验证集上,token序列长度对应的参数和内存使用量方面的精确度最高的方法;(a) 与CNN系列方法相比;(b) 与Transformer系列方法相比
Motivation
-
在Vision Transformers(ViTs)上受自注意力的二次复杂度影响高于NLP任务,这一问题随着图像分辨率的提高愈发明显
对于自然语言处理和时间序列表示,所处理的数据为向量形式(数据规模为 n ∗ 1 n*1 n∗1),视觉所处理的数据为矩阵形式(数据规模为 n ∗ n n*n n∗n)。这样在transformer的 O ( n 2 ) O(n^2) O(n2)复杂度情况下对视觉任务的影响更大
-
在NLP任务对于自注意力复杂度的降低方式之一为引入 W q , Q k , W v W_q, Q_k, W_v Wq,Qk,Wv矩阵将 Q , K , V Q,K,V Q,K,V投影到一个低维空间(乘以权重矩阵可以避免self-attention退化成一个point-wise线性映射,注意力矩阵变为一个对称矩阵,并且达到 Q , K , V Q,K,V Q,K,V表示的降维)
投影相关工作
Reformer: The Efficient Transformer将 Q , K , V Q,K,V Q,K,V设置为相同的值并且没有进行投影,目的为减少模型参数**(主要思想为使用局部敏感的哈希注意力(LSH)代替自注意力操作)**通过哈希映射找query近邻key,去代替原来所有的key进行注意力计算,不设置权重矩阵是为了适应LSH
Contribution
- 此前的工作对于Transformer的改进没有考虑softmax的影响,本文使用高斯核函数代替softmax提出一种新颖的线性空间、时间复杂度 的softmax-free Transformer(复杂度为 O ( n ) O(n) O(n))
- 所提注意力矩阵近似可以通过具有理论保证(低秩矩阵分解)的矩阵分解算法 计算得到
- SOFT在ImageNet图像分类任务上取得了比其他ViT方案更佳的精度-复杂度均衡
Related work
本文的主要思想为使用高斯核函数代替softmax,并利用低秩矩阵分解实降低复杂度
对于自注意力矩阵为低秩矩阵的证明
Linformer: Self-Attention with Linear Complexity文章指出Self-Attention is Low Rank
每个注意力头表示为:
P P P为上下文映射矩阵,证明 P P P是一个低秩矩阵
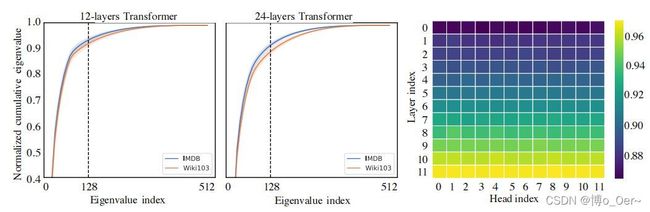
通过使用预训练模型RoBERTa-base进行上下文映射矩阵频谱分析的实验证明:
- 实验不同注意力头的 P P P矩阵做奇异值分解,得出注意力的分布符合长尾分布
- 在奇异值的热图中,高层的谱分布比下层更倾斜,这意味着在高层,更多的信息集中在最大的奇异值上
这就意味着上下文映射矩阵的大部分信息可以从少量的信息集中的奇异值中恢复,并且从实验的层面证明了上下文映射矩阵是一个低秩矩阵
使用的引理为:Johnson–Lindenstrauss lemma
首先将上下文映射矩阵 P P P写成另一种形式:
其中 D A D_A DA是一个 n × n n\times n n×n的对角矩阵,构造的近似低秩矩阵为:
P ~ = exp ( A ) ⋅ D A − 1 R T R \tilde P=\exp(A)\cdot D_{A}^{-1}R^TR P~=exp(A)⋅DA−1RTR
R R R为根据JL引理构造,其中 R ∈ R n R\in \mathbb R^n R∈Rn来自于 N ( 0 , 1 / k ) N(0,1/k) N(0,1/k),根据JL引理,对于矩阵 V W i V VW_{i}^{V} VWiV的任意列向量 ω ∈ R n \omega \in \mathbb R^n ω∈Rn,当 k = 5 log ( n ) / ( ϵ 2 − ϵ 3 ) k=5\log (n)/(\epsilon^2-\epsilon^3) k=5log(n)/(ϵ2−ϵ3)时可以得到:
P r ( ∣ ∣ P R T R ω T − P ω T ∣ ∣ ≤ ϵ ∣ ∣ P ~ ω T ∣ ∣ ) > 1 − o ( 1 ) Pr(||PR^TR\omega^T-P\omega^T||\leq\epsilon||\tilde P\omega^T||)>1-o(1) Pr(∣∣PRTRωT−PωT∣∣≤ϵ∣∣P~ωT∣∣)>1−o(1)
**解释:**低秩矩阵 P ~ \tilde P P~可以在一定精确度 ϵ \epsilon ϵ的约束下近似 P P P,并保证信息的保留在概率 1 − o ( 1 ) 1-o(1) 1−o(1)以上
Model
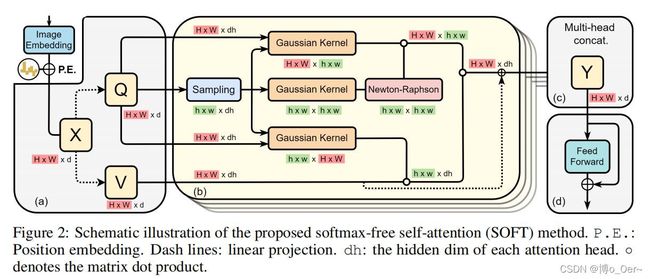
Softmax-free self-attention步骤
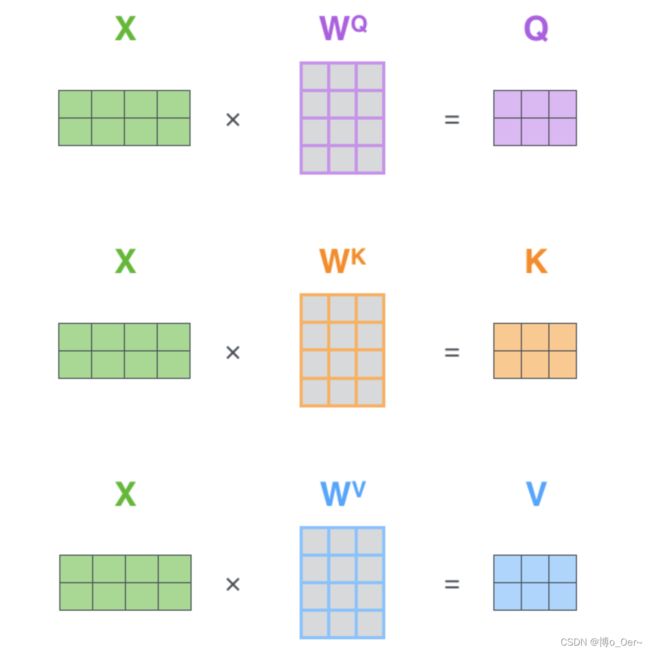
给定 n n n个token序列 X ∈ R n × d X\in\mathbb R^{n\times d} X∈Rn×d,每个token由一个 d d d维向量表示
Attention的输入形式为:
![]()
自注意力矩阵的一种通用表示方法为:
其中 ⨀ \bigodot ⨀为哈达玛积(Hadamard product),即对于位置矩阵元素相乘; α \alpha α是注意力机制的关键方程,由一个非线性方程和一个关系方程组成,组成 α \alpha α的两块为:
该项研究引入了一个用高斯核函数代替自注意力机制中的点积:
得到的最终形式为:
可以看到,式中使用的高斯核函数为一个二范数
对于这种新的自注意力的表现形式,好处在于:
- 得到的自注意力矩阵 S S S为对称矩阵
- 所有元素的范围为 [ 0 , 1 ] [0,1] [0,1]
- 对角线上的元素最大值都为1,其余元素按照相关性映射到 [ 1 , 1 ] [1,1] [1,1]区间
注意力矩阵的低秩正则化
**上诉方法存在的问题:**在使用基于高斯核的自注意力矩阵 S S S而不进行线性化时,transformer的训练不能够收敛(但是使用点积自注意力时可以收敛。这就解释了点积softmax self-attention为什么广泛使用)
为了解决收敛性问题和二次复杂度问题,使用Nyström对注意力矩阵进行低秩正则化,这样做的好处是使得模型复杂度大幅度下降,且无需计算全部的自注意力矩阵
使用 S = exp ( Q ⊖ K ) S=\exp(Q\ominus K) S=exp(Q⊖K)表示如下分块矩阵:
其中:
![]()
通过Nyström分解可表示为, A + A^+ A+为 A A A的广义逆矩阵:
在标准Nyström中,A和B是S通过随机采样m个token得到的子矩阵,记为 Q ~ \widetilde Q Q ,称为bottleneck tokens
根据经验判断存在的问题为:随机抽样对于 m m m的选择相当敏感,探索的解决方案为:
- 使用核大小为k,步幅为k的一个卷积层学习 Q ~ \widetilde Q Q
- 使用核大小为k,步幅为k的平均池化生成 Q ~ \widetilde Q Q
通过实验发现第一种方案效果更好,所以在计算时默认使用第一种方案。由于K和Q相同,则 Q ~ = K ~ \widetilde Q=\widetilde K Q =K , A A A和 P P P的表示如下:
最终的SOFT正则化自注意力矩阵可以表示为如下形式:
Experiment
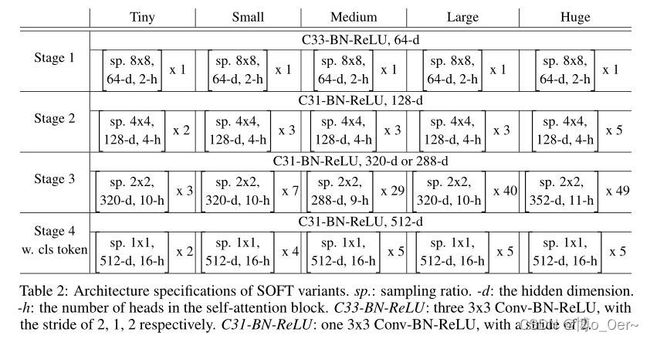
使用 S ^ \hat S S^构建Transformer模型
sp:抽样比例
-d:隐藏维度
-h:在自我注意块中的头数
C33-BN-ReLU:三个3*3的Conv-BN-ReLU,步幅跨度为2、1、2
C31-BN-ReLU:一个3*3的Conv-BN-ReLU,步幅跨度为2
自身实验方法
先使用权重衰减为0.05的10次迭代作为linear warm-up,之后使用AdamW作为优化器进行300论训练,在训练过程中,采用randomflip、mixup和cutmix进行数据增强,使用Label smoothing进行损失函数计算。
对比试验
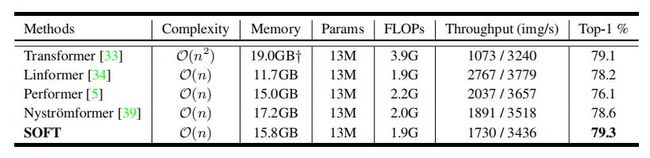
与Transformer系列方法的比较:
复杂度比较:
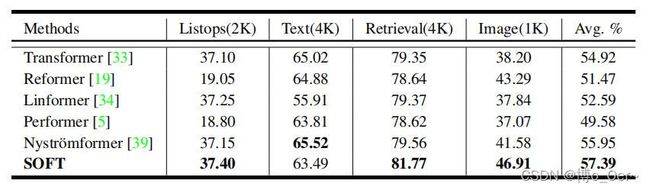
模型性能比较:
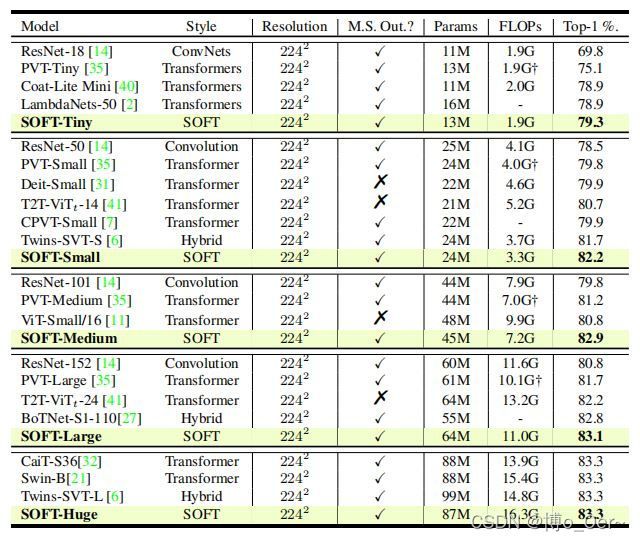
与用于计算机视觉的CNNs和ViTs的对比: