2016_ICLR-Session-based recommendations with recurrent neural networks阅读笔记

基于序列的循环神经网络推荐系统

session-based 的概念：
session是服务器端用来记录识别用户的一种机制。典型的场景比如购物车，服务端为特定的对象创建了特定的Session，用于标识这个对象，并且跟踪用户的浏览点击行为。这里可以将其理解为具有时序关系的一些记录序列。
可以理解为从进入某个app直到退出的全过程中，根据用户的行为变化所发生的推荐，此时session是从进入app到退出app的全过程；也可以理解为根据用户某段时间内的行为序列发生的推荐，此时session不一定是从进入app到退出的全过程，比如airbnb的论文中，只要前后两次的点击不超过30min，都算作同一个session。

基于物品的协同过滤 指根据用户对物品的行为数据来计算物品与物品之间的相似度，为用户推荐喜欢的物品相似的物品，例如：如果一个用户喜欢物品A的同时也喜欢物品B那么就认为物品A与物品B相似；

基于用户的协同过滤 指通过物品对用户的行为数据来计算用户与用户的相似度，为用户推荐相似用户喜欢的物品。协同过滤在能够进行高质量推荐之前需要大量的历史数据，面临着冷启动问题。

写作动机

实时推荐系统常常面临只能依靠短序列建模而不是长的用户历史数据的问题。
在实际中通常使用item-to-item推荐方法（建立item to item的相似度矩阵）来解决，比如当用户在一个session中点击了某一个物品时，基于相似度矩阵得到相似的物品推荐给用户。这种方法简单有效，并被广泛应用，但是这种推荐方法只考虑了用户的最后一次点击，实际上忽略了过去的点击（clicks）信息。
另一种方法是利用马尔可夫决策过程（MDPs）进行推荐，
本文提出对整个序列建模可以提供更精准的推荐。其主要学习的是状态转移概率，即点击了物品A之后，下一次点击的物品是B的概率，并基于这个状态转移概率进行推荐。这样的缺陷主要是随着物品的增加，建模用户所有的可能的点击序列变得难以管控。
General Factorization Framework (GFF) 方法用事件（event）之和来建模会话（session），用item本身的特征表达以及item作为会话的一部分的表达的平均值作为潜在表达（latent representation）。但是这种方法没有考虑会话中的事件的顺序信息。
本文提出的模型是基于RNN的方法来进行基于会话的推荐，我们可以称之为GRU4Rec模型。

模型介绍

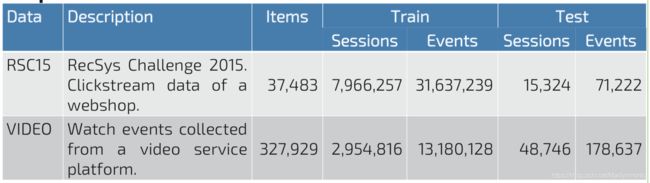
模型结构如下：
输入： 依次输入一个session的点击序列$x=[x_1,x_2...x_{r-1},x_r],1\le r\le n$。
序列中的每一个 $x_i,x_i\in x$ 表示成独热编码，随后通过embedding层压缩为低维连续向量作为 GRU 单元的输入。
输出： 预测每一个item被点击的预测概率$y=M(x),wherey=[y_1,y_2...y_m]$，其中概率最大的$y_j$为预测的下一个被点击的item。
GRU层： RNN效果不佳，LSTM同准确度下速度更慢
Embedding层和 Feedforward层： 可选项
GRU层数： 层数为1时效果最佳；会话跨越较短的时间框架；不需要多尺度建模。

将模型与RecSys任务融合

为了提高模型训练的效率，修改训练策略使GRU适用于RecSys任务。

Trick1: Session parallel mini-batches

提出该trick的动机：
1）会话长度差异很大，例如$sessio{n}_1$包含2个事件，而$sessio{n}_2$可能包含100个事件；
2）捕捉会话随时间的演变过程。

具体策略：

• 将所有的会话排序(随机排序或按照时间排序)；
• 前X个会话中，每个会话的第一个事件组成第一个输入的Mini-batch1(X为mini-batch的尺寸Batch-Size)；
• 前X个会话中，每个会话的第二个事件为第一个输入的Mini-batch的期望输出；依此类推，第二个Mini-batch(输入)则由第二个事件组成，(期望输出)则由第三个事件组成；当某个会话结束时，将下一个可用会话放在其位置。由于Session之间是独立的，需要重置相应的GRU中的隐藏状态。

如图所示，Session1的长度为4，Session2的长度为2，Session3的长度为6，Session4的长度为2，Session5的长度为3。假设Batch-Size为3，那么我们首先用前三个Session进行训练，不过当训练到第三个物品时，Session2已经结束了，那么我们便将Session4来接替上，不过这里要注意将GRU中的状态重新初始化。

Trick2: Sampling the output

提出该trick的动机：
1）item的数量通常很多(十万甚至上百万个)；
2）训练规模=事件数 * hidden layer层数 * 输出维度(等于item总数)，为$O(N_{E}H{N}_I)$
3）item样本和用户行为的变化很快，需要频繁地训练模型。

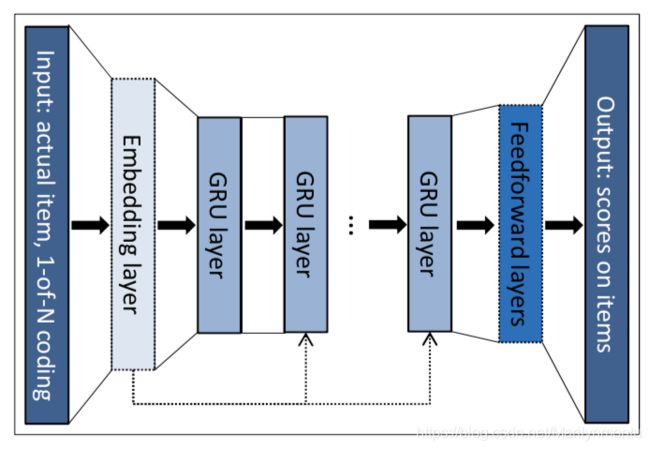
具体策略：

• 对于输入，期望的输出是一个关于所有item的one-hot向量；
• 计算期望的输出（即desired items）的得分；
• 基于受欢迎程度进行抽样：某个事件没有点击更受欢迎的item，则说明该item很大可能是负反馈；
• 使用同一mini-batch中的其他item作为当前事件的负样本。这是一种在实际上有效果的机遇受欢迎程度的采样方法。

图中$i_1$为对应某输入的正样本，$i_5$和$i_8$则为负样本。

Pairwise ranking loss function

动机：

• 推荐系统的目的是对item进行排序 (ranking)；
• 单文档法(pointwise ranking)和文档对法(pairwise ranking)已被广泛应用，而文档列表 (listwise-ranking)的可扩展性差；
• 文档对法效果通常更好。

方法：

• BPR(Adapt Bayesian Personalized Ranking):
  对比正样本和每个负样本的点击概率值，若正样本的点击概率大于负样本的点击概率，这样损失会比较小，若正样本的点击概率小于负样本，损失会比较大。
  
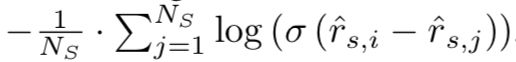
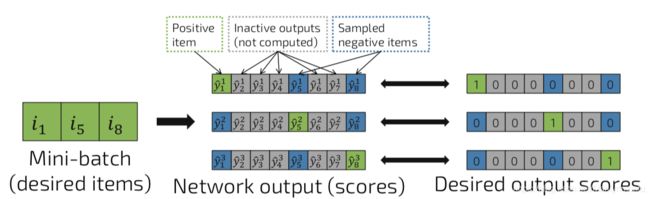
• TOP1(presented):
  该排名损失是本文为推荐任务设计的，它是期望item的相对排序的正则逼近。相关item的相对排名为：
  
  式中，$I\{\cdot \}$为sigmoid函数，$N_S$为一个Mini_batch中的Session总数，即batch_size。
  为了防止正负样本间差异很小导致负样本分数偏高的情况，因此增加正则化项使负样本的分数尽可能接近0。
  
  式中， ${\hat{r}}_{s,i}$是当前时刻在item i(期望的item)上的打分，${\hat{r}}_{s,j}$是当前时刻在item j(负样本)上的打分。

此处引用文哥的一段原文：
好了，最后我们来讨论一下我阅读本文时最为疑虑的地方吧，为什么使用pair-wise的损失函数，要比point-wise的损失函数更好呢？这主要还是看场景吧。比如在电商领域、外卖点餐的时候，我们可能很多东西都喜欢，但是只会挑选一个最喜欢的物品进行点击或者购买。这种情况下并不是一个非黑即白的classification问题，只是说相对于某个物品，我们更喜欢另一个物品，这时候更多的是体现用户对于不同物品的一个相对偏好关系，此时使用pair-wise的损失函数效果可能会好一点。在广告领域，一般情况下用户只会展示一个广告，用户点击了就是点击了，没点击就是没点击，我们可以把它当作非黑即白的classification问题，使用point-wise的损失函数就可以了。
不过还是要提一点，相对于使用point-wise的损失函数，使用pair-wise的损失函数，我们需要采集更多的数据，如果在数据量不是十分充足的情况下，point-wise的损失函数也许是更合适的选择。

实验

数据集：

评价指标：

• recall@20:
  该指标是期望的item在模型输出的分数排名前20的个数(不考虑具体的排名)。
• MRR@20:
  该指标是期望的item在模型输出的分数中的排序的倒数，其后对所有事件取平均可得。排名大于20时，MRR=0。

Baseline：

• POP：推荐训练集中最受欢迎的item
• S-POP：推荐当前session中最受欢迎的item
• Item-KNN：推荐与实际item相似的item，相似度被定义为session向量之间的余弦相似度
• BPR-MF：一种矩阵分解法，新会话的特征向量为其内的item的特征向量的平均，把它作为用户特征向量。

实验结果：

• 效果最好的Baseline为Item-KNN
  
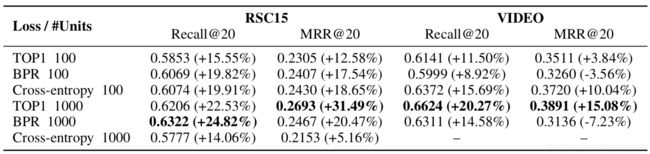
• 通过在随机选取的参数空间点对每个数据集和损失函数进行100个实验，对超参数进行了优化。得出的最佳参数如下表。
  
• 实验得出单层GRU的效果最佳，下图为分别改变单层GRU的节点数及损失函数的实验结果。
• 表中数据为相对于最佳的Baseline(Item-KNN)的Recall@20和MRR@20两个评价指标的增长。
• 可以看到，使用point-wise的交叉熵损失函数不稳定。使用文中提出的两种Rank Loss相较于使用point-wise的交叉熵损失函数，模型的推荐效果有了较大的提升。
  
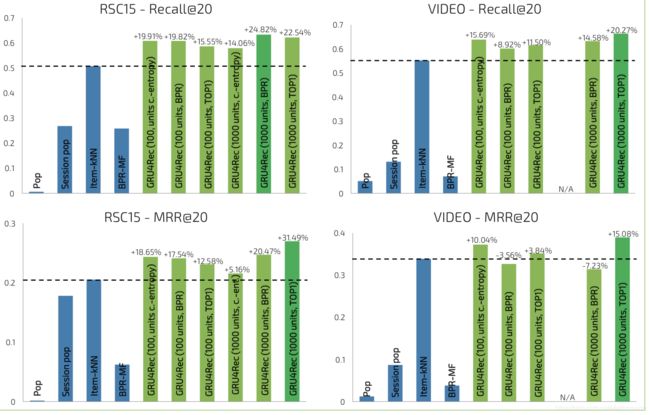
• 将表格转换为柱形图更为直观，可见基于RNN的推荐算法效果显著。
  

参考链接：

论文下载地址为：http://arxiv.org/abs/1511.06939
文哥的学习日记：https://www.jianshu.com/p/9a4b3791fda2
原文代码地址：https://github.com/hidasib/GRU4Rec
tf参考代码地址：https://github.com/princewen/tensorflow_practice/tree/master/recommendation/Basic-SessionBasedRNN-Demo
python2代码地址：https://github.com/Songweiping/GRU4Rec_TensorFlow