(五)OpenCV | 斑点中心检测(图像矩)
文章目录
- 1. 图像矩
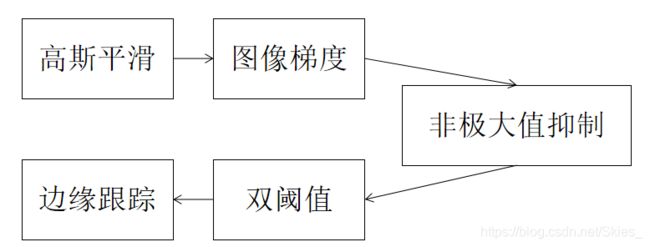
- 2. Canny边缘检测
-
- 2.1 高斯平滑
- 2.2 图像梯度
- 2.3 非极大值抑制
- 2.4 双阈值
- 2.5 边缘跟踪
- 参考
1. 图像矩
前一文介绍了斑点的检测,本文将介绍斑点中心的检测,主要用到了OpenCV中图像矩的概念。图像矩不仅可以描述图像的全局特征,还可以提供大量如图像大小、位置、方向和形状等图像信息。OpenCV中图像矩的计算定义在类Moments中,其部分源码为:
Moments(double m00, double m10, double m01, double m20, double m11,
double m02, double m30, double m21, double m12, double m03);
// spatial moments
CV_PROP_RW double m00, m10, m01, m20, m11, m02, m30, m21, m12, m03;
// central moments
CV_PROP_RW double mu20, mu11, mu02, mu30, mu21, mu12, mu03;
// central normalized moments
CV_PROP_RW double nu20, nu11, nu02, nu30, nu21, nu12, nu03;
首先是空间矩。其中, i + j i+j i+j 阶矩的计算公式如下: m i j = ∑ x , y a r r a y ( x , y ) ⋅ x i ⋅ y j (1) {\rm m}_{ij}=\sum_{x,y}array(x,y)\cdot x^i\cdot y^j\tag{1} mij=x,y∑array(x,y)⋅xi⋅yj(1)
这里,对于二值图像来说, a r r a y ( x , y ) array(x,y) array(x,y) 为 0 0 0 或 1 1 1。则零阶矩 m 00 \rm m_{00} m00 表示该二值图像的非零像素点数量,易得该值与轮廓所在位置无关;一阶矩 m 01 \rm m_{01} m01 和 m 10 \rm m_{10} m10 分别表示该二值图像的非零像素点横坐标和纵坐标之和,可以反映图像的形状特征。则此时该二值图像对应的质心坐标可以通过下式得到: x ˉ = m 10 m 00 , y ˉ = m 01 m 00 (2) \bar x=\frac{\rm m_{10}}{\rm m_{00}},\ \ \bar y=\frac{\rm m_{01}}{\rm m_{00}}\tag{2} xˉ=m00m10, yˉ=m00m01(2)
同理,可以得到二阶矩和三阶矩,而二阶矩和三阶矩可以进一步得到图像的中心矩和归一化中心矩,统称为不变矩。不变矩可以反映图像的统计特征,其具有旋转、平移、缩放的不变特征。先来看中心矩,其中 i + j i+j i+j 阶中心矩的计算公式如下: m u i j = ∑ x , y a r r a y ( x , y ) ⋅ ( x − x ˉ ) i ⋅ ( y − y ˉ ) j (3) {\rm mu}_{ij}=\sum_{x,y}array(x,y)\cdot(x-\bar x)^i\cdot(y-\bar y)^j\tag{3} muij=x,y∑array(x,y)⋅(x−xˉ)i⋅(y−yˉ)j(3)
通过上式,易得零阶中心矩等于零阶矩 m 00 \rm m_{00} m00 ,一阶中心距为零。对于更高阶的矩,由于是相对物体质量而得到的,所以它们也不随物体在图像中的绝对位置改变而改变,即中心矩的平移不变性。再来看归一化中心矩,其中 i + j i+j i+j 阶归一化中心矩的计算公式如下: n u i j = m u i j m 00 ( i + j ) / 2 + 1 (4) {\rm nu}_{ij}=\frac{{\rm mu}_{ij}}{\rm m_{00}^{(i+j)/2+1}}\tag{4} nuij=m00(i+j)/2+1muij(4)
归一化中心矩就是在中心矩加上一个归一化因子,这个因子是二值化图像中的非零像素点数量的幂(对于更高阶的矩,这个幂会变大)。中心矩通过减去均值而获得平移不变性,归一化中心矩通过除以物体的总尺寸而获得缩放不变性(当物体缩放时,上式的分子和分母以同等比例缩放)。同时,归一化中心矩也具有平移不变性。
最后,为了叙述的完整性,介绍Hu不变矩。它是归一化中心矩的线性组合。通过组合不同的归一化中心矩,我们可以得到一个反映图像不同特征的不同函数,这个函数不随平移、缩放、旋转等的变化而变化。
h u 1 = n u 20 + n u 02 h u 2 = ( n u 20 + n u 02 ) 2 + 4 n u 11 2 h u 3 = ( n u 30 − 3 n u 12 ) 2 + 3 ( n u 21 − n u 03 ) 2 h u 4 = ( n u 30 + n u 12 ) 2 + ( n u 21 + n u 03 ) 2 h u 5 = ( n u 30 − 3 n u 12 ) ( n u 30 + n u 12 ) [ ( n u 30 + n u 12 ) 2 − 3 ( n u 21 + n u 03 ) 2 ] + ( 3 n u 21 − n u 03 ) ( n u 21 + n u 03 ) [ 3 ( n u 30 + n u 12 ) − ( n u 21 + n u 03 ) ] h u 6 = ( n u 20 − n u 02 ) [ ( n u 30 + n u 12 ) 2 − ( n u 21 + n u 03 ) 2 ] + 4 n u 11 ( n u 30 + n u 12 ) ( n u 21 + n u 03 ) 2 h u 7 = ( 3 n u 21 − n u 03 ) ( n u 30 + n u 12 ) [ ( n u 30 + n u 12 ) 2 − 3 ( n u 21 + n u 03 ) 2 ] − ( n u 30 − 3 n u 12 ) ( n u 21 + n u 03 ) [ 3 ( n u 30 + n u 12 ) 2 − ( n u 21 + n u 03 ) 2 ] (5) \begin{aligned} {\rm hu}_1&={\rm nu}_{20}+{\rm nu}_{02} \\ {\rm hu}_2&=({\rm nu}_{20}+{\rm nu}_{02})^2+4{\rm nu}_{11}^2 \\ {\rm hu}_3&=({\rm nu}_{30}-3{\rm nu}_{12})^2+3({\rm nu}_{21}-{\rm nu}_{03})^2 \\ {\rm hu}_4&=({\rm nu}_{30}+{\rm nu}_{12})^2+({\rm nu}_{21}+{\rm nu}_{03})^2 \\ {\rm hu}_5&=({\rm nu}_{30}-3{\rm nu}_{12})({\rm nu}_{30}+{\rm nu}_{12})\left[({\rm nu}_{30}+{\rm nu}_{12})^2-3({\rm nu}_{21}+{\rm nu}_{03})^2\right] \\ & + (3{\rm nu}_{21}-{\rm nu}_{03})({\rm nu}_{21}+{\rm nu}_{03})\left[3({\rm nu}_{30}+{\rm nu}_{12})-({\rm nu}_{21}+{\rm nu}_{03})\right] \\ {\rm hu}_6&=({\rm nu}_{20}-{\rm nu}_{02})\left[({\rm nu}_{30}+{\rm nu}_{12})^2-({\rm nu}_{21}+{\rm nu}_{03})^2\right]+4{\rm nu}_{11}({\rm nu}_{30}+{\rm nu}_{12})({\rm nu}_{21}+{\rm nu}_{03})^2 \\ {\rm hu}_7&=(3{\rm nu}_{21}-{\rm nu}_{03})({\rm nu}_{30}+{\rm nu}_{12})\left[({\rm nu}_{30}+{\rm nu}_{12})^2-3({\rm nu}_{21}+{\rm nu}_{03})^2\right] \\ & - ({\rm nu}_{30}-3{\rm nu}_{12})({\rm nu}_{21}+{\rm nu}_{03})\left[3({\rm nu}_{30}+{\rm nu}_{12})^2-({\rm nu}_{21}+{\rm nu}_{03})^2\right] \\ \end{aligned}\tag{5} hu1hu2hu3hu4hu5hu6hu7=nu20+nu02=(nu20+nu02)2+4nu112=(nu30−3nu12)2+3(nu21−nu03)2=(nu30+nu12)2+(nu21+nu03)2=(nu30−3nu12)(nu30+nu12)[(nu30+nu12)2−3(nu21+nu03)2]+(3nu21−nu03)(nu21+nu03)[3(nu30+nu12)−(nu21+nu03)]=(nu20−nu02)[(nu30+nu12)2−(nu21+nu03)2]+4nu11(nu30+nu12)(nu21+nu03)2=(3nu21−nu03)(nu30+nu12)[(nu30+nu12)2−3(nu21+nu03)2]−(nu30−3nu12)(nu21+nu03)[3(nu30+nu12)2−(nu21+nu03)2](5)
这里,直接使用一个例子来说明Hu不变矩的平移、旋转、缩放等不变性特征。
#include第二幅图像是第一幅图像平移后的结果;第三幅图像是第一幅图像放大后的结果;第四幅图像是第一幅图像旋转后的结果。
| h u 1 {\rm hu}_1 hu1 | h u 2 {\rm hu}_2 hu2 | h u 3 {\rm hu}_3 hu3 | h u 4 {\rm hu}_4 hu4 | h u 5 {\rm hu}_5 hu5 | h u 6 {\rm hu}_6 hu6 | h u 7 {\rm hu}_7 hu7 | |
|---|---|---|---|---|---|---|---|
| 1 | 0.00130764 | 5.4248e-08 | 2.80186e-11 | 2.15264e-12 | 1.58235e-23 | 2.33778e-16 | -5.39496e-24 |
| 2 | 0.00130711 | 5.43252e-08 | 2.75262e-11 | 2.14713e-12 | 1.55648e-23 | 2.29674e-16 | -5.49622e-24 |
| 3 | 0.00130433 | 5.58127e-08 | 2.67299e-11 | 1.98447e-12 | 1.36036e-23 | 2.17734e-16 | -4.88229e-24 |
| 4 | 0.00130697 | 5.41004e-08 | 2.76969e-11 | 2.03061e-12 | 1.44933e-23 | 2.253e-16 | -4.67461e-24 |
由表可知,在误差范围内,Hu不变矩满足平移、旋转、缩放等特征的不变性。
最后,根据以上知识来求斑点的中心。首先是单个斑点的中心检测:
#include2. Canny边缘检测
2.1 高斯平滑
由于边缘检测易受到图像中噪点的影响,Canny边缘检测第一步首先使用高斯平滑对图像进行降噪处理。大小为 ( 2 k + 1 ) × ( 2 k + 1 ) (2k+1)\times(2k+1) (2k+1)×(2k+1)的高斯核为: H i j = 1 2 π σ 2 exp ( − ( i − ( k + 1 ) ) 2 + ( j − ( k + 1 ) ) 2 2 σ 2 ) ; 1 ≤ i , j ≤ ( 2 k + 1 ) (6) H_{ij}=\frac{1}{2\pi\sigma^2}\exp \left(-\frac{(i-(k+1))^2+(j-(k+1))^2}{2\sigma^2}\right);1\leq i,j\leq(2k+1)\tag{6} Hij=2πσ21exp(−2σ2(i−(k+1))2+(j−(k+1))2);1≤i,j≤(2k+1)(6)
这里,选择高斯核的大小将会影响Canny检测器的性能。一般情况下,高斯核的尺寸越大,检测器对噪点的敏感度越低;但随着高斯核尺寸的增大,边缘检测的误差会增大。
2.2 图像梯度
图像中的边缘可能指向任意方向,Canny检测算法使用四个过滤器来检测水平、垂直和对角线方向的边缘。使用边缘检测算子(OpenCV中使用Sobel算子)得到水平方向和垂直方向的梯度,分别为 G x {\bold G}_x Gx和 G y {\bold G}_y Gy。由此可以确定边缘的梯度和方向: G = G x 2 + G y 2 (7) \bold G=\sqrt{{\bold G}_x^2+{\bold G}_y^2}\tag{7} G=Gx2+Gy2(7)
Θ = arctan ( G y , G x ) (8) \Theta=\arctan({\bold G}_y,{\bold G}_x)\tag{8} Θ=arctan(Gy,Gx)(8)
其中,各参数的含义如下: G x = [ − 1 0 + 1 − 2 0 + 2 − 1 0 + 1 ] ∗ I , G y = [ + 1 + 2 + 1 0 0 0 − 1 − 2 − 1 ] ∗ I (9) {\bold G}_x= \left[ \begin{matrix} -1 & 0 & +1 \\ -2 & 0 & +2 \\ -1 & 0 & +1\end{matrix} \right]*{\bold I},\ \ {\bold G}_y= \left[ \begin{matrix} +1 & +2 & +1 \\ 0 & 0 & 0 \\ -1 & -2 & -1\end{matrix} \right]*{\bold I}\tag{9} Gx=⎣⎡−1−2−1000+1+2+1⎦⎤∗I, Gy=⎣⎡+10−1+20−2+10−1⎦⎤∗I(9)
这里, Θ \Theta Θ取整为0°、45°、90°或135°,如 [0°, 22.5°] 和 [157.5°, 180°] 映射为0°。
2.3 非极大值抑制
仅仅基于梯度值提取的边缘仍然很模糊,非极大值抑制是一种边缘稀疏技术。具体地,将当前像素的梯度与沿正负梯度方向上的两个像素进行对比,如果当前像素的梯度比另外两个像素的梯度大,则保留该像素点为边缘点;否则将其抑制。如果某点像素 P P P的梯度用红线表示:
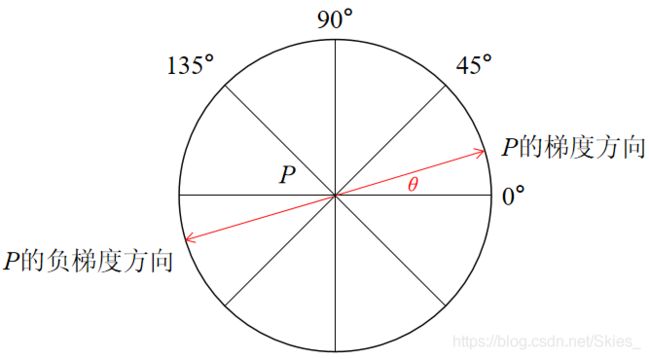
为了简便,在最初的非极大值抑制中,采用量化的方式确定某个像素点的梯度:
- Θ ∈ [ 0 , 22.5 ) ∪ ( − 22.5 , 0 ] ∪ ( 157.5 , 180 ] ∪ ( − 180 , 157.5 ] \Theta\in[0,22.5)\cup(-22.5,0]\cup(157.5,180]\cup(-180,157.5] Θ∈[0,22.5)∪(−22.5,0]∪(157.5,180]∪(−180,157.5],量化为水平方向0°的梯度
- Θ ∈ [ 22.5 , 67.5 ) ∪ ( − 157.5 , − 112.5 ] \Theta\in[22.5,67.5)\cup(-157.5,-112.5] Θ∈[22.5,67.5)∪(−157.5,−112.5],量化为对角线方向45°的梯度
- Θ ∈ [ 67.5 , 112.5 ) ∪ ( − 112.5 , − 67.5 ] \Theta\in[67.5,112.5)\cup(-112.5,-67.5] Θ∈[67.5,112.5)∪(−112.5,−67.5],量化为垂直方向方向90°的梯度
- Θ ∈ [ 112.5 , 157.5 ) ∪ ( − 67.5 , − 22.5 ] \Theta\in[112.5,157.5)\cup(-67.5,-22.5] Θ∈[112.5,157.5)∪(−67.5,−22.5],量化为对角线方向135°的梯度
后来,为了得到更加精确的计算结果,在梯度跨越方向的两个相邻像素之间使用插值的方式来得到待比较像素的梯度。伪代码为:
tan_theta = G_y / G_x
# 正方向梯度
G_1 = (1 - tan_theta) * G_0 + tan_theta * G_45
# 负方向梯度
G_2 = (1 - tan_theta) * G_180 + tan_theta * G_225
2.4 双阈值
为了进一步强化边缘,Canny边缘检测引入双阈值法。具体地,如果该像素值的梯度大于高阈值,则视其为强边缘;如果该像素值介于低阈值与高阈值之间,则视其为弱边缘;否则将其抑制。
2.5 边缘跟踪
基于上一步的结果,对于强边缘的像素点将其视为最后的边缘。其次,如果弱边缘与强边缘有连接,也将其视为最后的边缘;否则将其抑制。这样就得到了最后物体的边缘,即Canny边缘检测整体流程。
基于Canny边缘检测提取多斑点中心:
#include参考
https://github.com/spmallick/learnopencv/tree/master/CenterofBlob