目标检测模型的评价标准-AP与mAP

• 前言
• 一，精确率、召回率与F1
  • 1.1，准确率
  • 1.2，精确率、召回率
  • 1.3，F1 分数
  • 1.4，PR 曲线
    • 1.4.1，如何理解 P-R 曲线
  • 1.5，ROC 曲线与 AUC 面积
• 二，AP 与 mAP
  • 2.1，AP 与 mAP 指标理解
  • 2.2，近似计算AP
  • 2.3，插值计算 AP
  • 2.4，mAP 计算方法
• 三，目标检测度量标准汇总
• 四，参考资料

前言

为了了解模型的泛化能力，即判断模型的好坏，我们需要用某个指标来衡量，有了评价指标，就可以对比不同模型的优劣，并通过这个指标来进一步调参优化模型。对于分类和回归两类监督模型，分别有各自的评判标准。

不同的问题和不同的数据集都会有不同的模型评价指标，比如分类问题，数据集类别平衡的情况下可以使用准确率作为评价指标，但是现实中的数据集几乎都是类别不平衡的，所以一般都是采用 AP 作为分类的评价指标，分别计算每个类别的 AP，再计算mAP。

一，精确率、召回率与F1

1.1，准确率

准确率（精度） – Accuracy，预测正确的结果占总样本的百分比，定义如下：

$$准确率=(TP+TN)/(TP+TN+FP+FN)$$

错误率和精度虽然常用，但是并不能满足所有任务需求。以西瓜问题为例，假设瓜农拉来一车西瓜，我们用训练好的模型对西瓜进行判别，现如精度只能衡量有多少比例的西瓜被我们判断类别正确（两类：好瓜、坏瓜）。但是若我们更加关心的是“挑出的西瓜中有多少比例是好瓜”，或者”所有好瓜中有多少比例被挑出来“，那么精度和错误率这个指标显然是不够用的。

虽然准确率可以判断总的正确率，但是在样本不平衡的情况下，并不能作为很好的指标来衡量结果。举个简单的例子，比如在一个总样本中，正样本占 90%，负样本占 10%，样本是严重不平衡的。对于这种情况，我们只需要将全部样本预测为正样本即可得到 90% 的高准确率，但实际上我们并没有很用心的分类，只是随便无脑一分而已。这就说明了：由于样本不平衡的问题，导致了得到的高准确率结果含有很大的水分。即如果样本不平衡，准确率就会失效。

1.2，精确率、召回率

精确率（查准率）P、召回率（查全率）R 的计算涉及到混淆矩阵的定义，混淆矩阵表格如下：

名称	定义
True Positive(真正例, TP)	将正类预测为正类数
True Negative(真负例, TN)	将负类预测为负类数
False Positive(假正例, FP)	将负类预测为正类数 → 误报 (Type I error)
False Negative(假负例子, FN)	将正类预测为负类数 → 漏报 (Type II error)

查准率与查全率计算公式：

• 查准率（精确率）$P=TP/(TP+FP)$
• 查全率（召回率）$R=TP/(TP+FN)$

精准率和准确率看上去有些类似，但是完全不同的两个概念。精准率代表对正样本结果中的预测准确程度，而准确率则代表整体的预测准确程度，既包括正样本，也包括负样本。

精确率描述了模型有多准，即在预测为正例的结果中，有多少是真正例；召回率则描述了模型有多全，即在为真的样本中，有多少被我们的模型预测为正例。精确率和召回率的区别在于分母不同，一个分母是预测为正的样本数，另一个是原来样本中所有的正样本数。

1.3，F1 分数

如果想要找到 $P$ 和 $R$ 二者之间的一个平衡点，我们就需要一个新的指标：$F1$ 分数。$F1$ 分数同时考虑了查准率和查全率，让二者同时达到最高，取一个平衡。$F1$ 计算公式如下：

这里的 $F1$ 计算是针对二分类模型，多分类任务的 $F1$ 的计算请看下面。

$$F1=\frac{2\times P\times R}{P+R}=\frac{2\times TP}{样例总数+TP-TN}$$

$F1$ 度量的一般形式：$F_{\beta }$，能让我们表达出对查准率/查全率的偏见，$F_{\beta }$ 计算公式如下：

$$F_{\beta }=\frac{1+{\beta }^2\times P\times R}{({\beta }^2\times P)+R}$$

其中 $\beta >1$ 对查全率有更大影响，$\beta <1$ 对查准率有更大影响。

不同的计算机视觉问题，对两类错误有不同的偏好，常常在某一类错误不多于一定阈值的情况下，努力减少另一类错误。在目标检测中，mAP（mean Average Precision）作为一个统一的指标将这两种错误兼顾考虑。

很多时候我们会有多个混淆矩阵，例如进行多次训练/测试，每次都能得到一个混淆矩阵；或者是在多个数据集上进行训练/测试，希望估计算法的”全局“性能；又或者是执行多分类任务，每两两类别的组合都对应一个混淆矩阵；…总而来说，我们希望能在 $n$ 个二分类混淆矩阵上综合考虑查准率和查全率。

一种直接的做法是先在各混淆矩阵上分别计算出查准率和查全率，记为$(P_1,R_1),(P_2,R_2),...,(P_n,R_n)$ 然后取平均，这样得到的是”宏查准率（Macro-P）“、”宏查准率（Macro-R）“及对应的”宏$F1$（Macro-F1）“：
$$MacroP=\frac{1}{n}\sum _{i=1}^n{P}_i$$
$$MacroR=\frac{1}{n}\sum _{i=1}^n{R}_i$$
$$MacroF1=\frac{2\times MacroP\times MacroR}{MacroP+MacroR}$$

另一种做法是将各混淆矩阵对应元素进行平均，得到 $TP、FP、TN、FN$ 的平均值，再基于这些平均值计算出”微查准率“（Micro-P）、”微查全率“（Micro-R）和”微$F1$“（Mairo-F1）

$$MicroP=\frac{\overline{TP}}{\overline{TP}+\overline{FP}}$$
$$MicroR=\frac{\overline{TP}}{\overline{TP}+\overline{FN}}$$
$$MicroF1=\frac{2\times MicroP\times MicroR}{MacroP+MicroR}$$

1.4，PR 曲线

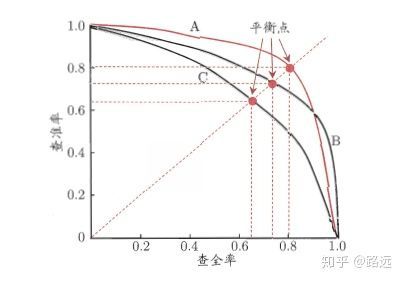
精准率和召回率的关系可以用一个 P-R 图来展示，以查准率 P 为纵轴、查全率 R 为横轴作图，就得到了查准率－查全率曲线，简称 P-R 曲线，PR 曲线下的面积定义为 AP:

1.4.1，如何理解 P-R 曲线

可以从排序型模型或者分类模型理解。以逻辑回归举例，逻辑回归的输出是一个 0 到 1 之间的概率数字，因此，如果我们想要根据这个概率判断用户好坏的话，我们就必须定义一个阈值 。通常来讲，逻辑回归的概率越大说明越接近 1，也就可以说他是坏用户的可能性更大。比如，我们定义了阈值为 0.5，即概率小于 0.5 的我们都认为是好用户，而大于 0.5 都认为是坏用户。因此，对于阈值为 0.5 的情况下，我们可以得到相应的一对查准率和查全率。

但问题是：这个阈值是我们随便定义的，我们并不知道这个阈值是否符合我们的要求。 因此，为了找到一个最合适的阈值满足我们的要求，我们就必须遍历 0 到 1 之间所有的阈值，而每个阈值下都对应着一对查准率和查全率，从而我们就得到了 PR 曲线。

最后如何找到最好的阈值点呢？ 首先，需要说明的是我们对于这两个指标的要求：我们希望查准率和查全率同时都非常高。 但实际上这两个指标是一对矛盾体，无法做到双高。图中明显看到，如果其中一个非常高，另一个肯定会非常低。选取合适的阈值点要根据实际需求，比如我们想要高的查全率，那么我们就会牺牲一些查准率，在保证查全率最高的情况下，查准率也不那么低。。

1.5，ROC 曲线与 AUC 面积

• PR 曲线是以 Recall 为横轴，Precision 为纵轴；而 ROC 曲线则是以 FPR 为横轴，TPR 为纵轴**。P-R 曲线越靠近右上角性能越好。PR 曲线的两个指标都聚焦于正例
• PR 曲线展示的是 Precision vs Recall 的曲线，ROC 曲线展示的是 FPR（x 轴：False positive rate） vs TPR（True positive rate, TPR）曲线。

1. ROC 曲线
2. AUC 面积

二，AP 与 mAP

2.1，AP 与 mAP 指标理解

AP 衡量的是训练好的模型在每个类别上的好坏，mAP 衡量的是模型在所有类别上的好坏，得到 AP 后 mAP 的计算就变得很简单了，就是取所有 AP 的平均值。AP 的计算公式比较复杂（所以单独作一章节内容），详细内容参考下文。

mAP 这个术语有不同的定义。此度量指标通常用于信息检索、图像分类和目标检测领域。然而这两个领域计算 mAP 的方式却不相同。这里我们只谈论目标检测中的 mAP 计算方法。

mAP 常作为目标检测算法的评价指标，具体来说就是，对于每张图片检测模型会输出多个预测框（远超真实框的个数），我们使用 IoU (Intersection Over Union，交并比)来标记预测框是否预测准确。标记完成后，随着预测框的增多，查全率 R 总会上升，在不同查全率 R 水平下对准确率 P 做平均，即得到 AP，最后再对所有类别按其所占比例做平均，即得到 mAP 指标。

2.2，近似计算AP

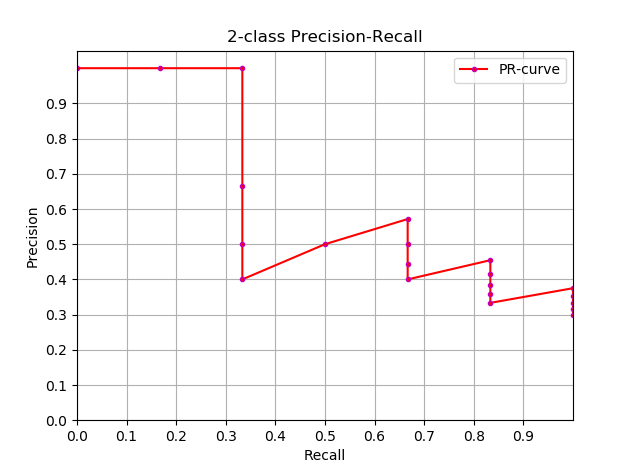
知道了AP 的定义，下一步就是理解AP计算的实现，理论上可以通过积分来计算AP，公式如下：
$$AP={\int }_0^{1}P(r)dr$$
但通常情况下都是使用近似或者插值的方法来计算 $AP$。

$$AP=\sum _{k=1}^{N}P(k)\Delta r(k)$$

• 近似计算 $AP$ (approximated average precision)，这种计算方式是 approximated 形式的；
• 很显然位于一条竖直线上的点对计算 $AP$ 没有贡献；
• 这里 $N$ 为数据总量，$k$ 为每个样本点的索引， $\Delta r(k)=r(k)-r(k-1)$。

近似计算 AP 和绘制 PR 曲线代码如下：

import numpy as np
import matplotlib.pyplot as plt

class_names = ["car", "pedestrians", "bicycle"]

def draw_PR_curve(predict_scores, eval_labels, name, cls_idx=1):
    """calculate AP and draw PR curve, there are 3 types
    Parameters:
    @all_scores: single test dataset predict scores array, (-1, 3)
    @all_labels: single test dataset predict label array, (-1, 3)
    @cls_idx: the serial number of the AP to be calculated, example: 0,1,2,3...
    """
    # print('sklearn Macro-F1-Score:', f1_score(predict_scores, eval_labels, average='macro'))
    global class_names
    fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(15, 10))
    # Rank the predicted scores from large to small, extract their corresponding index(index number), and generate an array
    idx = predict_scores[:, cls_idx].argsort()[::-1]
    eval_labels_descend = eval_labels[idx]
    pos_gt_num = np.sum(eval_labels == cls_idx) # number of all gt

    predict_results = np.ones_like(eval_labels)
    tp_arr = np.logical_and(predict_results == cls_idx, eval_labels_descend == cls_idx) # ndarray
    fp_arr = np.logical_and(predict_results == cls_idx, eval_labels_descend != cls_idx)

    tp_cum = np.cumsum(tp_arr).astype(float) # ndarray, Cumulative sum of array elements.
    fp_cum = np.cumsum(fp_arr).astype(float)

    precision_arr = tp_cum / (tp_cum + fp_cum) # ndarray
    recall_arr = tp_cum / pos_gt_num
    ap = 0.0
    prev_recall = 0
    for p, r in zip(precision_arr, recall_arr):
      ap += p * (r - prev_recall)
      # pdb.set_trace()
      prev_recall = r
    print("------%s, ap: %f-----" % (name, ap))

    fig_label = '[%s, %s] ap=%f' % (name, class_names[cls_idx], ap)
    ax.plot(recall_arr, precision_arr, label=fig_label)

    ax.legend(loc="lower left")
    ax.set_title("PR curve about class: %s" % (class_names[cls_idx]))
    ax.set(xticks=np.arange(0., 1, 0.05), yticks=np.arange(0., 1, 0.05))
    ax.set(xlabel="recall", ylabel="precision", xlim=[0, 1], ylim=[0, 1])

    fig.savefig("./pr-curve-%s.png" % class_names[cls_idx])
    plt.close(fig)

2.3，插值计算 AP

插值计算(Interpolated average precision) $AP$ 的公式的演变过程这里不做讨论，详情可以参考这篇文章，我这里的公式和图也是参考此文章的。11 点插值计算方式计算 $AP$ 公式如下：

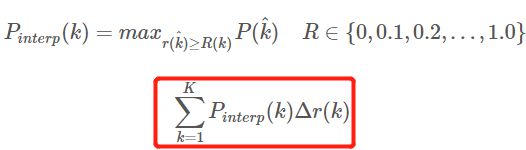
• 这是通常意义上的 11 points_Interpolated 形式的 AP，选取固定的 $0,0.1,0.2,\dots ,1.0$ 11 个阈值，这个在 PASCAL2007 中使用
• 这里因为参与计算的只有 11 个点，所以 $K=11$，称为 11 points_Interpolated，$k$ 为阈值索引
• $P_{interp}(k)$ 取第 $k$ 个阈值所对应的样本点之后的样本中的最大值，只不过这里的阈值被限定在了 $0,0.1,0.2,\dots ,1.0$ 范围内。
  

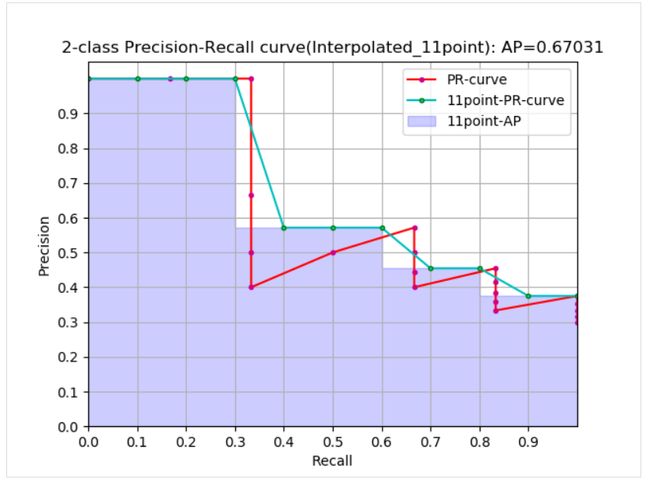
从曲线上看，真实 AP< approximated AP < Interpolated AP，11-points Interpolated AP 可能大也可能小，当数据量很多的时候会接近于 Interpolated AP，与 Interpolated AP 不同，前面的公式中计算 AP 时都是对 PR 曲线的面积估计，PASCAL 的论文里给出的公式就更加简单粗暴了，直接计算11 个阈值处的 precision 的平均值。PASCAL 论文给出的 11 点计算 AP 的公式如下。

1, 在给定 recal 和 precision 的条件下计算 AP：

def voc_ap(rec, prec, use_07_metric=False):
    """ 
    ap = voc_ap(rec, prec, [use_07_metric])
    Compute VOC AP given precision and recall.
    If use_07_metric is true, uses the
    VOC 07 11 point method (default:False).
    """
    if use_07_metric:
        # 11 point metric
        ap = 0.
        for t in np.arange(0., 1.1, 0.1):
            if np.sum(rec >= t) == 0:
                p = 0
            else:
                p = np.max(prec[rec >= t])
            ap = ap + p / 11.
    else:
        # correct AP calculation
        # first append sentinel values at the end
        mrec = np.concatenate(([0.], rec, [1.]))
        mpre = np.concatenate(([0.], prec, [0.]))

        # compute the precision envelope
        for i in range(mpre.size - 1, 0, -1):
            mpre[i - 1] = np.maximum(mpre[i - 1], mpre[i])

        # to calculate area under PR curve, look for points
        # where X axis (recall) changes value
        i = np.where(mrec[1:] != mrec[:-1])[0]

        # and sum (\Delta recall) * prec
        ap = np.sum((mrec[i + 1] - mrec[i]) * mpre[i + 1])
    return ap

2，给定目标检测结果文件和测试集标签文件 xml 等计算 AP：

def parse_rec(filename):
    """ Parse a PASCAL VOC xml file 
    Return : list, element is dict.
    """
    tree = ET.parse(filename)
    objects = []
    for obj in tree.findall('object'):
        obj_struct = {}
        obj_struct['name'] = obj.find('name').text
        obj_struct['pose'] = obj.find('pose').text
        obj_struct['truncated'] = int(obj.find('truncated').text)
        obj_struct['difficult'] = int(obj.find('difficult').text)
        bbox = obj.find('bndbox')
        obj_struct['bbox'] = [int(bbox.find('xmin').text),
                              int(bbox.find('ymin').text),
                              int(bbox.find('xmax').text),
                              int(bbox.find('ymax').text)]
        objects.append(obj_struct)

    return objects

def voc_eval(detpath,
             annopath,
             imagesetfile,
             classname,
             cachedir,
             ovthresh=0.5,
             use_07_metric=False):
    """rec, prec, ap = voc_eval(detpath,
                                annopath,
                                imagesetfile,
                                classname,
                                [ovthresh],
                                [use_07_metric])
    Top level function that does the PASCAL VOC evaluation.
    detpath: Path to detections result file
        detpath.format(classname) should produce the detection results file.
    annopath: Path to annotations file
        annopath.format(imagename) should be the xml annotations file.
    imagesetfile: Text file containing the list of images, one image per line.
    classname: Category name (duh)
    cachedir: Directory for caching the annotations
    [ovthresh]: Overlap threshold (default = 0.5)
    [use_07_metric]: Whether to use VOC07's 11 point AP computation
        (default False)
    """
    # assumes detections are in detpath.format(classname)
    # assumes annotations are in annopath.format(imagename)
    # assumes imagesetfile is a text file with each line an image name
    # cachedir caches the annotations in a pickle file

    # first load gt
    if not os.path.isdir(cachedir):
        os.mkdir(cachedir)
    cachefile = os.path.join(cachedir, '%s_annots.pkl' % imagesetfile)
    # read list of images
    with open(imagesetfile, 'r') as f:
        lines = f.readlines()
    imagenames = [x.strip() for x in lines]

    if not os.path.isfile(cachefile):
        # load annotations
        recs = {}
        for i, imagename in enumerate(imagenames):
            recs[imagename] = parse_rec(annopath.format(imagename))
            if i % 100 == 0:
                print('Reading annotation for {:d}/{:d}'.format(
                    i + 1, len(imagenames)))
        # save
        print('Saving cached annotations to {:s}'.format(cachefile))
        with open(cachefile, 'wb') as f:
            pickle.dump(recs, f)
    else:
        # load
        with open(cachefile, 'rb') as f:
            try:
                recs = pickle.load(f)
            except:
                recs = pickle.load(f, encoding='bytes')

    # extract gt objects for this class
    class_recs = {}
    npos = 0
    for imagename in imagenames:
        R = [obj for obj in recs[imagename] if obj['name'] == classname]
        bbox = np.array([x['bbox'] for x in R])
        difficult = np.array([x['difficult'] for x in R]).astype(np.bool)
        det = [False] * len(R)
        npos = npos + sum(~difficult)
        class_recs[imagename] = {'bbox': bbox,
                                 'difficult': difficult,
                                 'det': det}

    # read dets
    detfile = detpath.format(classname)
    with open(detfile, 'r') as f:
        lines = f.readlines()

    splitlines = [x.strip().split(' ') for x in lines]
    image_ids = [x[0] for x in splitlines]
    confidence = np.array([float(x[1]) for x in splitlines])
    BB = np.array([[float(z) for z in x[2:]] for x in splitlines])

    nd = len(image_ids)
    tp = np.zeros(nd)
    fp = np.zeros(nd)

    if BB.shape[0] > 0:
        # sort by confidence
        sorted_ind = np.argsort(-confidence)
        sorted_scores = np.sort(-confidence)
        BB = BB[sorted_ind, :]
        image_ids = [image_ids[x] for x in sorted_ind]

        # go down dets and mark TPs and FPs
        for d in range(nd):
            R = class_recs[image_ids[d]]
            bb = BB[d, :].astype(float)
            ovmax = -np.inf
            BBGT = R['bbox'].astype(float)

            if BBGT.size > 0:
                # compute overlaps
                # intersection
                ixmin = np.maximum(BBGT[:, 0], bb[0])
                iymin = np.maximum(BBGT[:, 1], bb[1])
                ixmax = np.minimum(BBGT[:, 2], bb[2])
                iymax = np.minimum(BBGT[:, 3], bb[3])
                iw = np.maximum(ixmax - ixmin + 1., 0.)
                ih = np.maximum(iymax - iymin + 1., 0.)
                inters = iw * ih

                # union
                uni = ((bb[2] - bb[0] + 1.) * (bb[3] - bb[1] + 1.) +
                       (BBGT[:, 2] - BBGT[:, 0] + 1.) *
                       (BBGT[:, 3] - BBGT[:, 1] + 1.) - inters)

                overlaps = inters / uni
                ovmax = np.max(overlaps)
                jmax = np.argmax(overlaps)

            if ovmax > ovthresh:
                if not R['difficult'][jmax]:
                    if not R['det'][jmax]:
                        tp[d] = 1.
                        R['det'][jmax] = 1
                    else:
                        fp[d] = 1.
            else:
                fp[d] = 1.

    # compute precision recall
    fp = np.cumsum(fp)
    tp = np.cumsum(tp)
    rec = tp / float(npos)
    # avoid divide by zero in case the first detection matches a difficult
    # ground truth
    prec = tp / np.maximum(tp + fp, np.finfo(np.float64).eps)
    ap = voc_ap(rec, prec, use_07_metric)

    return rec, prec, ap

2.4，mAP 计算方法

因为 $mAP$ 值的计算是对数据集中所有类别的 $AP$ 值求平均，所以我们要计算 $mAP$，首先得知道某一类别的 $AP$ 值怎么求。不同数据集的某类别的 $AP$ 计算方法大同小异，主要分为三种：

（1）在 VOC2007，只需要选取当 $Recall>=0,0.1,0.2,...,1$ 共 11 个点时的 Precision 最大值，然后 $AP$ 就是这 11 个 Precision 的平均值，$mAP$ 就是所有类别 $AP$ 值的平均。VOC 数据集中计算 $AP$ 的代码（用的是插值计算方法，代码出自py-faster-rcnn仓库）

（2）在 VOC2010 及以后，需要针对每一个不同的 Recall 值（包括 0 和 1），选取其大于等于这些 Recall 值时的 Precision 最大值，然后计算 PR 曲线下面积作为 $AP$ 值，$mAP$ 就是所有类别 $AP$ 值的平均。

（3）COCO 数据集，设定多个 IOU 阈值（0.5-0.95, 0.05 为步长），在每一个 IOU 阈值下都有某一类别的 AP 值，然后求不同 IOU 阈值下的 AP 平均，就是所求的最终的某类别的 AP 值。

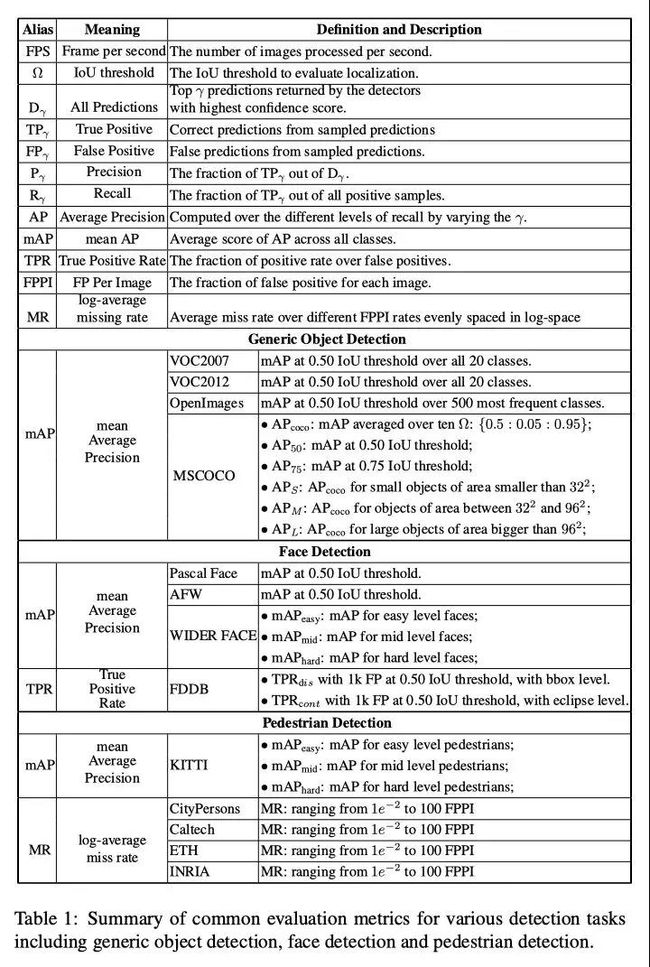
三，目标检测度量标准汇总

评价指标	定义及理解
mAP	mean Average Precision, 即各类别 AP 的平均值
AP	PR 曲线下面积，后文会详细讲解
PR 曲线	Precision-Recall 曲线
Precision	$TP/(TP+FP)$
Recall	$TP/(TP+FN)$
TP	IoU>0.5 的检测框数量（同一 Ground Truth 只计算一次，阈值取 0.5）
FP	IoU<=0.5 的检测框，或者是检测到同一个 GT 的多余检测框的数量
FN	没有检测到的 GT 的数量

四，参考资料

• 目标检测评价标准-AP mAP
• 目标检测的性能评价指标
• Soft-NMS
• Recent Advances in Deep Learning for Object Detection
• A Simple and Fast Implementation of Faster R-CNN
• 分类模型评估指标——准确率、精准率、召回率、F1、ROC曲线、AUC曲线
• 一文让你彻底理解准确率，精准率，召回率，真正率，假正率，ROC/AUC