基于MWORKS.Syslab的机器学习算法应用案例-动物咳嗽检测

1 背景介绍

咳嗽是呼吸道疾病的一种很常见的临床症状。咳嗽声中包含喉部、气管或肺等受刺激时的振动信息，通过对此类振动信息的研究可以对动物的患病状况做出提前预警。在大规模的动物养殖过程中，通过咳嗽信息提前对患病动物进行干预治疗能够有效的减少动物的死亡率。

在实际工程中，首先通过仿真平台进行算法的设计与验证，再将算法应用到实际设备上，能够极大地节约人力物力。MWORKS.Syslab是同元软控全新推出的新一代科学计算软件，能够支持信号处理、通信、机器学习及等多领域的算法设计与分析，同时提供功能强大的可视化分析工具。下面基于MWORKS.Syslab设计动物咳嗽检测算法并分析算法性能。

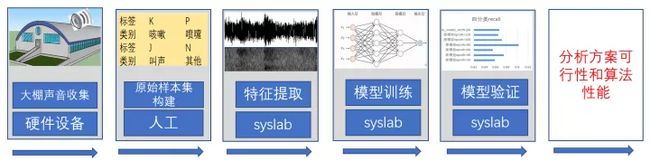
△ 动物咳嗽检测算法设计流程

2 声音采集及样本集构建

首先需要对动物养殖大棚中的各种声音进行收集，这里选取猪只养殖大棚，实际环境中存在的较为常见的声音为叫声、喷嚏、咳嗽、噪声等。选取采样频率为16KHz，每段音频长度截取成0.8s，采集需要的音频数据，并构建所需要的样本集。音频数据处理后以.h5文件的形式存储，x字段存储音频数据，y字段存储对应标签。

下表为标签同各种音频的对应关系：

选用的样本集里只保留干咳、喷嚏、叫声、噪声四种音频。基于MWORKS.Syslab，对叫声、喷嚏、咳嗽、噪声等音频信号进行时频域分析，对应代码如下：

# Julia Code
x = h5read("dataset.h5", "/x")  # 采集到的音频数据集
x_K = x[:, 5]   # 某段咳嗽音频
x_P = x[:,49]  # 某段喷嚏音频
x_J = x[:,9]   # 某段叫声音频
x_N = x[:,32]   # 某段噪声音频
fs=16e3;T=0.8
t=0:1/fs:(T-1/fs)
f=-fs/2:1/T:(fs/2-1/T)
figure("时域音频信号")  #绘制时域音频信号
subplot(2, 2, 1);plot(t,x_K);title("咳嗽");xlabel("时间/s");ylabel("幅度");
subplot(2, 2, 2);plot(t,x_P);title("喷嚏");xlabel("时间/s");ylabel("幅度");
subplot(2, 2, 3);plot(t,x_J);title("叫声");xlabel("时间/s");ylabel("幅度");
subplot(2, 2, 4);plot(t,x_N);title("噪声");xlabel("时间/s");ylabel("幅度");
tightlayout()
figure("频域音频信号")  #绘制频域音频信号
subplot(2, 2, 1);plot(f,fftshift(fft(x_K)));title("咳嗽");xlabel("频率/Hz");ylabel("幅度");ylim([-10,10])
subplot(2, 2, 2);plot(f,fftshift(fft(x_P)));title("喷嚏");xlabel("频率/Hz");ylabel("幅度");ylim([-10,10])
subplot(2, 2, 3);plot(f,fftshift(fft(x_J)));title("叫声");xlabel("频率/Hz");ylabel("幅度");ylim([-10,10])
subplot(2, 2, 4);plot(f,fftshift(fft(x_N)));title("噪声");xlabel("频率/Hz");ylabel("幅度");ylim([-10,10])
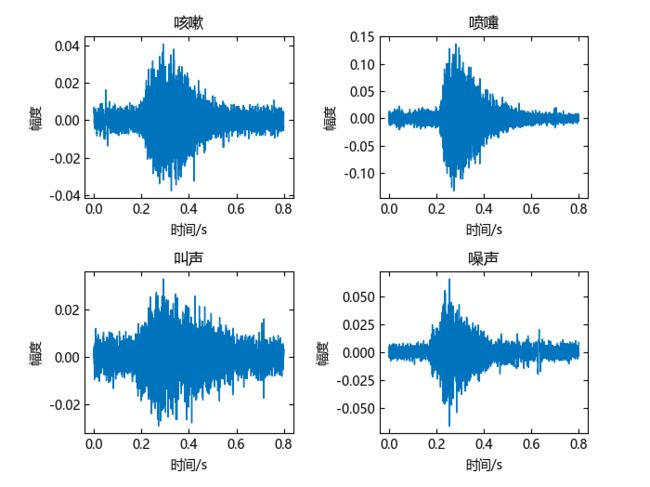
tightlayout()

四种音频信号的时域和频域形式如下：

△ 时域音频信号

△ 频域音频信号

3 特征提取

3.1 声谱图

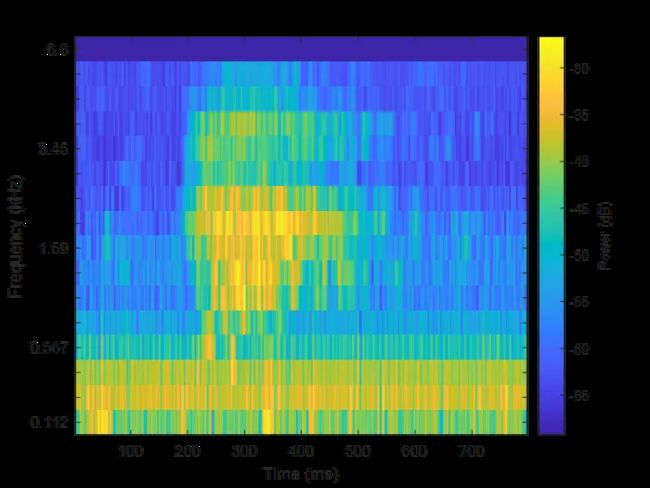
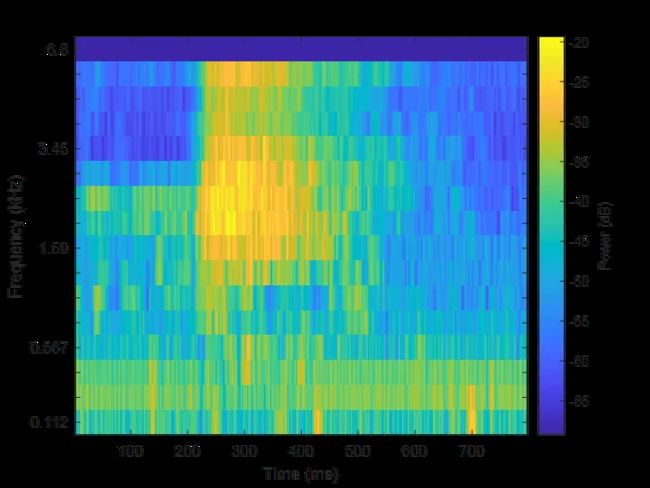
标准的傅里叶变换适用于周期、瞬变或平稳随机信号，而现实中的咳嗽信号是一个非平稳的过程，所以直接通过傅里叶变换并不能很好表现出信号的频域特征。短时傅里叶变换则是首先选取一个固定的窗函数，把整个时域过程分解成无数个等长的小过程，每个小过程近似平稳，然后分别对每个小过程机进行傅里叶变换，音频信号短时傅里叶变换后的结果也称声谱图，声谱图能够有效的表示音频信号频域特征。窗函数选取汉明窗，窗长度选取128，窗口重叠长度选择96，傅里叶变换长度同窗长度相同，绘制音频信号的声谱图及代码如下：

△ 咳嗽

△ 喷嚏

△ 叫声

△ 噪声

# Julia Code

figure("stft咳嗽")
s1, f1, t1 = stft(x_K; Window=hann(128, "periodic"); OverlapLength=96; plotfig=true)
figure("stft喷嚏")
s2, f2, t2 = stft(x_P; Window=hann(128, "periodic"); OverlapLength=96;plotfig=true)
figure("stft叫声")
s3, f3, t3 = stft(x_J; Window=hann(128, "periodic"); OverlapLength=96; plotfig=true)
figure("stft噪声")
s4, f4, t4 = stft(x_N; Window=hann(128, "periodic"); OverlapLength=96; plotfig=true)

3.2 梅尔谱

人耳的可听频率范围为20Hz~20kHz，并且对低频信号的感知要比高频信号敏感。例如，人们可以比较容易地发现500和1000Hz的区别，却很难发现7500和8000Hz的区别。梅尔标度是Hz的非线性变换，对于以梅尔标度为单位的信号，可以做到人们对于相同频率差别的信号的感知能力几乎相同。一个常用的变换公式为：

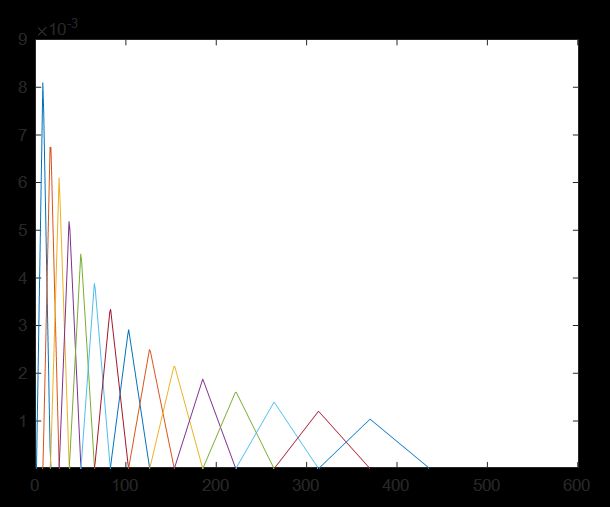
梅尔谱就是一个在梅尔标度下的声谱，是通过原始声谱与若干个梅尔滤波器点乘得到。下图为采样频率为16000Hz，滤波器长度为1024，滤波器个数为16时设计出来的梅尔滤波器组图及代码实现：

△ 梅尔滤波器组

# Julia Code
filterBank, F, FFTLengthTooSmall = designMelFilterBank(16000, 16, 1024)
plot(filterBank)

由于梅尔谱相当于是把很宽的频率范围给缩小到了人类可以正常感知的范围，而且很大程度上保留了人耳理解原本语音所需的信息。下图为选取梅尔滤波器组个数为64，采样频率为16000Hz时，不同音频信号的梅尔谱及代码实现：

△ 咳嗽

△ 喷嚏

△ 叫声

△ 噪声

# Julia Code

x = h5read("dataset.h5", "/x");
x_K = x[:, 5];
x_P = x[:, 49];
x_J = x[:, 9];
x_N = x[:, 3];
s1, f1, t1 = melSpectrogram(x_K, 16000; WindowLength=128, OverlapLength=96, NumBands=64, FFTLength=256,plotfig=true)
s2, f2, t2 = melSpectrogram(x_P, 16000; WindowLength=128, OverlapLength=96, NumBands=64, FFTLength=256,plotfig=true)
s3, f3, t3 = melSpectrogram(x_J, 16000; WindowLength=128, OverlapLength=96, NumBands=64, FFTLength=256,plotfig=true)
s4, f4, t4 = melSpectrogram(x_N, 16000; WindowLength=128, OverlapLength=96, NumBands=64, FFTLength=256,plotfig=true)

4 模型训练

识别算法是进行咳嗽声识别的核心，识别算法的性能直接决定了识别效果的好坏。识别过程即在设计好模型基础上，将所提取目标特征作为系统训练和测试数据集，通过机器学习的方法，使算法对训练数据集进行学习，并从中找出所学目标的特征差异，进一步学习到收敛的识别模型，最后借助此模型对测试数据集进行测试来评估算法性能。这里选用人工神经网络模型来完成识别。

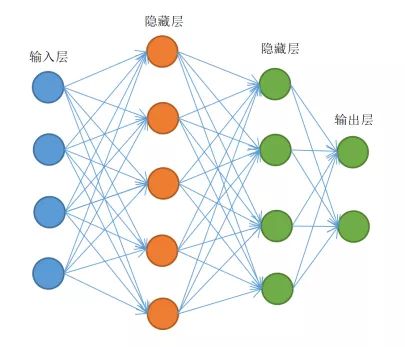
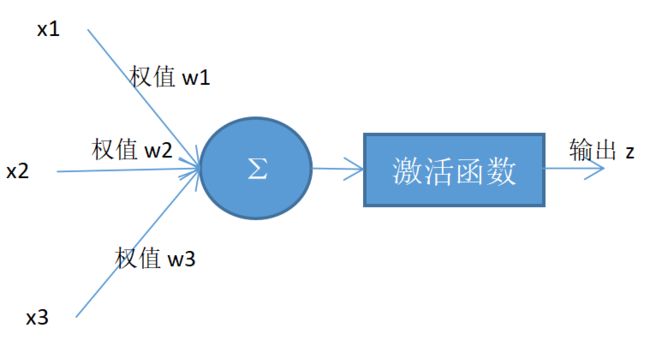
人工神经网络由节点层组成，包含一个输入层、一个或多个隐藏层和一个输出层。 每个节点也称为一个人工神经元，它们连接到另一个节点，具有相关的权重和阈值。 如果任何单个节点的输出高于指定的阈值，那么该节点将被激活，并将数据发送到网络的下一层；否则，不会将数据传递到网络的下一层。下图为简单的神经网络模型和单个节点模型：

△ 神经网络模型

△ 单个节点模型

可以通过以下代码构建一个神经网络模型，featuresiz为输入的特征维度，也即输入层的节点个数；relu、softmax为激活函数；ps存储初始权值。

# Julia Code
using Flux
model = Flux.Chain(
    Dense(featuresiz, 1024, relu), 
    Dense(1024, 64, relu),
Dense(64, 8),softmax)
ps = Flux.params(model)

神经网络的训练过程可以看作为一个优化问题，最小化目标函数 J(θ) ，最优化的求解过程，首先求解目标函数的梯度 ▽J(θ) ，然后将参数 θ 向负梯度方向更新， θt=θt−1−η▽J(θ) ， η 为学习率，表明梯度更新的步伐大小，学习率决定目标函数能否收敛到局部最小值以及何时收敛到最小值。合适的学习率能够使目标函数在合适的时间内收敛到局部最小值。最优化的过程依赖的算法称为优化器。选择初始学习率为0.01，优化器为adam优化器，该优化器的学习率能随梯度自适应的改变。

# Julia Code
learn_rate = 0.01
opt = ADAM(learn_rate)

每个批次的训练数据送入模型后，通过前向传播输出预测值，然后会通过损失函数计算出预测值和真实值之间的差异值，称为损失值。得到损失值之后，模型通过反向传播去更新各个参数，来降低真实值与预测值之间的损失，使得模型生成的预测值往真实值方向靠拢，从而达到学习的目的。这里选用较为常用的交叉熵作为损失函数：

# Julia Code
loss(x, y) = crossentropy(model(x), y)

利用训练集提取出来的特征数据（声谱或梅尔谱）来对原始模型进行训练，通过迭代不断优化模型的参数值，使得损失函数越来越小。选取合适的迭代次数，保存对应的模型。附代码如下：

# Julia Code
x_raw = h5read("dataset.h5", "/x")
y_raw = h5read("dataset.h5", "/y")
x_train_raw = x_raw[1600:end-1600, 1:5000]  #前5000个作为训练集
y_train_raw = y_raw[1:5000]
WindowLen = 512
X_train = zeros(WindowLen * 36,   size(x_train_raw, 2))
for i = 1:size(X_train, 2)
    X_train[:, i] = vec((abs.(stft(x_train_raw[:, i], fs;   Window=kaiser(WindowLen, 5), OverlapLength=256)[1])))
end
X_train = X_train / maximum(abs.(X_train))  #归一化
Y_train = onehotbatch(y_train_raw, 0:7)
 
loss_history = Float64[]
epochs = 120
for epoch = 1:epochs
    Flux.train!(loss, ps, [(X_train, Y_train)], opt)
    train_loss = loss(X_train, Y_train)
    push!(loss_history, train_loss)
    println("Epoch= $epoch : Train loss = $train_loss")
    if mod(epoch, 10) == 0
        @save "model$epoch.bson" model
    end
end
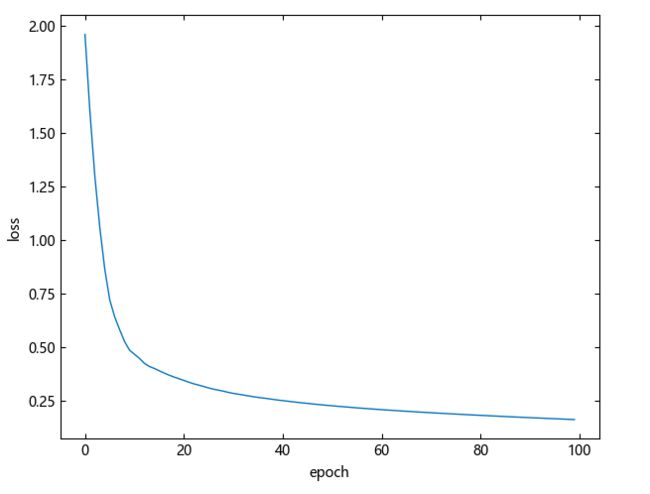
plot(loss_history)
xlabel("epoch")
ylabel("loss")

△ 损失函数曲线

5 模型验证

动物咳嗽检测问题，实际就是一个分类问题，需要通过模型把咳嗽、喷嚏、叫声、噪声这几种声音分开。对于模型的验证及评价可以通过准确率和召回率来评判，准确率（accuracy）定义为分类正确的样本数占总样本数的比例；召回率（recall）定义为正样本数被预测正确的比例。选用样本集的后5000个作为测试集，用声谱图或者梅尔谱作为特征训练得到模型，并利用测试集计算准确率和召回率，附代码如下：

# Julia Code
x_test_raw = x_raw[1600:end-1600, end-4999:end]
y_test = y_raw[end-4999:end]
X_test = zeros(WindowLen * 36, size(x_test_raw, 2))
for i = 1:size(x_test_raw, 2)
    X_test[:, i] = vec((abs.(stft(x_test_raw[:, i], fs; Window=kaiser(WindowLen, 5), OverlapLength=256)[1])))
end
X_test = X_test / maximum(abs.(X_test))
y_hat = onecold(model(X_test), 0:7)
 
#四分类
acc4 = length(find(y_hat - y_test .== 0)) / length(y_test)
recall4 = length(find(y_hat[find(y_test .== 0)] .== 0)) / length(find(y_test .== 0))
#二分类
acc2 = (length(find(y_hat[find(y_test .== 0)] .== 0)) + length(find(y_hat[find(y_test .!= 0)] .!= 0))) / length(y_test)
recall2 = length(find(y_hat[find(y_test .== 0)] .== 0)) / length(find(y_test .== 0))

下面分别为采用声谱和梅尔谱作为特征，在迭代不同次数时得到四分类和二分类的准确率和召回率，其中二分类指将喷嚏、叫声、噪声统一归为其他，即只存在其他和咳嗽两种样本。下面为对应准确率和召回率：

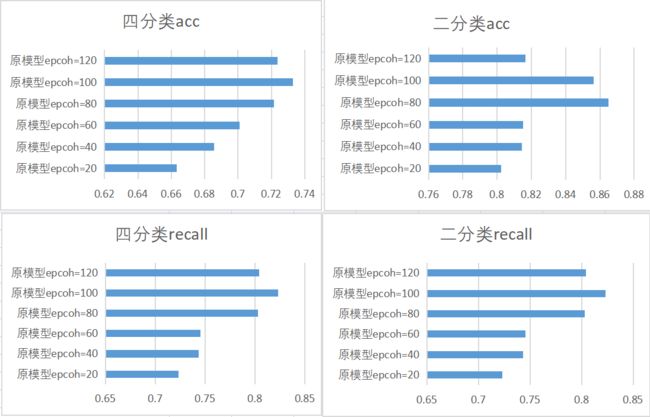
△ 采用声谱图作为特征

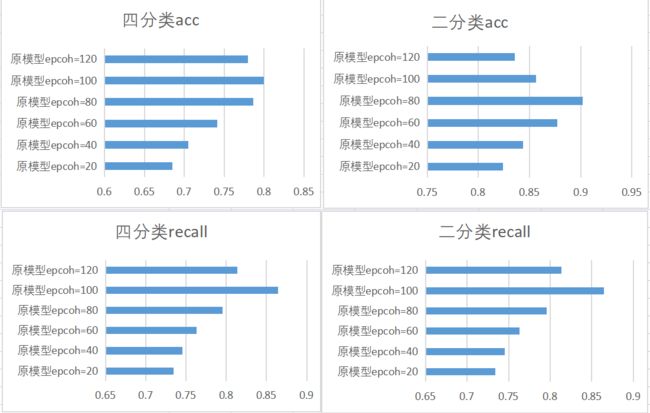
△ 采用梅尔谱作为特征

采用声谱图作为特征来进行动物的咳嗽识别的模型简称为模型1，采用梅尔谱作为特征的模型简称为模型2。

由上述仿真结果可知，在四分类情况下，epoch=100时能够得到较好的准确率和召回率，且模型2的效果要好于模型1。在二分类情况下，准确率和召回率达到最大时的epoch值不同，但总体来看模型2的效果优于模型1。所以在对比分析后，可以选取模型2在epoch=100时得到的模型来进行咳嗽识别。

6 识别结果

下面对选定的模型效果进行详细测试，选择7组测试集，里面咳嗽、喷嚏、叫声、噪声的样本数量均为1000，分别将这几种音频数据输入到选定模型，记录模型在二分类情况下识别的准确率。由结果可知，选定模型能够正确识别咳嗽概率接近90%，说明模型对咳嗽的识别效果良好，当然还可以通过一些其他方法来增加识别的准确率，如采用其他的特征、更换更为复杂的模型等。

△ 选定模型识别咳嗽准确率

通过MWORKS.Syslab设计的算法模型可保存为bson文件，选择合适的模型将其部署到云端并同对应的音频收集设备建立连接，既可以对动物的咳嗽声音进行识别，并通过计算咳嗽次数来对动物的是否存在呼吸道疾病进行相应预警。

7 总结

本文基于MWORKS.Syslab设计了动物咳嗽检测算法，并采用了声谱图和梅尔谱作为特征训练神经网络模型，分析了两种情况下训练的模型对动物咳嗽检测的效果，筛选出较适合的识别模型，能够支持实际应用。

除上文算法相关内容外，MWORKS.Syslab集成了信号、通信、机器学习等相关领域常见的基础算法，能够支持多领域的算法设计与分析，帮助工程人员快速设计和分析算法，支撑实际工程应用。

MWORKS.Syslab 的基础版供用户免费使用，欢迎大家前往同元软控官网下载。