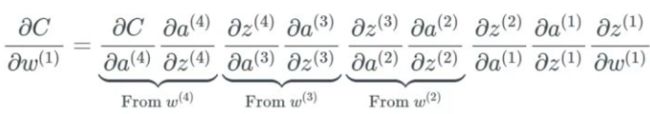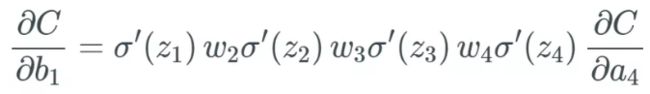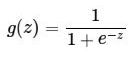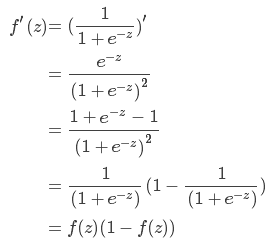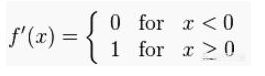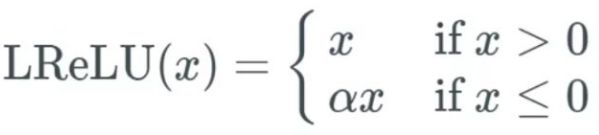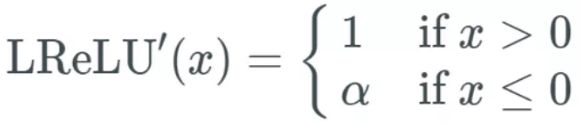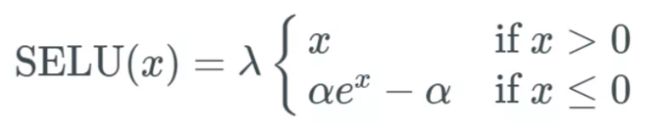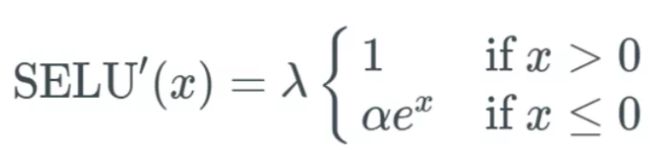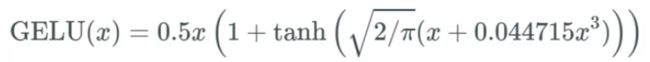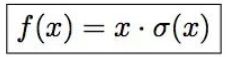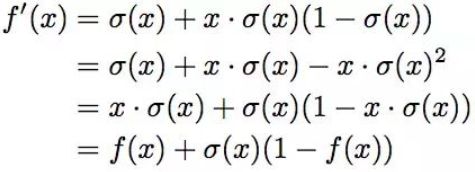从sigmoid到GELU——神经网络中的激活函数

       

目录

一、激活函数及其作用

二、激活函数的分类

1、sigmoid

2、tanh激活函数

3、RELU函数——Rectified Linear Unit——整流线性单元

4、Leaky ReLU

5、SELU

6、GELU

7、swish

---

         作为深度学习神经网络中非常重要的一个部分，弄清楚激活函数，对我们夯实基础起很重要的作用，下面就一一来学习一下激活函数。

一、激活函数及其作用

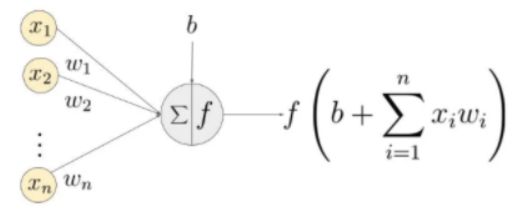
        什么是激活函数呢？其实激活函数并不是很难理解的一个概念。这里激活函数就可以看做一个函数一个映射，对于单个神经元来说，激活函数的功能就是起一个限制阀的作用——控制输入——不让它进入神经网络中。看一个简单的神经元结构：

输入x1,x2,...,xn和权重系数做一个乘积，然后输入到神经元节点中，经过函数f的映射后得到结果作为下一个神经元的输入。这里的函数f就是一个激活函数，通过f的规则，来控制x1,x2,...,xn对后续神经元的输入量的多少。

OK，现在理解了激活函数具体是个什么东西了。那就要问为什么要有激活函数呢？没有激活函数神经网络work不？那它的作用是什么呢？

从网络上我们很容易得到结论——激活函数增加了模型的非线性！

那什么是模型的非线性呢？这里其实应该是这么说才更加的清晰——激活函数增加了模型的能力，使得它能够处理更加复杂的任务——这个就是模型的非线性。

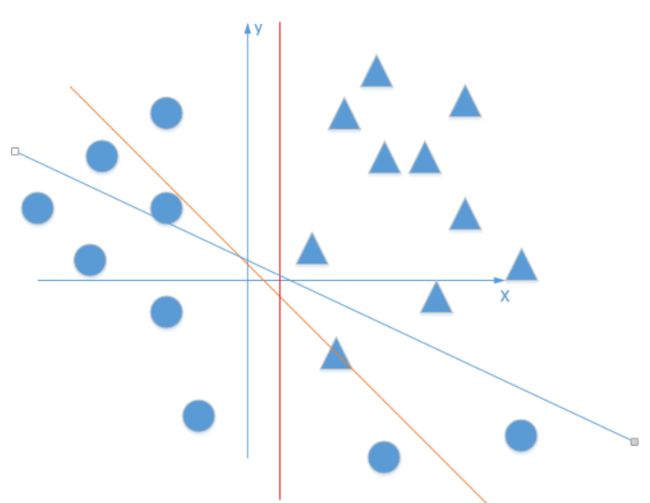
现在假设一个平面上的分类任务——图来自形象的解释神经网络激活函数的作用是什么？

这个任务使用不含激活函数的神经网络(简单的不含激活函数的多层感知器)来做的话，会是一个什么样的结果呢？

不含激活函数的神经网络——简单的不含激活函数的多层感知器——每个神经元不含那个f函数，那么这个神经网络的每一层都是很多个线性规划的组合，最后就相当于使用很多条直线来对上面这个平面进行分类，那么无论如何这个分类总是不能很好的区分开这些个点。

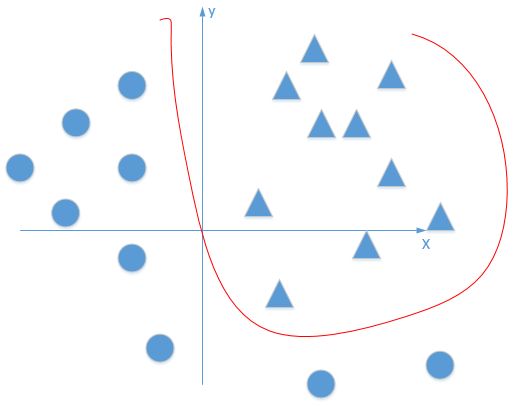
换言之也就是线性型的神经网络不能处理复杂任务，要想处理复杂任务就必须要增加神经网络的非线性——使用了激活函数的神经网络是可以拟合任意的曲线的。如下图——形象的解释神经网络激活函数的作用是什么？

这个时候的曲线就可以把这些点给区分开来，这里就增加了模型的能力。当然这样也有过拟合的风险。

简单总结一下，激活函数的作用就是增加模型的非线性——换言之就是增加模型的能力，让它能够处理更加复杂的任务。

当然作为激活函数，还有其他的一些必要性。神经网络一般都是深层网络，往往都会存在梯度爆炸和梯度消失的问题，表现出模型不能收敛，完成任务！这个时候激活函数也是可以作为解决这些问题的一个方法的，当然我认为也是很有效和很简单的方法。

二、激活函数的分类

在介绍激活函数的分类之前，很有必要了解一下神经网络梯度消失和梯度爆炸问题。神经网络采用BP算法，在设定好了权重和偏置初始参数，训练的过程中使用梯度下降法来更新权重参数。给定如下一个网络：

更新权重和偏置参数的时候有，根据链式求导法则

公式中的微分或者导数其实就是激活函数的导数，当和同时大于1的时候，深层的网络中，累积的乘会导致最终值非常大，从而导致梯度爆炸——权重剧烈变化——模型不能收敛；当和同时小于1的时候，累乘导致最后的结果趋近于0，这个时候就会出现梯度消失——权重变化很小或不会更新。

1、sigmoid

这是个比较老的函数，在机器学习中也是比较常用到的。直接看看它的公式和函数图像：

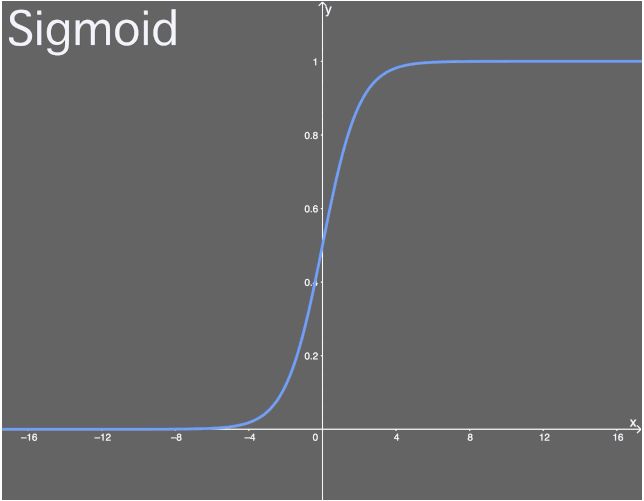
这里的Z就是输入，可以是单个的值也可以是其他变量的线性组合。函数图像：

可以看到它的定义域是无穷大，而值域是(0,1)。来看看该激活函数的导数，公式如下：

图像如下：

由上图可知，这里sigmoid函数的导数在输入X为极大值或者极限值的时候，导数几乎为0；从图上还可以看出倒数的值域是(0,0.25)的，x在(-2,2)的区间内，倒数值才大于0.10，如果x在这个区间之外，那么函数就不太敏感。这就会导致权重几乎不能更新，也就是产生梯度消失的问题，模型也就不能很好的训练了。

它作为激活函数的优点是什么呢？值域是(0,1)，同时又是单调单调函数，可以很好的把一个输入隐射到(0,1)之上。同时也是可导的，很适合作为一个激活函数。

另外一方面，这里的缺陷也很明显：

a、在输入很大的时候，它的倒数趋近于0，变化很小，这个就容易出现梯度消失问题，模型权重得不到更新。

b、它的输出不是0均值的，这个对于输出的分布的改变很有影响。

c、可以看着这个激活函数中含有指数的，计算速度上有一定的影响。网络模型训练的速度稍微慢一点。

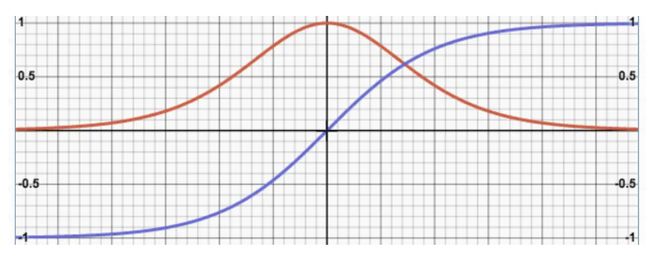
2、tanh激活函数

先看公式和图像

图像中蓝色曲线为原函数，红色曲线是导函数：

原函数图像以及导数和sigmoid函数的图像有点相像，比较明显的不同的地方就是导数的值域和变化快慢不一样。它同样存在梯度消失和计算量大的缺点，原因和上述sigmoid的函数解释一样的。当然它和sigmoid比较，也是具有一定的优势的：

a、导数值域大一些，相对而言它的非饱和区间要大一些。

b、值域是[-1,1]的，给出的输出肯定是0均值的。这个对训练也是有一定的好处的，数据的分布不会改变的太多。

3、RELU函数——Rectified Linear Unit——整流线性单元

在详细的学习这个激活函数之前，先简单的理解一下非线性。非线性就是一个函数在整个定义域上来说，一阶导数不是常数。

下面继续学习RELU函数

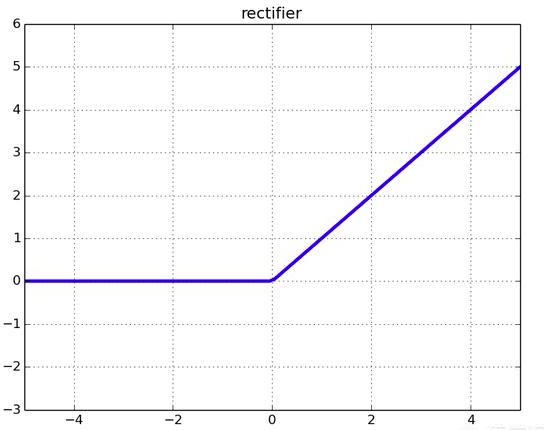
公式和导数公式及图像如下：

Relu(x)=max(0,x)

图像：

倒数图像

可以看到Relu函数在整个定义域上来看，它的导数不是常数，因此它具有非线性。

当x>0的时候，导函数值是1，这中情况下显然不会出现梯度消失的问题。

当x<0的时候，导数值为0，这个时候权重不会更新，这里也就出现了梯度消失的问题。

对比上面2个激活函数，relu激活函数的优点主要是：

a、首先运算成本上要小很多，因为不涉及到指数的运算

b、引入relu以后，也给神经网络引入了稀疏性——这里可以理解为激活的矩阵中含有很多0。这样能提高时间和空间复杂度。

也就是模型训练更快，当然模型的性能表现也更好。

缺点：

仍然可能存在梯度消失的可能，只要输入的特征都小于0；在梯度爆炸方面，由于激活函数的导数值是0或者1，权重就更新量就很大程度上由每一层的权重累乘决定。当设计好了神经网络的初始权重值，只要上下界处于(-1,1)之间，我认为就不会出现梯度爆炸的问题。

为了进一步的解决梯度消失的问题，学者们由提出了其他的一些激活函数，形式上和Relu是差不太多的。效率上比较快，同时又避免relu死亡饱和缺点的激活函数是Leaky ReLU。

4、Leaky ReLU

该函数的公式如下：

导函数公式如下：

可以看到当x<0的时候，它的导数值也是一个常数a，而且这个激活函数也没有涉及到指数之类的高运算成本。它和relu相比的优点就是完全解决了梯度消失的问题。当然同样这里也有个明显的缺点a是预定的，没有经过学习。

效果上来说，其实这个激活函数在神经网络上的表现和Relu是好不太多的。因为从大概率上来讲x<0的情况不是很多。

5、SELU

扩展型指数线性单元激活函数比较新，应用这个激活函数时，必须使用 lecun_normal 进行权重初始化，限制比较多。而且公式的证明也是非常复杂的。公式如下：

导函数：

它的参数和也是比较特殊的，参数论文推导出来的如下：

这个函数的优点如下：

• 内部归一化的速度比外部归一化快，这意味着网络能更快收敛；
• 不可能出现梯度消失或爆炸问题，见 SELU 论文附录的定理 2 和 3。

6、GELU

这个激活函数在Bert中应用的比较多，公式如下：

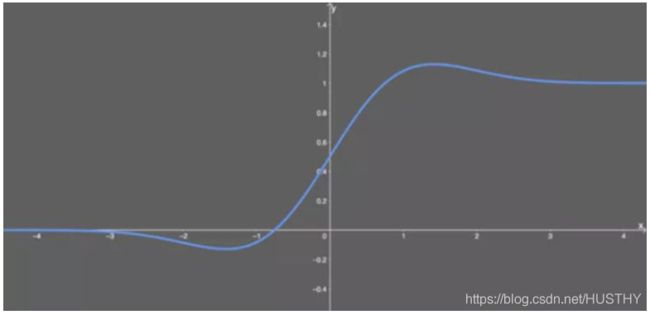
函数图像如下：

导函数如下：

优点如下：

• 似乎是 NLP 领域的当前最佳；尤其在 Transformer 模型中表现最好；
• 能避免梯度消失问题。

7、swish

这个激活函数也是谷歌团队提出来的，函数公式如下：

导数如下：

我们的实验证明 Swish 在多个深度模型上的性能持续优于或与 ReLU 函数相匹配。