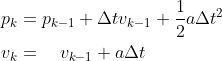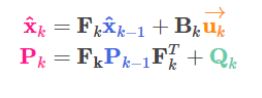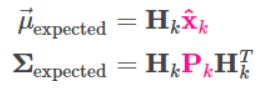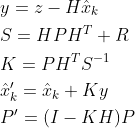深入浅出——零基础一文读懂DeepSORT(原理篇)
Intro
本文是笔者对DeepSORT算法学习的阶段性总结,基于笔者接触到的所有开源学习资料,辅以个人理解进行重新编排而成,力求清晰,使非专业的读者也能迅速对该算法原理有较为透彻的理解,便于后续代码学习。
笔者本人为非cs相关专业,论述不当之处欢迎指出。文中引用的博客均已在第0章中列出,在此致谢。如涉侵权敬请作者联系笔者删除。
0、参考博客
0.1 整体算法
博客1,MOT综述、算法流程,强烈推荐:https://zhuanlan.zhihu.com/p/97449724
博客2,带使用的函数的算法流程:https://zhuanlan.zhihu.com/p/80764724
博客3,源码讲解:https://zhuanlan.zhihu.com/p/90835266
博客4,流程图:人脸跟踪:deepsort代码解读_BigCowPeking-CSDN博客_deepsort源码
0.2 卡尔曼滤波
博客1:推荐您从一个小故事开始:如何通俗并尽可能详细地解释卡尔曼滤波? - 知乎
博客2:几个视频值得一看:如何通俗并尽可能详细地解释卡尔曼滤波? - 知乎
博客3:某位活菩萨翻译的外网博文:如何通俗并尽可能详细地解释卡尔曼滤波? - 知乎
1、多目标跟踪(MOT)综述
1.1 目标跟踪的任务分类
目标跟踪(Object Tracking)是计算机视觉领域的重要问题。按任务类型划分有如下几类。对于做交叉学科研究接触到这一领域的外行而言,最重要的是先搞明白自己的课题需求归属哪种任务场景。笔者的课题任务为MOT任务。
单目标跟踪(VOT/SOT):给定一个目标,追踪这个目标的位置。
多目标跟踪(Multiple Object Tracking,MOT):追踪多个目标的位置。
行人重识别(Person Re-ID):行人重识别是利用计算机视觉技术判断图像或者视频序列中是否存在特定行人的技术。广泛被认为是一个图像检索的子问题,即给定一个监控行人图像,检索跨设备下的该行人图像。旨在弥补固定的摄像头的视觉局限,并可与行人检测/行人跟踪技术相结合。
MTMCT:多目标多摄像头跟踪(Multi-target Multi-camera Tracking),跟踪多个摄像头拍摄的多个人。
姿态跟踪:追踪人的姿态。
以下是MOT任务与其他相关任务的区分:
1.2 MOT任务的解决方案及实现
MOT任务常见的解决方案主要有两种,即MFT 和 TBD。简介如下:
MFT:需要手动在初始帧中选择感兴趣区域,然后算法在第二帧开始的其余帧追踪这个目标。
TBD:基于检测的目标跟踪,是目标检测的后续任务。由于目标跟踪近几年的发展,成为常用方法。我们的DeepSORT也属于这类方法。
一般Tracking by Detection的实现主要分为如下步骤:
Object Localization:即Detection。在DeepSORT语境下,这一步相当于卡尔曼滤波的传感器。
Preprocessing:前处理,有NMS和置信度阈值两种(即抛弃confidence小于阈值的detection)
Feature Extraction:特征提取。在DeepSORT语境下,这部分是Re-ID模型对外观特征的提取。
Data Association:这一步是数据关联。在DeepSORT语境下,即对当前第k帧的detection和卡尔曼滤波中predict阶段根据前一帧k-1帧生成的track prediction匹配,在DeepSORT中是级联匹配和IOU匹配。
Track Management:包括卡尔曼滤波中的 track update,和对track的初始化、删除
Postprocessing: 后处理。
1、SORT 与DeepSORT
这一步建议读者先找到这两个算法的论文看,对这两个算法有个大概了解。一个简单的目标:读完至少知道这两篇论文各哪有几个小节(精确到二级标题),主要部件是哪些。
SORT和DeepSORT的优点特征是实现速度和准确性的tradeoff,因而倍受工业界青睐。本节接下来会给出这两个算法的关键流程图,读者看不懂也没有关系,看看关键部件如何组织即可。
1.1 SORT(Simple Online Realtime Tracking)
SORT是一个粗略的框架,核心就是两个算法:卡尔曼滤波和匈牙利匹配。
卡尔曼滤波:在图中被分为两个过程:预测和更新。预测过程:当一个小车经过移动后,且其初始定位和移动过程都是高斯分布时,则最终估计位置分布会更分散,即更不准确;更新过程:当一个小车经过传感器(也就是我们的Detections)观测定位,且其初始定位和观测都是高斯分布时,则观测后的位置分布会更集中,即更准确。但是由于我们得到的是一堆Track和一堆Detection,因此只有在用匈牙利算法进行分配后,才能把Track按照对应的Detection结果更新。
匈牙利算法:解决的是一个二分图分配问题(Assignment Problem),即如何分配使成本最小。在上图中是IOU Match那里,即基于IOU距离构造的成本矩阵对Detection和Track作匹配。SK-learn库的linear_assignment_和scipy库的linear_sum_assignment都实现了这一算法,只需要输入cost_matrix即代价矩阵就能得到最优匹配。不过要注意的是这两个库函数虽然算法一样,但给的输出格式不同。具体算法步骤也很简单,是一个复杂度 ![]() 的算法。
的算法。
SORT的问题:ID-switch很高,即同一个人的ID会变化。这主要是由于该算法论文3.4节中的一帧不匹配删除机制及IOU 成本矩阵的问题。
1.2 DeepSORT
主要特点:
1、加入外观信息,借用了ReID领域模型来提取外观特征(即标题中的Deep Association Metric),减少了ID switch的次数。
2、匹配机制从原来的基于IOU成本矩阵的匹配变成了级联匹配+IOU匹配(技术细节将在后续章节中讲解)。
2、卡尔曼滤波
2.1 Genreal Glimpse:
定义:利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响,所以这一最优估计也可看作是滤波过程。
输入->过程->输出:
输入:为k-1时刻的状态向量(nx1)和协方差矩阵(nxn);
过程:分predict和update两部分。predict基于先验的model(状态转移信息),如小车运动方程等,从k-1时刻根据model predict k时刻的状态和协方差;update是基于当下k时刻传感器(观测信息),对prediction进行更新。
输出:为k时刻的状态向量(nx1)和协方差矩阵(nxn)
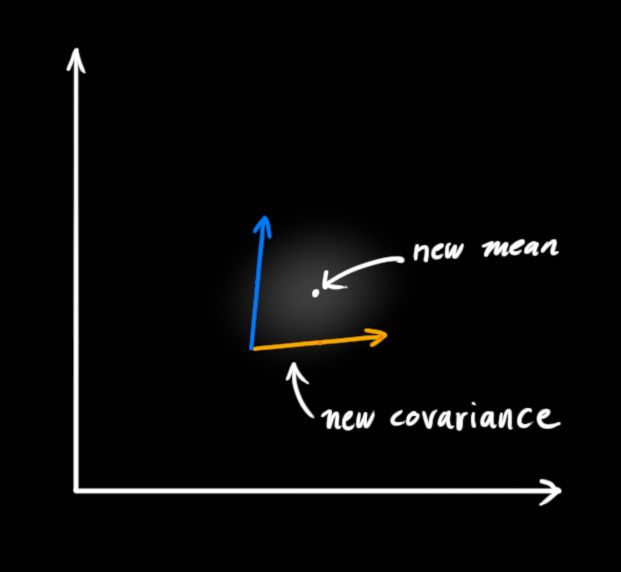
本质:Predict得到k时刻状态的一个高斯分布(一个高斯斑),观测得到k时刻状态的另一个高斯分布(另一个高斯斑)。因为无论传感器的观测还是模型的预测都会存在噪声,因此卡尔曼滤波器就是融合这两种信息,方法是将两个分布相乘,得到一个新的高斯斑。如下所示:
2.2 定性不定量地,illustration by an example
2.2.1 初始状态分布(高斯斑)
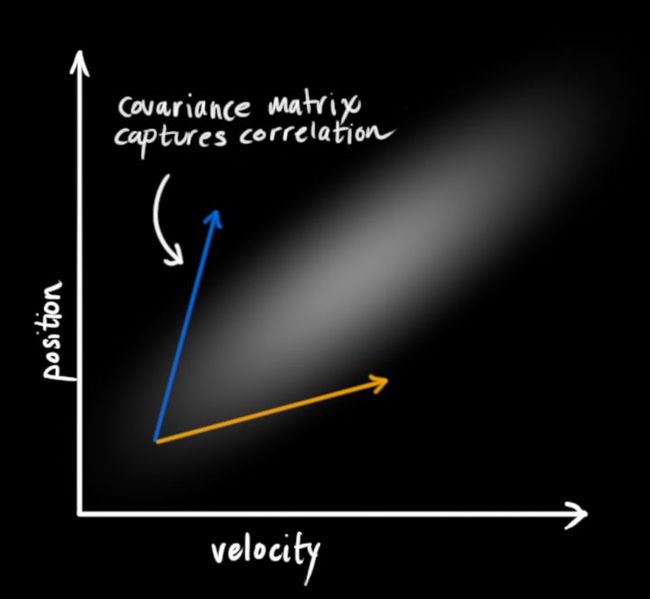
如下所示,以一辆小车的二维状态【位置,速度】为例,其某一时刻的状态分布(高斯斑)也许会长下图这样。
协方差描述了离散性。当状态量之间有所关联(如速度和位置分布其实是有关联的),高斯斑会长这样:
2.2.12 预测(Predict)
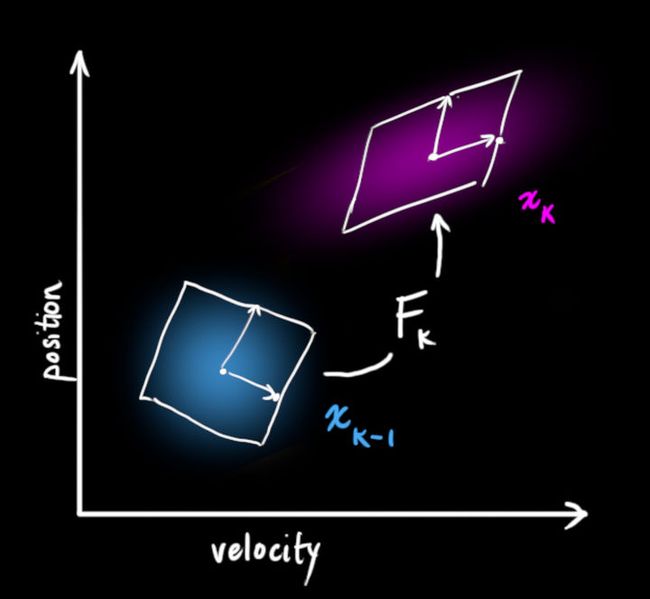
在知道了k-1时刻的状态分布![]() (状态分布自然包含状态和协方差,即“分布”)之后,基于model给出的状态转移我们可以预测k时刻的
(状态分布自然包含状态和协方差,即“分布”)之后,基于model给出的状态转移我们可以预测k时刻的![]() :
:
考虑外力作用下,基于牛顿力学(model)我们就可以得到如下的状态转移:
写成矩阵形式即:
以上![]() 为状态转移矩阵,
为状态转移矩阵,![]() 为控制矩阵,
为控制矩阵,![]() 为控制向量。特别注意的是我们这里状态向量只有两维,因此控制矩阵
为控制向量。特别注意的是我们这里状态向量只有两维,因此控制矩阵![]() 退化为向量,控制向量
退化为向量,控制向量![]() 退化为标量。
退化为标量。
以上即基于model的predict的确定性部分。很多时候这种predict是有噪声的,如一阵风吹过,小车经过下坡……都没用在model里考虑。如下图所示,原始状态中的每一个点可以都会预测转换到一个范围,而不是某个确定的点。所有的点经过转移后,构成的新分布协方差是放大的。假设![]() 分布里的每个点移动到一个符合方差
分布里的每个点移动到一个符合方差![]() 的新非高斯分布中:
的新非高斯分布中:
所有点:
因此考虑噪声之后,发散了:
因此,把predict中的不确定性假设为符合高斯分布的噪声,我们得到predict的最终结果即prediction:
2.2.3 Update by Sensor
引入传感器,我们有k时刻的读数。有以下两个问题:
1、传感器测量的可能并非我们要的那几个状态量,
2、传感器有一定误差。
针对第一点,例如,在DeepSORT中,Detection无法返回速度相关量。因此引入测量矩阵Hk,将观测向量映射到状态向量,这样我们就可以从传感器观测值得到对应的状态值。
针对第二点引入传感器的读数方差![]() 和读数均值
和读数均值![]() ,传感器的读数分布如下所示
,传感器的读数分布如下所示
所以现在我们有了两个高斯斑,一个来自于我们预测值,另一个来自于我们测量值。我们必须尝试去把两者的数据预测值(粉色)与观测值(绿色)融合起来。所以我们得到的新的数据会长什么样子呢?对于任何状态我们有两个可能性:
(1)传感器读数更接近系统真实状态
(2)预测值更接近系统真实状态。
如果我们有两个相互独立的获取系统状态的方式,并且我们想知道两者都准确的概率值,我们只需要将两者相乘。所以我们将两个高斯斑相乘,得到新的高斯斑:
2.3 计算公式
一般的卡尔曼滤波分为predict和update
predict
这一步给出的是预测值,也称先验状态估计值(a prior state estimate);
update
这一步给出的是状态的最优估计值,也称后验状态估计值(a posteriori state estimate)
以上K称为卡尔曼增益,是预测噪声和测量噪声的比较,详细见下面链接给出的推导。
kalman filter的详细推导过程参考:卡尔曼滤波(Kalman Filter)原理与公式推导 - 知乎,但其中有一些小错误。
在deepsort代码实现中也可以把上面三条公式写成下面的五条:
- 在上面的(1)中,z为detection的均值向量,不包含速度变化值,即z =[,,,],称为测量矩阵,它将track的均值向量
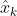 映射到测量空间,该公式计算detection和track的均值误差,y称为innovation (新息)。
映射到测量空间,该公式计算detection和track的均值误差,y称为innovation (新息)。 - 在(2)中,R为检测器的噪声矩阵,它是一个4x4的对角矩阵,对角线上的值分别为中心点两个坐标以及宽高的噪声,以任意值初始化。该公式先将协方差矩阵P映射到测量空间,然后再加上噪声矩阵R。
- (3) 计算卡尔曼增益,卡尔曼增益用于估计误差的重要程度。
- (4)和(5)得到更新后的均值向量
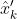 和协方差矩阵P'。
和协方差矩阵P'。
3、 匈牙利算法
匈牙利算法是用来解决二分图中的最优分配问题(Assignment Problem)的。像下图所示的给四个起重机分配四个任务就是典型的分配问题。有两类要素:
1、左边的表格是成本矩阵;
2、右边是约束。如图中所示,一个起重机只能做一个job,一个job只能一个起重机来做。
匈牙利算法在代码中很容易通过调用函数实现,这里不加解释地给出主要流程图。SK-learn库的linear_assignment_和scipy库的linear_sum_assignment都实现了这一算法,只需要输入cost_matrix即代价矩阵就能得到最优匹配。不过要注意的是这两个库函数虽然算法一样,但给的输出格式不同。
4、DeepSORT算法流程及其关键组件
再次给出DeepSORT的算法流程
4.1 Track的不同状态
如下所示,是track的三个状态。文中两个阈值取的是n_init=3,Amax=30.
4.2 级联匹配
目的:长时间遮挡中。卡尔曼滤波的prediction会发散,不确定性增加,而这样不确定性强的track的马氏距离反而更容易竞争到detection匹配。因此,需要按照遮挡时间n从小到大给track分配匹配的优先级。基于匈牙利算法。
输入为:
1、基于第k-1帧由卡尔曼滤波predict到的当前第k帧所有confirmed状态的track;
2、当前第k帧的所有detection
输出为:
1、match上的detection、track;
2、没有match上的track;
3、没有match上的detection。
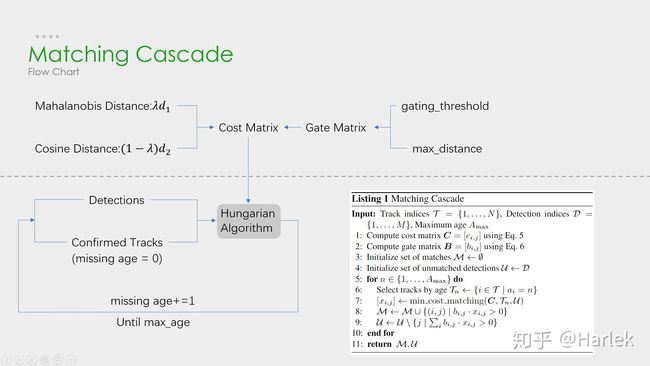
Listing 1讲解:
#input:基于第k-1帧由卡尔曼滤波predict到的当前第k帧所有confirmed状态的track索引T={1,...,N},当前第k帧所有detections D={1,...,M},最大未匹配帧数Amax=30
1.用外观最小余弦距离和马氏距离计算成本矩阵C(实操中lambda=0,只会用到外观最小余弦距离)
2.用外观最小余弦距离和马氏距离计算阈值矩阵B,用来滤掉不可能的匹配
3.用空集初始化match上的集合M
4.用D来初始化unmatch集合U
5. for n 属于 {1,...,Amax} : #n是每个track未匹配帧数
6. 从T中挑出一个子集Tn,即那些未匹配帧数=n的track的索引
7. 用匈牙利算法 对上一步选出的子集Tn和D进行匹配
8. 向M中添加匹配的序列号对(i,j),确保这个匹配满足阈值矩阵B(即bij=1)
9. 从未匹配索引集合U中删去匹配的序列号对(i,j)的j,确保这个匹配满足阈值矩阵B(即bij=1)
10. end
11. return M,U级联匹配流程图里上半部分就是特征提取和相似度估计,也就是算这个分配问题的代价函数。主要由两部分组成:代表运动模型的马氏距离和代表外观模型的Re-ID特征。
级联匹配流程图里下半部分匈牙利算法数据关联作为流程的主体。为什么叫级联匹配,主要是它的匹配过程是一个循环。从missing age=0的轨迹(即每一帧都匹配上,没有丢失过的)到missing age=30的轨迹(即丢失轨迹的最大时间30帧)挨个的和检测结果进行匹配。也就是说,对于没有丢失过的轨迹赋予优先匹配的权利,而丢失的最久的轨迹最后匹配。
论文关于参数λ(运动模型的代价占比)的取值是这么说的:
在我们的实验中,我们发现当相机运动明显时,将λ= 0设置是一个合理的选择。
因为相机抖动明显,卡尔曼预测所基于的匀速运动模型并不work,所以马氏距离其实并没有什么作用。但注意也不是完全没用了,主要是通过阈值矩阵(Gate Matrix)对代价矩阵(Cost Matrix)做了一次阈值限制。
4.3 IOU匹配
IOU匹配是在级联匹配之后做的东西,从SORT中继承而来,用来解决突然的外观变换导致级联匹配难以match的情况,如部分遮挡等。也是基于匈牙利算法做的。
输入:
1、candidate track,包括:
1.1 级联匹配中剩下的unmatched,n=1的track;
1.2 基于第k-1帧由卡尔曼滤波predict到的当前第k帧所有unconfirmed状态(即tenative)的track;
2、级联匹配中剩下的unmatched detection
输出:
1、match上的detection、track;
2、没有match上的track;
3、没有match上的detection。
然后进行更新处理,包括:
1、卡尔曼滤波 update track在第k帧状态的均值和方差
2、是否有track需要转为confirmed(到本帧match上且已连续命中3帧)
3、是否有要删除的track,即n>Amax
4、对unmatched detections分配新的track ID,为unconfirmed态即tenative态。
三者关系如下:
至此,关于DeepSORT的讲解基本结束。还有马氏距离、Re-ID模型等概念未加介绍,将后续更新附上。