【图像融合】主成分结合小波离散变换PCA-DWT图像融合【含Matlab源码 2199期】
⛄一、小波变换彩色图像融合简介
1 基于小波的图像融合
1.1 小波的分解和重构
小波变换是一种能够用来检测信号局部特征的数学工具。当然也可以将二维信号分解成不同分辨率的子带信号。由于图像为二维信号, 可以作以下小波分解:

其中, f (x, y) 为源图像, C0, H, G为一维小波滤波器, h, v, d分别代表水平、垂直和对角分量, H′, G′表示H, G的转置矩阵。
小波变换属于可逆变换, 可以通过以下方式实现信号的重构, 从而实现信号的恢复:

1.2 小波图像融合算法
该方法的基本思想是将待融合图像分解到不同频率上, 然后在不同频率上根据一定的规则完成信息的融合, 最后通过小波逆变换恢复图像。
基本的融合步骤描述如下:
(1) 配准待融合的源图像, 保证相关像素对齐。
(2) 将待融合图像各自完成小波分解, 如果进行层分解, 将会得到个高频子带和1个低频子带。
(3) 据不同融合规则完成高频和低频的系数融合, 低频采用平均法融合, 高频采用绝对值取大完成融合。
(4) 对步骤 (3) 得到的融合图像进行小波逆变换, 得到最终融合结果图像。
2 图像块清晰度的度量
2.1 主成分分析
主成分分析属于一种线性分析方法之一, 其被成功应用于人脸图像识别领域。它的主题思想是寻找最小均方意义下的逼近原始数据的最佳投影[。而对于数据的变异性和主成分分析中特征值的关系给出了证明。
数据矩阵C (标准化矩阵) 分解成正交矩阵U和V, V满足VTV=VVT=I:

由 (5) 式知, 描述变异性的分量ν1也可由特征值λ解释。
根据多聚焦图像的特征, 模糊区域类似于对该区域清晰图像实施了低通平滑滤波, 消除了图像中的部分高频信息, 所以模糊区域的高频局部变异较小, 而清晰区域高频部分变异较大。因此, 多聚焦图像相应像素块内高频信息变异大小可以作为清晰与否的判断依据, 即特征值越大, 图像越清晰。
2.2 图像块按清晰度分类
本文结合分块的思想依据, 将源图像进行区域的划分, 对每一区域块使用PCA分析法, 把特征值作为每一区域块的清晰与否的判定依据。
假设H1和H2为待融合的多聚焦图像P1和P2的高通滤波图像。邻域内像素一般情况下具有较强关联性, 因此, 为提高辨识的准确性, 进一步对H1和H2进行低通滤波, 得到A1和A2。假定Α1k, Α2k代表A1, A2的第k个子块图像, 根据PCA原理计算出AT1kA1k, AT2kA2k的第一主分量对应的特征值λk1, λk2, 则由下式得到描述图像清晰属性的标识矩阵:
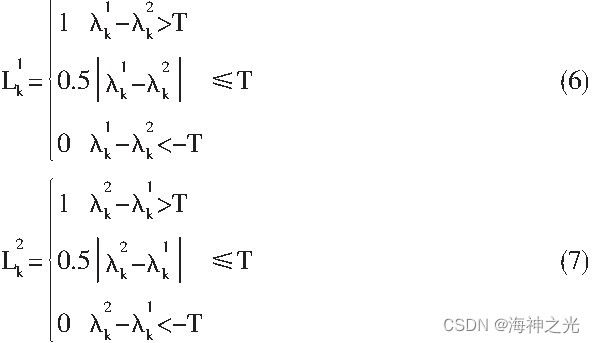
其中, T为阀值, Lk1, Lk2和是描述源图像P1和P2第k块清晰属性的标识, 如果为1表示此块是清晰, 为0表示此块模糊, 为0.5表示此块是属于两者间的边界区域。
3 图像融合方法
小波方法需要将整幅图像进行小波变换。考虑到多聚焦图像只有部分模糊的情况下, 这种变换就存在一定的冗余操作, 对于对应区域图像块都是清晰的情况, 此种变换就显得多余了, 而且会增加源图像和重构图像之间的偏差。因此考虑图像融合分成如下两部分来完成:
对于确定的清晰部分直接作为结果图像的对应部分, 即:

其中, Rk表示第k块结果图像块;、A1k, A2k为源图像P1和P2的第k块;Lk1、Lk2对应源图像第k块的标识元素。
对于介于清晰与模糊之间的区域采用小波法完成融合:

其中, F (A1k, A2k) 表示对子块A1k、A2k进行小波融合。
⛄二、部分源代码
clc; clear all;close all;
% Give number of input images
n=input(‘Number of images for fusion=’);
for i=1:1:n;
[imagefile1 , pathname]= uigetfile(‘.jpg;.bmp;’,‘Open file Eye image’);
name=[pathname,imagefile1];
if imagefile1 ~= 0
a{i} = double(imread([name]));
[row,col,dim]=size(a{i});
if (dim>2)
a{i} = double(rgb2gray(imread([name])));
va{i}=cov(a{i},a{i});
end
end;
[ca{i},ch{i},cv{i},cd{i}] = dwt2(a{i},‘db3’);
vadwt{i}=cov(ca{i},ca{i});
vhdwt{i}=cov(ch{i},ch{i});
vvdwt{i}=cov(cv{i},cv{i});
vddwt{i}=cov(cd{i},cd{i});
avdwt{i}=(vadwt{i}+vhdwt{i}+vvdwt{i}+vddwt{i})/n;
end
% Evaluation of principal components for the relevant coefficients
[fca m1]=fuse_pcaany(ca,n);
[fch m2]=fuse_pcaany(ch,n);
[fcv m3]=fuse_pcaany(cv,n);
[fcd m4]=fuse_pcaany(cd,n);
% principal component averaging
for i=1:1:n;
pc(i)=(m1(i,1)+m2(i,1)+m3(i,1)+m4(i,1))/4;
end
[z3 s3]=size(a{1});
out=zeros(z3,s3);
% Fusion based on average of principal components
for i=1:1:n
dwtpcav = pc(i)*a{i};
out=out+dwtpcav;
end
figure,
for i=1:1:n
subplot(1,n+1,i)
imshow(a{i},[]);
title([‘原图’,num2str(i)])
end
⛄三、运行结果
⛄四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1]向昌成,杨兴江,李清茂.PCA和小波在多聚焦图像融合中的应用研究[J].阿坝师范高等专科学校学报. 2011,28(02)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除

