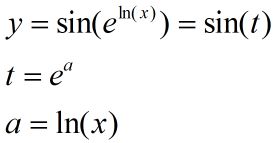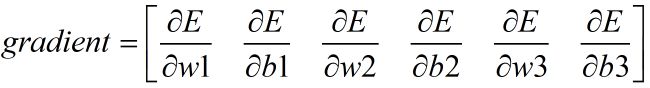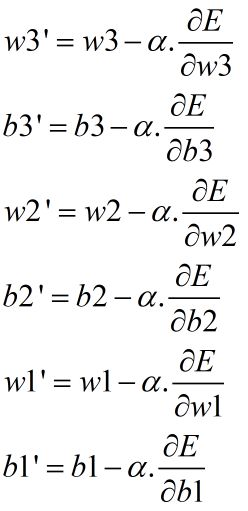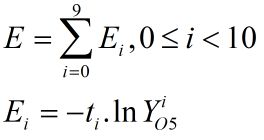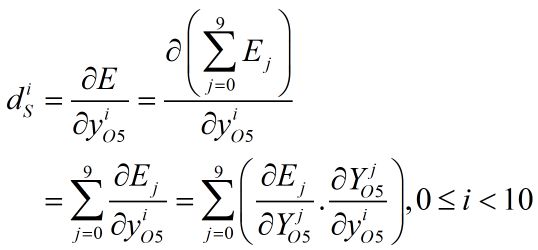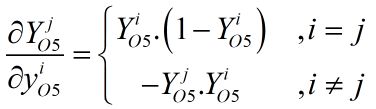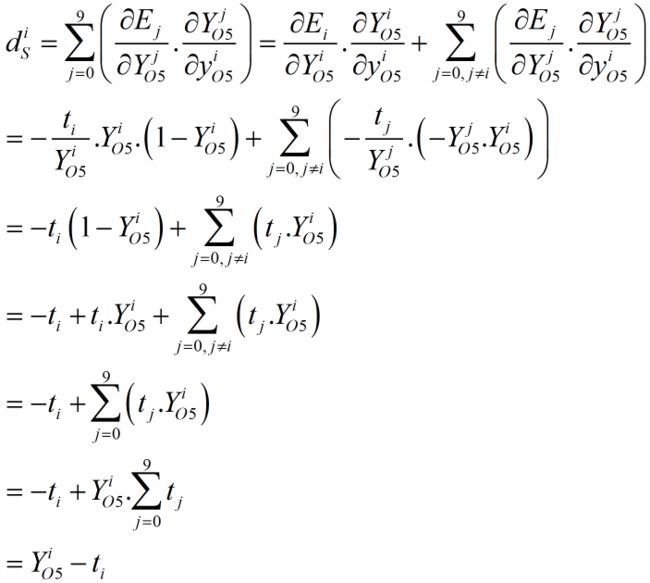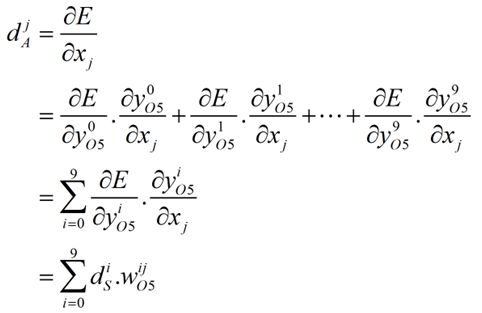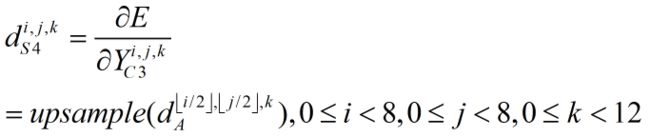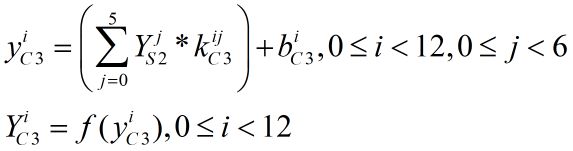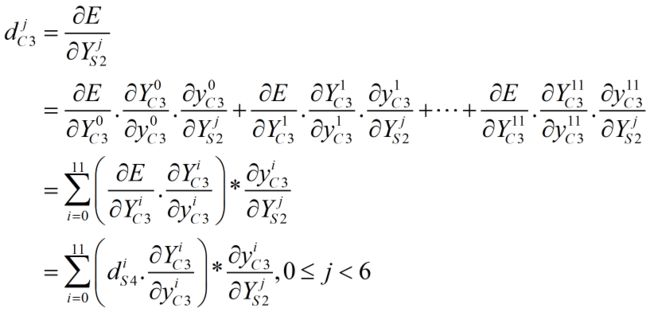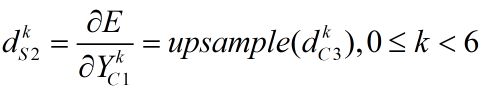卷积神经网络原理及其C++/Opencv实现(4)—误反向传播法
转眼,这一系列的文章我们已经更新到第4篇了,在此列出前面三篇的超链接,方便读者跳转阅读:
1. 卷积神经网络原理及其C++/Opencv实现(1)
2. 卷积神经网络原理及其C++/Opencv实现(2)
3. 卷积神经网络原理及其C++/Opencv实现(3)
误反向传播的过程,也就是误差信息从网络末端的Softmax层向网络起始端的C1层传播的过程。接上篇文章的内容,本文我们将从数学公式的角度详细推导一下5层网络的误反向传播的过程。
1. 误反向传播的一个简单例子
下面我们首先举个简单的例子来说明误反向传播的原理与目的。
(1) 最优化模型
假设我们有函数E=f(x),E是关于x的复合函数:
很明显,在以上E函数的计算过程中,x为输入信号,y3为输出信号,t为x的标签(也即输入x之后我们期待得到的输出值)。最终得到的E函数值越小,说明y3与t越接近,也即输出信号越符合我们的期待。所以我们的目的就很清晰了:求使E函数取得最小值的参数w1、b1、w2、b2、w3、b3。
看到这里,是不是觉得这就是一个典型的最优化问题?是的,没错!把函数E当作目标函数值,为了使E函数求得最小值,可以使用梯度下降法对其参数进行优化。
(2) 为什么使用误反向误差传播法
梯度下降法的最优化原理,我们在之前的文章已经讲过,其关键是求得参数的梯度(偏导数),然后沿着梯度的反方向更新参数。
梯度下降法详解
当目标函数不复杂时,我们通常使用差分法来求参数的近似梯度值,其中eps为一个较小的值,比如0.1或0.5。
由上式可知,计算一个参数的偏导数需要计算两次目标函数值。当目标函数很复杂时(比如深度学习网络),其本身的计算相当耗时,再加上参数的个数很多,对应的需要计算的偏导数也很多。这样一来,每次优化参数时在计算偏导数上面就耗费了大量时间,导致优化参数的效率极其低下。
基于以上原因,聪明的人们又想出了另一种计算参数梯度的方法:误反向传播法:一层一层地计算梯度,从后向前,使用后一层的梯度信息来计算前一层的梯度。这样一来就避免了通过计算目标函数值来计算梯度。
(3) 复合函数的链式求导法则
误反向传播法应用了复合函数的求导法则,首先我们来讲一下复合函数的求导原理。我们可以把复合函数理解成不同函数的嵌套,要求复合函数中某一变量的导数时,需要一层一层的求导,然后把各层的求导结果相乘,就是最终的求导结果。比如有一个关于x的复合函数y:
那么求y关于x的导数如下:
(4) 误反向传播的过程
首先,列出需要求解的梯度如下:
根据链式求导法则,首先是求w3、b3的梯度:
其次,求w2、b2的梯度:
最后,求w1、b1的梯度:
观察上述计算可以知道,链式求导是一个累乘的过程,不过当前层的部分累乘因子并不需要全部计算,因为上一层已经算好了:
比如我们记:
其中d3为误差信息,它从神经网络的末端传输到起始段的过程,就是误反向传播的过程。如下图所示:
我们称d1、d2、d3为局部梯度,也就是说,每一层的局部梯度就是最终的目标函数对本层的输入信号的偏导数(比如E的输入信号是y3,y3的输入信号是y2,y2的输入信号是y1)。得到这些局部梯度之后,从而得到各个参数的梯度:
得到参数的梯度之后,就可以沿着梯度反方向更新参数啦,其中α为学习率,通常设定一个合适的经验值,然后随着迭代的增加而减小。
2. 5层卷积神经网络的误反向传播过程
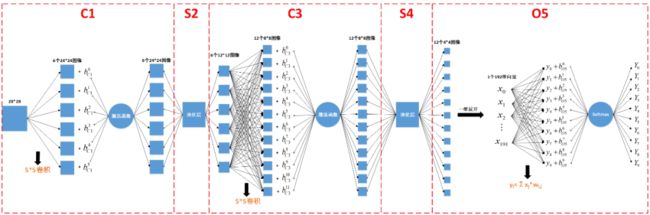
由上篇文章可知,5层神经网络的最后一层是全连接层,该层又可以分为Affine层与Softmax层,因此5层网络又可以细分为6层网络,再加上衡量输出信号是否符合期待的交叉熵误差函数,一共7层。从起始段到末端依次是:卷积层C1-->池化层S2-->卷积层C3-->池化层S4-->Affine层-->Softmax层-->交叉熵误差函数E。
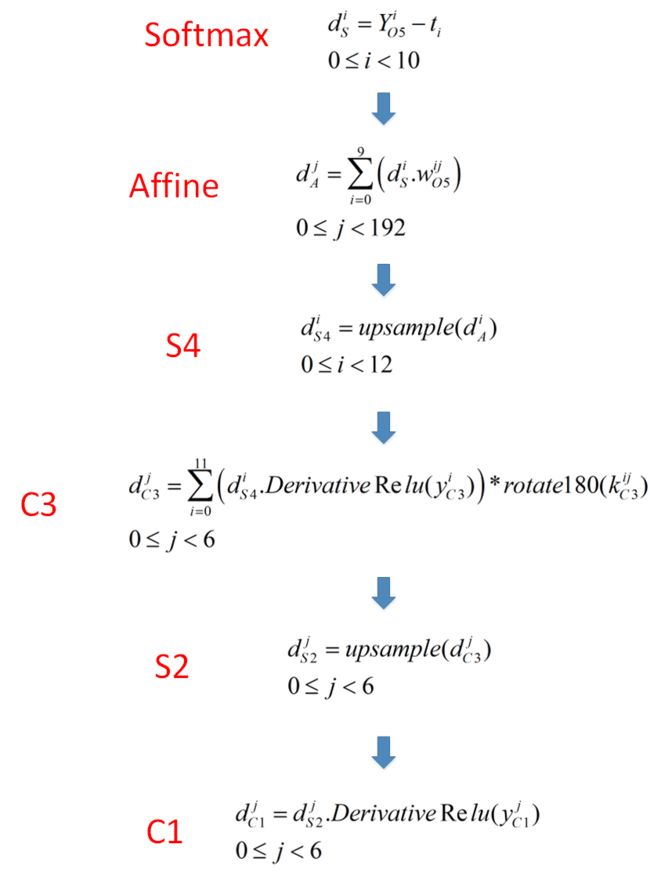
接下来我们来讲这7层网络的误反向传播过程。如下图所示:
(1) Softmax层局部梯度的计算
前面文章已经讲过,交叉熵误差函数的表达式为:
其中t为标签,Y为Softmax函数的输出,y即是Affine层的输出也是本层的输入:
该层的局部梯度为:
求E关于Y的偏导数:
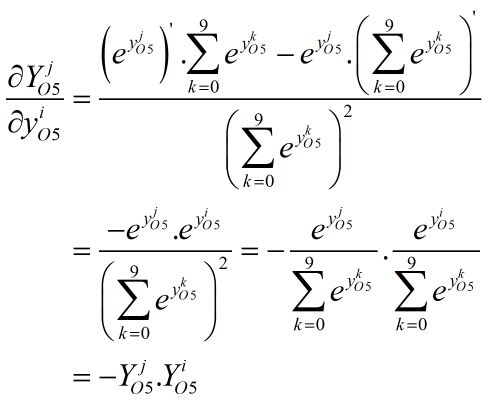
接着求Y关于y的偏导数,这里分为两种情况:
a. 首先是i=j的情况:
a. 其次是i≠j的情况:
综合以上两种情况有:
所以有本层局部梯度的计算:
(2) Affine层局部梯度的计算
Affine层的正向传播计算式如下式,其中y为Affine层的输出,x是S4层的输出信号也是本层的输入信号:
现在,我们来求O5层的局部梯度。首先,为了看清复合函数的层次关系,我们画出以下关系图:
由上图可以看出来,E与10个Y都有关系、每个Y与10个y都有关系、每个y都与所有x都有关系,因此求本层的局部梯度,也就是求E关于x的偏导数时,根据复合函数的求导法则可按下式计算,其中0≤j<192。
(3) 池化层S4局部梯度的计算
池化层的正向传播是一个向下采样的过程,也即数据量减少了。如果是反向传播呢,很容易想到,那就是向上采样的过程了,也即恢复向下采样之前的数据量。比如下图:
首先,我们要知道,S4层输出的12个4*4图像,被按顺序展开成长度为12*4*4=192个数据,然后再输入O5层。所以反向传播时,O层输出的对应的192个局部梯度,又被按顺序转成12个4*4矩阵,然后传入S4层。
由于池化模式分为均值池化与最大值池化,反向传播也有对应的两种传播方式,下面我们分别阐述原理(假设池化窗口为2*2)。
a. 均值池化的反向传播
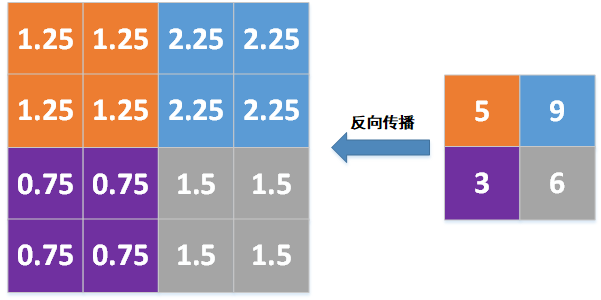
如果是均值池化模式,则把局部梯度除以池化窗口的尺寸2*2=4,然后把除以尺寸的结果填充到对应的2*2窗口,如下图所示:
其中:
5/4=1.25
9/4=2.25
3/4=0.75
6/4=1.5
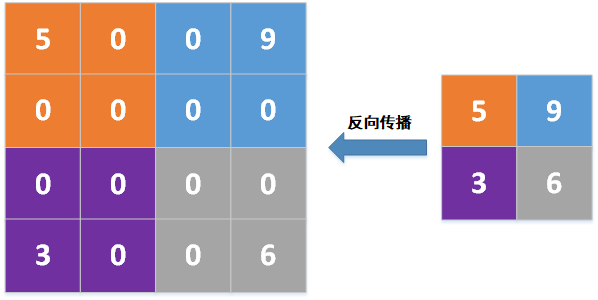
a. 最大值池化的反向传播
如果是最大值池化模式,则把局部梯度放到池化之前池化窗口中的最大值位置,然后其它位置填充0,比如池化窗口2*2,池化前,池化窗口中最大值的位置分别为左上、右上、左下、右下,则向上采样后为:
由上述可知,经过池化层S4的反向传播之后,12个4*4的局部梯度变成12个8*8的局部梯度,如下式,其中⌊⌋为向下取整符号,比如⌊3/2⌋=⌊1.5⌋=1。
上述是针对每个值的计算,如果写成矩阵的形式则如下,其中dS4为8*8矩阵,dA为4*4矩阵。
(4) 卷积层C3局部梯度的计算
前面的文章我们已经讲过,C3层输入的是S2层传来的6个12*12图像,其正向传播的计算式如下,其中"*"为图像的卷积操作,f为Relu激活函数,Y、y、k均表示二维矩阵。b表示一个偏置值,矩阵加上该偏置的操作相当于矩阵中每个值都加上该偏置,因此结果还是一个矩阵。同理,矩阵输入Relu激活函数的操作,相当于矩阵中每个值都输入激活函数,从而每个值的输出还是组成一个相同维度的输出矩阵。
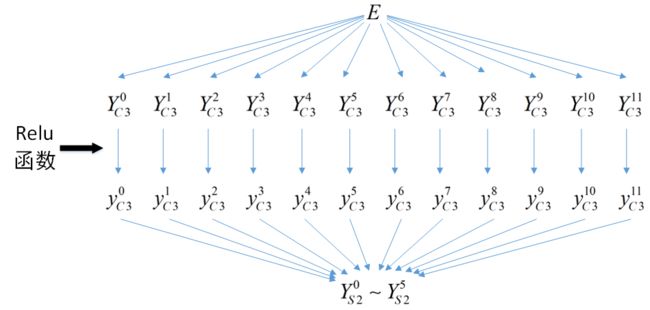
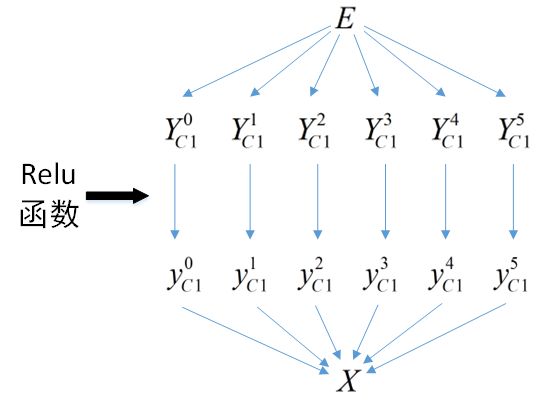
以下是目标函数E与本层的输入、输出信号关系图,由此可以知道E与所有YC3有关系、每个YC3只与对应的一个yC3有关系、每个yC3与所有YS2都有关系。
根据复合函数的求导法则,本层的局部梯度可按下式计算:
首先我们求YC3关于yC3的偏导数。我们使用的激活函数为Relu函数,其表达式以及导数表达式如下。其中YC3和yC3都是8*8矩阵(0≤r<8,0≤c<8)。直观说,正向传播时就是矩阵yC3的每个数值输入Relu函数并输出一个值,所有输出值组成相同维度的YC3矩阵。矩阵yC3的偏导数也类似,对于yC3的每个数值,如果大于0则其导数为1,否则为0,所有导数值同样组成相同维度的导数矩阵。
接下来是求yC3关于YS2的偏导数。由于yC3是由YS2经过卷积运算得到的,反向传播时也同样是卷积运算(注意到上述dC3的计算式中有个"*"号,这表示矩阵的卷积运算)。这里我们只放出结论(具体推导我们再另外深究):
上式中的rotate180表示将矩阵顺时针旋转180°,比如:
于是有:
上式中的"."表示两个矩阵的对应位置数值相乘,结果还是相同维度的矩阵,"*"表示两个矩阵的卷积,由于正向传播的卷积模式为Valid模式,一张12*12的图像经过卷积之后输出(12-5+1)*(12-5+1)=8*8的卷积结果图像,那么为了使8*8图像恢复为12*12图像,反向传播使用Full卷积模式,输出(8+5-1)*(8+5-1)=12*12图像。
(5) 池化层S2局部梯度的计算
本层的反向传播原理与S4一样,都是池化的逆操作,也即向上采样。
从C3层传过来的局部梯度是6个12*12矩阵,经过本层后,得到6个24*24矩阵,如下式,其中dC3为12*12矩阵,dS2为24*24矩阵。
(6) 卷积层C1局部梯度的计算
C1层输入1个28*28的图像X,其正向传播的计算式如下,其中"*"为图像的卷积操作,f为Relu激活函数,Y、y、k均表示二维矩阵,b表示一个偏置值。
本层与目标函数的层次关系为:
需要注意的是,本层是5层网络的起始层,所以误差信息反向传播到这里就停止了,不需要再往前一层传播(没有前一层)。所以本层只需要求E关于y的偏导数即可,不需要求E关于X的偏导数。
上式中,d、Y、y都是矩阵,"."为两个矩阵中对应位置的值相乘,因此结果是一个相同维度的矩阵。
好了,误差信息的反向传播就传播到这里,接下来我们来总结一下吧,如下图所示:
下篇文章我们来讲怎么使用局部梯度更新神经网络的参数,敬请期待!
欢迎扫码关注以下微信公众号,接下来会不定时更新更加精彩的内容噢~