算法篇-------贪心2

题目1-------活动选择

有n个需要在同一天使用同一个教室的活动a1, a2, …, an，教室同一时刻只能由一个活动使用。每个活动a[i]都有一个
开始时间s[i]和结束时间f[i]。一旦被选择后，活动a[i]就占据半开时间区间[s[i],f[i])。如果[s[i],f[i])和[s[j],f[j])互不重
叠，a[i]和a[j]两个活动就可以被安排在这一天。求使得尽量多的活动能不冲突的举行的最大数量。

怎么考虑呢？
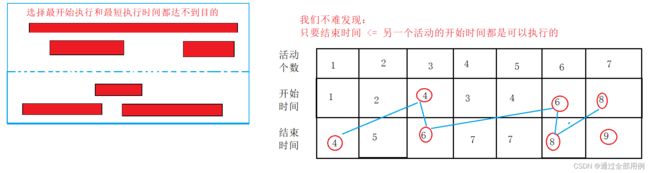
我们优先考虑结束时间最早的活动，结束时间最早意味着能安排更多的活动。
贪心-------通过一系列的局部最优达到总体最优，（只考虑眼前）

选择最早开始和最短时间都不能达到目的。例如下面的3个活动：

代码分享：

class Sort
{
public:
	bool operator()(vector<int> a, vector<int> b)
	{
		return a[1] < b[1];
	}
};

//vv是已经按照最短结束时间排序好的
int get_max_act(const vector<vector<int>>& vv)
{
	int cnt = 1;
	int endtime = vv[0][1];
	for (int i = 1; i < vv.size(); i++)
	{
		//可以安排下一个活动了
		//下一个活动的起始时间大于当前活动的结束时间
		if (vv[i][0] >= endtime) 
		{
			endtime = vv[i][1];
			cnt++;
		}
	}

	return cnt;
}

题目2-----无重叠区间

力扣题：435

这一题和上面一题的思路一样， 优先选择结束区间最小的，使之能有更多的区间，然后达到删除最小区间的目的。
也就是说，通过一系列的局部最优达到整体最优。

class Solution {
public:
    class Sort
    {
    public:
           bool operator()(const vector<int>& a, const vector<int>& b)
           {
               return a[1] < b[1];
           }
    };

    int eraseOverlapIntervals(vector<vector<int>>& intervals) 
    {
        if(intervals.empty())
            return 0;

        sort(intervals.begin(), intervals.end(), Sort());
        int end = intervals[0][1];
        int num = 1;
        for(int i = 1; i < intervals.size(); i++)
        {
            if(intervals[i][0] >= end)
            {
                end = intervals[i][1];
                num++;
            }
        }

        return intervals.size()- num;

    }
};

题目3------最多可以参加的会议数目

力扣：1353

这个题和上面几个题有些不同，上面的是时间间隔， 而这一题用的是其中某一天
也就是说，在1-----10 0001天我们都是可以去开会议的。
怎么去选择会议呢？ 优先选择开始时间最早，结束时间最短的。

这个题的核心思路是：
优先选择开始时间最早， 但是呢很多会议也会存在开始时间一样的情况，所以呢我们再次进行选择，选择结束时间最早的。

这一题稍微有一些复杂，所以提供了不少的注释
代码：

class Solution {
public:
    int maxEvents(vector<vector<int>>& events) 
    {
        //因为开始时间的范围是在1--10^5
        vector<vector<int>> vv(100001);
        
        //按照起始实际按分类，将第i个会议分到同一个一维数组
        for(int i = 0; i < events.size(); i++)
            vv[events[i][0]].push_back(i);
        
        //优先队列类型是int， 容器是适配器用vector， 采用小堆
        int ans = 0;
        priority_queue<int, vector<int>, greater<int>> pq;

        //遍历所有可以执行的时间，看看某一个会议能不能在这一天去执行
        for(int i = 0; i < 100001; i++)
        {
            for(auto e : vv[i])  //e是开始时间为vv[i]的第几个会议
              pq.push(events[e][1]);   //将其结束时间入队列
            
            //i表示当前执行的时间，而队列存放的是结束时间
            //只要比i小的结束时间表明该会议已经错过了
            while(!pq.empty() && pq.top() < i)
               pq.pop();
            
            //从里面找出一个会议结束时间最早的出来开。
            if(!pq.empty())
            {
                ans++;
                pq.pop();
            }
        }
        
        return ans;
    }
};

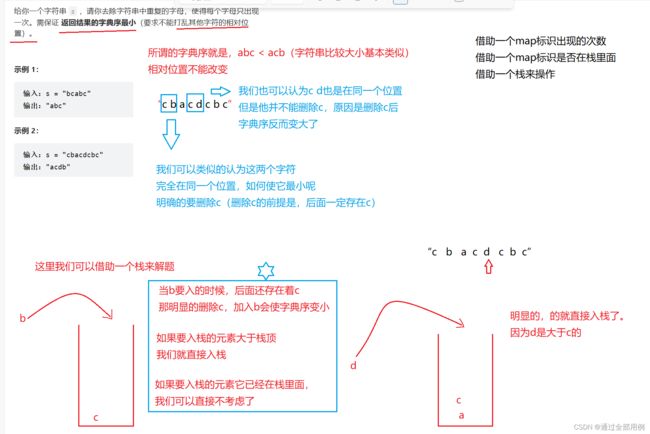
题目4-------去除重复字母

力扣题：316

class Solution {
public:
    string removeDuplicateLetters(string s) 
    {
        unordered_map<char, int> cnt;
        unordered_map<char, bool> inst;
        stack<char> st;

        for(auto e : s)       //用map统计次数
              cnt[e]++;

        for(int i = 0; i < s.size(); i++)
        {
            char c = s[i];
            if(inst[c])  //要操作的元素已经在栈里面，默认已经放好了
            {
                cnt[c]--;
                continue;
            }
           
            //如果当前操作的元素小于栈顶元素，并且栈顶元素还存在
            while(!st.empty() && c < st.top() && cnt[st.top()] > 0)
            {
                inst[st.top()] = false; //出栈了，栈顶元素肯定就不在栈了
                st.pop();
            }
            
            inst[c] = true; //入栈后就改状态
            st.push(c);
            cnt[c]--;
        }
        
        string ans;
        while(!st.empty())
        {
            ans += st.top();
            st.pop();
        }
        
        reverse(ans.begin(), ans.end()); //需要逆序操作的
        return ans;
    }
};

题目5------移掉K位数字

力扣题：402

class Solution {
public:
    string removeKdigits(string num, int k)
    {
         string ans;
         stack<char> st;

         for(int i = 0; i < num.size(); i++)
         {
             char c = num[i];
             
             //当前操作的元素 < 栈顶元素 &&  有删除的机会 k > 0 
             while(!st.empty() && c < st.top() && k > 0)
             {
                 st.pop();
                 k--;
             }
            
            //栈位空， 当前为0，直接不考虑
            if(st.empty() && c == '0')
                   continue;

             st.push(c);
         }
           
         while(!st.empty() && k--)   //如果还有删除的机会，直接删除
             st.pop();

        while(!st.empty())
        {
            ans += st.top();
            st.pop();
        }
        reverse(ans.begin(), ans.end());
        
        if(ans.empty())
              ans += "0";

        return ans;     
    }
};

题目6-----拼接最大数

力扣321

这一个题目代码虽然有一些长，但是逻辑比较简单，并不复杂。

class Solution {
public:

    //k是需要移除的个数
    vector<int> subNumber(const vector<int>& v, int k)
    {
        vector<int> ans;
        stack<int> st;
        for (int i = 0; i < v.size(); i++)
        {
            int c = v[i];

            while (!st.empty() && c > st.top() && k > 0)
            {
                st.pop();
                k--;
            }

            st.push(c);
        }

        while (!st.empty() && k > 0)
        {
            st.pop();
            k--;
        }

        while (!st.empty())
        {
            ans.push_back(st.top());
            st.pop();
        }

        reverse(ans.begin(), ans.end());
        return ans;
    }

    // v1 >= v2 返回true
    bool cmpArray(const vector<int>& v1, int i, const vector<int>& v2, int j)
    {
        while (i < v1.size() && j < v2.size())
        {
            if (v1[i] > v2[j])
                return true;

            if (v1[i] < v2[j])
                return false;

            i++;
            j++;
        }

        //走到这里， 无非就是一个为空， 一个不为空
        if (j == v2.size())
            return true;

        return false;
    }

    vector<int> mergeArray(const vector<int>& v1, const vector<int>& v2)
    {
        int i = 0, j = 0;
        vector<int> ans;

        while (i < v1.size() && j < v2.size())
        {
            if (cmpArray(v1, i, v2, j))
            {
                ans.push_back(v1[i]);
                i++;
            }
            else
            {
                ans.push_back(v2[j]);
                j++;
            }
        }

        while (i < v1.size())
        {
            ans.push_back(v1[i++]);
        }

        while (j < v2.size())
        {
            ans.push_back(v2[j++]);
        }

        return ans;
    }

    vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k)
    {
        //下面一个数组拿出多少个元素，另一个数组拿出一个元素边界不好控制
        //我们用举例来： m = 4 , n = 6,显然对于nums2来说
        //最少拿出一个元素， 最多拿出5个元素
        int m = nums1.size(), n = nums2.size();
        int begin = max(0, k - m), end = min(k, n);

        vector<int> ans;
        for (int i = begin; i <= end; i++)
        {
            //对于nums2来说，拿出i个元素， 去掉n - i 个元素
            //对于nums1来说，就要拿出k - i个， 去掉m - k + i个元素
            vector<int> subnum1 = subNumber(nums2, n - i);
            vector<int> subnum2 = subNumber(nums1, m - k + i);

            vector<int> ret = mergeArray(subnum1, subnum2);
            if (cmpArray(ret, 0, ans, 0))
                swap(ret, ans);  //c++11支持右值引用，可以窃取资源
        }

        return ans;
    }
};