决策树分类算法进阶(一)28
1、决策树概述
决策树是属于有监督机器学习的一种,起源非常早,符合直觉并且非常直观,模仿人类做决策的过程,早期人工智能模型中有很多应用,现在更多的是使用基于决策树的一些集成学习的算法。这一章我们把决策树算法理解透彻了,非常有利于后面去学习集成学习。
1.1、示例一
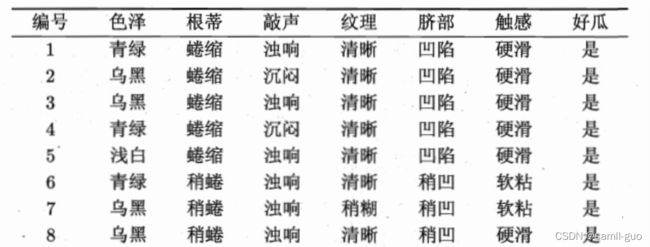
我们有如下数据:
| ID | 拥有房产(是/否) | 婚姻[单身,已婚,离婚] | 年收入(单位:千元) | 无法偿还债务(是/否) |
|---|---|---|---|---|
| 1 | 是 | 单身 | 125 | 否 |
| 2 | 否 | 已婚 | 100 | 否 |
| 3 | 否 | 单身 | 70 | 否 |
| 4 | 是 | 已婚 | 120 | 否 |
| 5 | 否 | 离婚 | 95 | 是 |
| 6 | 否 | 已婚 | 60 | 否 |
| 7 | 是 | 离婚 | 220 | 否 |
| 8 | 否 | 单身 | 85 | 是 |
| 9 | 否 | 已婚 | 75 | 否 |
| 10 | 否 | 单身 | 90 | 是 |
上表根据历史数据,记录已有的用户是否可以偿还债务,以及相关的信息。通过该数据,构建的决策树如下:

比如新来一个用户:无房产,单身,年收入55K,那么根据上面的决策树,可以预测他无法偿还债务(蓝色虚线路径)。从上面的决策树,还可以知道是否拥有房产可以很大的决定用户是否可以偿还债务,对借贷业务具有指导意义。
1.2、示例二
女孩母亲要给她介绍对象,年龄是多少,母亲说24。长得帅吗?挺帅的。收入高吗?中等收入。是公务员吗?母亲说,是的。女孩:好,我去见见。
问题:图片是二叉树吗?
决策树是标准的二叉树,每个节点只有两个分支~
- 上面那棵树中,属性:绿色的节点(年龄、长相、收入、是否是公务员)
- 属性叫做,data,数据,一般使用X表示
- 跟属性对应,目标值(橘色节点),一般使用y表示
- 构建这棵树时,先后顺序,每个人,标准不同,树结构不同
- 计算机,构建树,标准一致的,构建出来的树,一致
1.3、决策树算法特点
-
可以处理非线性的问题
-
可解释性强,没有方程系数 θ \theta θ
-
模型简单,模型预测效率高 if else
2、DecisionTreeClassifier使用
2.1、算例介绍
其中s、m和l分别表示小、中和大。
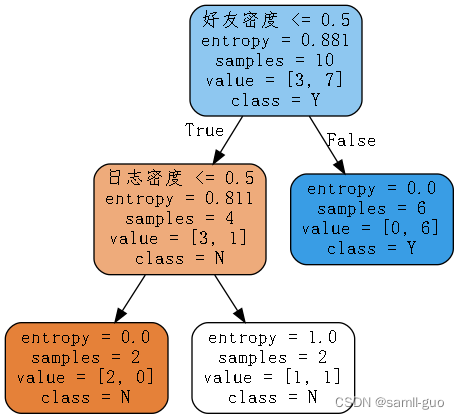
账号是否真实跟属性:日志密度、好友密度、是否使用真实头像有关系~
2.2、构建决策树并可视化
数据创建
import numpy as np
import pandas as pd
y = np.array(list('NYYYYYNYYN'))
print(y)
X = pd.DataFrame({'日志密度':list('sslmlmmlms'),
'好友密度':list('slmmmlsmss'),
'真实头像':list('NYYYYNYYYY'),
'真实用户':y})
X
模型训练(报错,原因:数据类型是字符串)
from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier()
model.fit(X,y)
数据修改(map函数,进行数据转换)
X['日志密度'] = X['日志密度'].map({'s':0,'m':1,'l':2})
X['好友密度'] = X['好友密度'].map({'s':0,'m':1,'l':2})
X['真实头像'] = X['真实头像'].map({'N':0,'Y':1})
X
模型训练可视化
import matplotlib.pyplot as plt
# 使用信息熵,作为分裂标准
model = DecisionTreeClassifier(criterion='entropy')
model.fit(X,y)
plt.rcParams['font.family'] = 'STKaiti'
plt.figure(figsize=(12,16))
fn = X.columns
_ = tree.plot_tree(model,filled = True,feature_names=fn)
plt.savefig('./iris.jpg')
数据可视化另一种方式,安装教程
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
import graphviz
from sklearn import tree
model = DecisionTreeClassifier(criterion='entropy')
model.fit(X,y)
dot_data = tree.export_graphviz(model, out_file=None,
feature_names= X.columns,# 特征名
class_names=np.unique(y),# 类别名
filled=True, # 填充颜色
rounded=True) # 圆角
graph = graphviz.Source(dot_data)
graph.render('Account',format='png')
修改中文乱码
import re
# 打开 dot_data.dot,修改 fontname="支持的中文字体"
f = open('Account', 'r', encoding='utf-8')
with open('./Account2', 'w', encoding="utf-8") as file:
file.write(re.sub(r'fontname=helvetica', 'fontname=Fangsong', f.read()))
f.close()
# 从文件中加载,展示
graph = graphviz.Source.from_file('./Account2')
graph.render('Account')
2.3、信息熵
-
构建好一颗树,数据变的有顺序了(构建前,一堆数据,杂乱无章;构建一颗,整整齐齐,顺序),用什么度量衡表示,数据是否有顺序:信息熵
-
物理学,热力学第二定律(熵),描述的是封闭系统的混乱程度
-
信息熵,和物理学中熵类似的
-
H ( x ) = − ∑ i = 1 n p ( x ) l o g 2 p ( x ) H(x) = -\sum\limits_{i = 1}^n p(x)log_2p(x) H(x)=−i=1∑np(x)log2p(x)
-
H ( x ) = ∑ i = 1 n p ( x ) l o g 2 1 p ( x ) H(x) = \sum\limits_{i = 1}^n p(x)log_2\frac{1}{p(x)} H(x)=i=1∑np(x)log2p(x)1
2.4、信息增益
信息增益是知道了某个条件后,事件的不确定性下降的程度。写作 g(X,Y)。它的计算方式为熵减去条件熵,如下
g ( X , y ) = H ( Y ) − H ( Y ∣ X ) g(X,y) \rm = H(Y) - H(Y|X) g(X,y)=H(Y)−H(Y∣X)
表示的是,知道了某个条件后,原来事件不确定性降低的幅度。
2.5、手动计算实现决策树分类
数据整合
X['真实用户'] = y
X
计算未划分信息熵
s = X['真实用户']
p = s.value_counts()/s.size
(p * np.log2(1/p)).sum()
按照日志密度进行划分
x = X['日志密度'].unique()
x.sort()
# 如何划分呢,分成两部分
for i in range(len(x) - 1):
split = x[i:i+2].mean()
cond = X['日志密度'] <= split
# 概率分布
p = cond.value_counts()/cond.size
# 按照条件划分,两边的概率分布情况
indexs =p.index
entropy = 0
for index in indexs:
user = X[cond == index]['真实用户']
p_user = user.value_counts()/user.size
entropy += (p_user * np.log2(1/p_user)).sum() * p[index]
print(split,entropy)
筛选最佳划分条件
columns = ['日志密度','好友密度','真实头像']
lower_entropy = 1
condition = {}
for col in columns:
x = X[col].unique()
x.sort()
print(x)
# 如何划分呢,分成两部分
for i in range(len(x) - 1):
split = x[i:i+2].mean()
cond = X[col] <= split
# 概率分布
p = cond.value_counts()/cond.size
# 按照条件划分,两边的概率分布情况
indexs =p.index
entropy = 0
for index in indexs:
user = X[cond == index]['真实用户']
p_user = user.value_counts()/user.size
entropy += (p_user * np.log2(1/p_user)).sum() * p[index]
print(col,split,entropy)
if entropy < lower_entropy:
condition.clear()
lower_entropy = entropy
condition[col] = split
print('最佳列分条件是:',condition)
进一步列分
cond = X['好友密度'] < 0.5
X_ = X[cond]
columns = ['日志密度','真实头像']
lower_entropy = 1
condition = {}
for col in columns:
x = X_[col].unique()
x.sort()
print(x)
# 如何划分呢,分成两部分
for i in range(len(x) - 1):
split = x[i:i+2].mean()
cond = X_[col] <= split
# 概率分布
p = cond.value_counts()/cond.size
# 按照条件划分,两边的概率分布情况
indexs =p.index
entropy = 0
for index in indexs:
user = X_[cond == index]['真实用户']
p_user = user.value_counts()/user.size
entropy += (p_user * np.log2(1/p_user)).sum() * p[index]
print(col,split,entropy)
if entropy < lower_entropy:
condition.clear()
lower_entropy = entropy
condition[col] = split
print('最佳列分条件是:',condition)
3、决策树分裂指标
常用的分裂条件时:
-
信息增益
-
Gini系数
-
信息增益率
-
MSE(回归问题)
3.1、信息熵(ID3)
在信息论里熵叫作信息量,即熵是对不确定性的度量。从控制论的角度来看,应叫不确定性。信息论的创始人香农在其著作《通信的数学理论》中提出了建立在概率统计模型上的信息度量。他把信息定义为“用来消除不确定性的东西”。在信息世界,熵越高,则能传输越多的信息,熵越低,则意味着传输的信息越少。还是举例说明,假设 Dammi 在买衣服的时候有颜色,尺寸,款式以及设计年份四种要求,而 Sara 只有颜色和尺寸的要求,那么在购买衣服这个层面上 Dammi 由于选择更多因而不确定性因素更大,最终 Dammi所获取的信息更多,也就是熵更大。所以信息量=熵=不确定性,通俗易懂。在叙述决策树时我们用熵表示不纯度(Impurity)。
对应公式如下:
H ( x ) = − ∑ i = 1 n p ( x ) l o g 2 p ( x ) H(x) = -\sum\limits_{i = 1}^n p(x)log_2p(x) H(x)=−i=1∑np(x)log2p(x)
熵的变化越大,说明划分越纯,信息增益越大~
3.2、Gini系数(CART)
基尼系数是指国际上通用的、用以衡量一个国家或地区居民收入差距的常用指标。
基尼系数最大为“1”,最小等于“0”。基尼系数越接近 0 表明收入分配越是趋向平等。国际惯例把 0.2 以下视为收入绝对平均,0.2-0.3 视为收入比较平均;0.3-0.4 视为收入相对合理;0.4-0.5 视为收入差距较大,当基尼系数达到 0.5 以上时,则表示收入悬殊。
基尼系数的实际数值只能介于 0~1 之间,基尼系数越小收入分配越平均,基尼系数越大收入分配越不平均。国际上通常把 0.4 作为贫富差距的警戒线,大于这一数值容易出现社会动荡。
Gini 系数越小,代表集合中的数据越纯,所有我们可以计算分裂前的值在按照某个维度对数据集进行划分,然后可以去计算多个节点的 Gini 系数。
对应公式如下:
g i n i = ∑ i = 1 n p i ( 1 − p i ) \rm gini = \sum\limits_{i = 1}^np_i(1 - p_i) gini=i=1∑npi(1−pi)
在对数据进行分类是gini系数的变化越大,说明划分越纯,效果越好~
3.3、信息增益率
大学期末的数学考试只有单选题。对于一个完全没有学习过的学生。该如何过关呢?
4个选项是正确选项的概率都是1/4。那么单项选择题的答案的熵就是:
H ( Y ) = − 0.25 l o g 2 ( 0.25 ) × 4 = 2 b i t H(Y) \rm = -0.25log_2(0.25) \times 4 = 2bit H(Y)=−0.25log2(0.25)×4=2bit
在学霸圈做单项选择题有一个秘籍:三长一短选最短,三短一长选最长。姑且假设学霸的秘籍一般都是正确的。
如果在某场考试中,有10%的单项选题是三长一短,10%的选题是三短一长。计算该考试单项选题的关于长短题的条件熵:
| 题目类型 | 答案概率 | 题目概率 |
|---|---|---|
| 三长一短 | (1,0,0,0)熵是0,结果确定! | 10% |
| 三短一长 | (1,0,0,0)熵是0 | 10% |
| 一样长 | (0.25,0.25,0.25,0.25)熵是2 | 80% |
计算条件熵(条件就是:题目不同类型)
H ( Y ∣ X ) = 0.1 × 0 + 0.1 × 0 + 0.8 × 2 = 1.6 b i t H(Y|X) \rm = 0.1\times 0 + 0.1 \times 0 + 0.8 \times 2 = 1.6bit H(Y∣X)=0.1×0+0.1×0+0.8×2=1.6bit
那么信息增益是:
g ( X , Y ) = H ( Y ) − H ( Y ∣ X ) = 2 − 1.6 = 0.4 b i t g(X,Y) \rm = H(Y) - H(Y|X) = 2 - 1.6 = 0.4bit g(X,Y)=H(Y)−H(Y∣X)=2−1.6=0.4bit
信息增益率在信息增益的基础上增加了惩罚项,惩罚项是特征的固有值。
写作 gr(X,Y)。定义为信息增益除以特征的固有值,如下:
g r ( X , Y ) = g ( X , Y ) I n f o ( X ) gr(X,Y) = \frac{g(X,Y)}{Info(X)} gr(X,Y)=Info(X)g(X,Y)
I n f o ( X ) = − ∑ v ∈ v a l u e s ( X ) n u m ( v ) n u m ( X ) l o g 2 n u m ( v ) n u m ( X ) Info(X) = -\sum\limits_{v \in values(X)}\frac{num(v)}{num(X)}log_2{\frac{num(v)}{num(X)}} Info(X)=−v∈values(X)∑num(X)num(v)log2num(X)num(v)
计算上面单选题题目长短案例的信息增益率:
I n f o ( X ) = − ( 0.1 × l o g 2 0.1 × 2 + 0.8 × l o g 2 0.8 ) = 0.92 Info(X) = -(0.1 \times log_20.1 \times 2 + 0.8 \times log_20.8) = 0.92 Info(X)=−(0.1×log20.1×2+0.8×log20.8)=0.92
g r ( X , Y ) = g ( X , Y ) I n f o ( X ) = 0.4 0.92 = 0.43 gr(X,Y) = \frac{g(X,Y)}{Info(X)} = \frac{0.4}{0.92} = 0.43 gr(X,Y)=Info(X)g(X,Y)=0.920.4=0.43
对于取值多的属性,尤其一些连续型数值,这个单独的属性就可以划分所有的样本,使得所有分支下的样本集合都是“纯的”(最极端的情况是每个叶子节点只有一个样本)。
一个属性的信息增益越大,表明属性对样本的熵减少的能力更强,这个属性使得数据由不确定性变成确定性的能力越强。
所以如果是取值更多的属性,更容易使得数据更“纯”(尤其是连续型数值),其信息增益更大,决策树会首先挑选这个属性作为树的顶点。结果训练出来的形状是一棵庞大且深度很浅的树,这样的划分是极为不合理的。
C4.5使用了信息增益率,在信息增益的基础上除了一项split information,来惩罚值更多的属性。从而使划分更加合理!
3.4、MSE
用于回归树,后面章节具体介绍
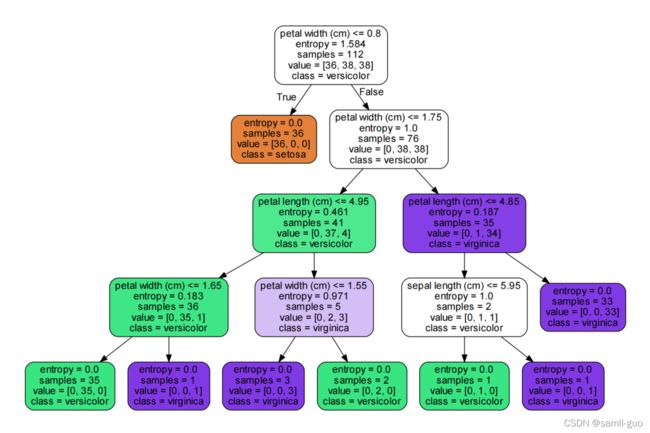
4、鸢尾花分类代码实战
4.1、决策树分类鸢尾花数据集
import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import tree
import matplotlib.pyplot as plt
X,y = datasets.load_iris(return_X_y=True)
# 随机拆分
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 256)
# max_depth调整树深度:剪枝操作
# max_depth默认,深度最大,延伸到将数据完全划分开为止。
model = DecisionTreeClassifier(max_depth=None,criterion='entropy')
model.fit(X_train,y_train)
y_ = model.predict(X_test)
print('真实类别是:',y_test)
print('算法预测是:',y_)
print('准确率是:',model.score(X_test,y_test))
# 决策树提供了predict_proba这个方法,发现这个方法,返回值要么是0,要么是1
model.predict_proba(X_test)
4.2、决策树可视化
import graphviz
from sklearn import tree
# 导出数据
dot_data = tree.export_graphviz(model,feature_names=fn,
class_names=iris['target_names'],# 类别名
filled=True, # 填充颜色
rounded=True,)
graph = graphviz.Source(dot_data)
graph.render('iris')
4.3、决策树剪枝
# 设置图片的尺寸
# 鸢尾花4个属性
iris = datasets.load_iris()
X = iris['data']
y = iris['target']
fn = iris['feature_names']
# 随机拆分
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 256)
# max_depth调整树深度:剪枝操作
# max_depth默认,深度最大,延伸到将数据完全划分开为止。
# min_impurity_decrease(节点划分最小不纯度)如果某节点的不纯度(基尼系数,信息增益,均方差)小于这个阈值,则该节点不再生成子节点
# max_depth(决策树最大深度);min_samples_split(内部节点再划分所需最小样本数)
# min_samples_leaf(叶子节点最少样本数);max_leaf_nodes(最大叶子节点数)
model = DecisionTreeClassifier(criterion='entropy',min_impurity_decrease=0.2)
model.fit(X_train,y_train)
y_ = model.predict(X_test)
print('真实类别是:',y_test)
print('算法预测是:',y_)
print('准确率是:',model.score(X_test,y_test))
# 导出数据
dot_data = tree.export_graphviz(model,feature_names=fn,
class_names=iris['target_names'],# 类别名
filled=True, # 填充颜色
rounded=True,)
graph = graphviz.Source(dot_data)
graph.render('./13-iris-裁剪')
4.4、选择合适的超参数并可视化
import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import tree
import matplotlib.pyplot as plt
X,y = datasets.load_iris(return_X_y=True)
# 随机拆分
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 256)
depth = np.arange(1,16)
err = []
for d in depth:
model = DecisionTreeClassifier(criterion='entropy',max_depth=d)
model.fit(X_train,y_train)
score = model.score(X_test,y_test)
err.append(1 - score)
print('错误率为%0.3f%%' % (100 * (1 - score)))
plt.rcParams['font.family'] = 'STKaiti'
plt.plot(depth,err,'ro-')
plt.xlabel('决策树深度',fontsize = 18)
plt.ylabel('错误率',fontsize = 18)
plt.title('筛选合适决策树深度')
plt.grid()
plt.savefig('./14-筛选超参数.png',dpi = 200)
4.5、决策树副产物
-
特征重要性
model.feature_importances_ -
你想一下逻辑斯蒂回归,是否也有这个属性呢?
it(X_train,y_train)
score = model.score(X_test,y_test)
err.append(1 - score)
print(‘错误率为%0.3f%%’ % (100 * (1 - score)))
plt.rcParams[‘font.family’] = ‘STKaiti’
plt.plot(depth,err,‘ro-’)
plt.xlabel(‘决策树深度’,fontsize = 18)
plt.ylabel(‘错误率’,fontsize = 18)
plt.title(‘筛选合适决策树深度’)
plt.grid()
plt.savefig(’./14-筛选超参数.png’,dpi = 200)
[外链图片转存中...(img-QHJbmSLk-1639204961292)]
#### 4.5、决策树副产物
* 特征重要性
```Python
model.feature_importances_
- 你想一下逻辑斯蒂回归,是否也有这个属性呢?