PRML第二章读书笔记——Probability Distribution 两变量条件期望/方差、R-M序列算法、高斯分布参数辨识/后验推断/相关分布、指数族分布、无参数先验、无参数估计、kNN
第2章 Probability Distribution
- 2.2 Multinomial Variables
-
-
- P74 两变量的条件期望与条件方差
-
- 2.3 The Gaussian Distribution
-
-
- P86 高斯分布的参数辨识
- P94 序列估计
-
-
- Robbins-Monro 算法
-
- P99 高斯分布参数的贝叶斯估计
-
-
- 一般性序列估计
- 一维高斯分布均值的后验推断
- 一维高斯分布方差的后验推断 Gamma分布
- 一维高斯分布均值和方差联合的后验推断 Gaussian-gamma分布
- 高维高斯分布均值的后验推断
- 高维高斯分布方差的后验推断 Wishart分布
- 高维高斯分布均值和方差联合的后验推断 Gaussian-Wishart分布
-
- P103 学生t分布
- P107 von Mises 分布
-
- 2.4 The Exponential Family
-
-
- P113 一般形式
- P115 参数估计与充分统计量
- P117 共轭先验
- P117 无信息先验
-
-
- 尺度参数的无信息先验分布
-
-
- 2.5 无参数概率密度估计
-
-
- P122 核密度估计和近邻方法
- P125 kNN算法的一种无参解释
-
2.2 Multinomial Variables
P74 两变量的条件期望与条件方差
由Exercise2.8:考虑两个变量 x x x和 y y y,联合概率分布为 p ( x , y ) p(x,y) p(x,y). 那么
E [ x ] = E y [ E x [ x ∣ y ] ] , 这条较为广知 v a r [ x ] = E y [ v a r x [ x ∣ y ] ] + v a r y [ E x [ x ∣ y ] ] . \mathbb{E}[x]=\mathbb{E}_y [\mathbb{E}_x[x|y]], \text{ 这条较为广知} \\ var[x]=\mathbb{E}_y[var_x[x|y]]+var_y[\mathbb{E}_x[x|y]]. E[x]=Ey[Ex[x∣y]], 这条较为广知var[x]=Ey[varx[x∣y]]+vary[Ex[x∣y]].
这里 E x [ x ∣ y ] \mathbb{E}_x[x|y] Ex[x∣y]表示在条件分布 p ( x ∣ y ) p(x|y) p(x∣y)下, x x x的期望。条件方差记号类似。
所以可知
E θ [ θ ] = E D [ E θ [ θ ∣ D ] ] v a r θ [ θ ] = E D [ v a r θ [ θ ∣ D ] ] + v a r D [ E θ [ θ ∣ D ] ] \mathbb{E}_\theta[\theta]=\mathbb{E}_\mathcal{D} [\mathbb E_\theta[\theta|\mathcal D]] \\ var_\theta [\theta] = \mathbb E_\mathcal D [var_\theta [\theta | \mathcal D]] + var_\mathcal D [\mathbb E _\theta [\theta | \mathcal D]] Eθ[θ]=ED[Eθ[θ∣D]]varθ[θ]=ED[varθ[θ∣D]]+varD[Eθ[θ∣D]]
注意二式的右侧,第一项为 θ \theta θ的后验分布方差的期望,第二项为后验分布期望的方差。
其中, v a r D [ E θ [ θ ∣ D ] ] > 0 var_\mathcal D [\mathbb E _\theta [\theta | \mathcal D]] > 0 varD[Eθ[θ∣D]]>0,所以 v a r θ [ θ ] > E D [ v a r θ [ θ ∣ D ] ] var_\theta [\theta] > \mathbb E_\mathcal D [var_\theta [\theta | \mathcal D]] varθ[θ]>ED[varθ[θ∣D]]。也就是说观测到数据后, θ \theta θ的不确定性会减小。不过这只对平均而言成立。可以构造特殊的数据集,并让 θ \theta θ的后验分布的方差变大。
(疑问:这好像并不能证明 c a r d [ D ] card[\mathcal D] card[D]越大,不确定性越小。这里猜测可以用类似方法证明,写出两个数据集 D 1 \mathcal D_1 D1和 D 2 \mathcal D_2 D2, D 1 \mathcal D_1 D1放到两侧, D 2 \mathcal D_2 D2放到右边,构造一个类似上述的式子?有空试一波!)
2.3 The Gaussian Distribution
P86 高斯分布的参数辨识
高斯分布在给定形式后,如何看出参数 μ \mu μ和方差 Σ \Sigma Σ,直接关注指数表达式即可:
− 1 2 ( x − μ ) T Σ − 1 ( x − μ ) = − 1 2 x T Σ − 1 x + x T Σ − 1 μ + c o n s t -\frac{1}{2}(x-\mu)^T \Sigma^{-1} (x - \mu) = -\frac{1}{2}x^T \Sigma^{-1}x + x^T\Sigma^{-1}\mu+const −21(x−μ)TΣ−1(x−μ)=−21xTΣ−1x+xTΣ−1μ+const
只要写成这样的形式,就能直接从二次项中读出 1 2 Σ − 1 \frac{1}{2}\Sigma^{-1} 21Σ−1,从一次项读出 Σ − 1 μ \Sigma^{-1}\mu Σ−1μ.
用这样的方法,2.3.1节写出当全变量为高斯分布时的条件分布
2.3.2节给出了边缘分布
2.3.3节给出了线性高斯模型的边缘分布和条件分布,即
x ∼ N ( x ∣ μ , Λ − 1 ) y ∣ x ∼ N ( y ∣ A x + b , L − 1 ) \begin{aligned} x &\sim \mathcal{N}(x|\mu, \Lambda^{-1}) \\ y|x &\sim \mathcal{N}(y|Ax+b, L^{-1}) \end{aligned} xy∣x∼N(x∣μ,Λ−1)∼N(y∣Ax+b,L−1)其中 Λ = Σ − 1 \Lambda=\Sigma^{-1} Λ=Σ−1被称为精度矩阵Precision Matrix)
线性高斯模型的结果 y y y仍然是高斯分布
E [ y ] = A μ + b c o v [ y ] = L − 1 + A Λ − 1 A T \begin{aligned} \mathbb E[y] &=A\mu+b \\ cov[y] &=L^{-1}+A\Lambda^{-1}A^T \end{aligned} E[y]cov[y]=Aμ+b=L−1+AΛ−1AT
P94 序列估计
假定样本是一个一个序列观测的,记第 N N N次观测后,均值估计为 μ M L ( N ) \mu_{ML}^{(N)} μML(N),则易知
μ M L ( N ) = 1 N ∑ n = 1 N x n = μ M L ( N − 1 ) + 1 N ( x N − μ M L ( N − 1 ) ) \mu_{ML}^{(N)} = \frac{1}{N}\sum_{n=1}^N x_n = \mu_{ML}^{(N-1)} + \frac{1}{N}(x_N - \mu_{ML}^{(N-1)}) μML(N)=N1n=1∑Nxn=μML(N−1)+N1(xN−μML(N−1))
上式可看作是对 μ \mu μ的不断修正。这里考虑一个一般化的序列学习算法:
Robbins-Monro 算法
对于一对随机变量 θ \theta θ和 z z z,并假定 f ( θ ) = E [ z ∣ θ ] f(\theta)= \mathbb E[z|\theta] f(θ)=E[z∣θ]. 希望通过序列数据找到根 θ ∗ \theta^* θ∗满足 f ( θ ∗ ) = 0 f(\theta ^*)=0 f(θ∗)=0.
假定 z z z的条件方差有限,即 E [ ( z − f ) 2 ∣ θ ] < ∞ \mathbb E[(z-f)^2|\theta] < \infty E[(z−f)2∣θ]<∞. 不失一般性,我们认为 θ > θ ∗ \theta > \theta^* θ>θ∗时, f ( θ ) > 0 f(\theta) > 0 f(θ)>0; θ < θ ∗ \theta < \theta^* θ<θ∗时, f ( θ ) < 0 f(\theta) < 0 f(θ)<0. 则
![]()
其中 z ( θ N ) z(\theta^{N}) z(θN)是给定 θ N \theta^N θN下 z z z的观测。
{ α N } \{\alpha _N\} {αN}表示正数序列满足
lim N → ∞ α N = 0 ∑ N = 1 ∞ α N = ∞ ∑ N = 1 ∞ α N 2 < ∞ \lim_{N\rightarrow \infty} \alpha_N = 0 \\ \sum_{N=1}^\infty \alpha_N = \infty \\ \sum_{N=1}^\infty \alpha_N^2 < \infty N→∞limαN=0N=1∑∞αN=∞N=1∑∞αN2<∞
上式会以概率为1收敛到根。 第一项确保了修正项会收敛到一个有限值,第二项确保了不会对根欠收敛,第三项确保了累积噪声的方差有限,所以不会破坏收敛。(这个算法在强化学习的摇臂赌博机中也用到了)
考虑一般的最大似然问题,参数 θ M L \theta_{ML} θML是一个驻点,满足
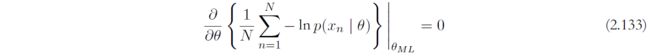
当 N → ∞ N \rightarrow \infty N→∞,上式即
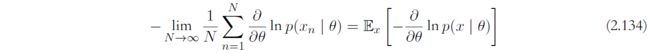
注意这个形式,和Robbins-Monro的要求是一样的,可以得到
![]()
z z z可以看作是其中的 − ∂ ∂ θ ( N − 1 ) ln p ( x N ∣ θ ( N − 1 ) ) -\frac{\partial}{\partial \theta^{(N-1)}}\ln p(x_N| \theta^{(N-1)}) −∂θ(N−1)∂lnp(xN∣θ(N−1))。
对于高斯分布的均值估计 μ M L ( N ) \mu_{ML}^{(N)} μML(N),即 z = − 1 σ 2 ( x − μ M L ) z=-\frac{1}{\sigma^2}(x - \mu_{ML}) z=−σ21(x−μML),取 α N = σ 2 N \alpha_N=\frac{\sigma^2}{N} αN=Nσ2,则得到一致的更新公式。

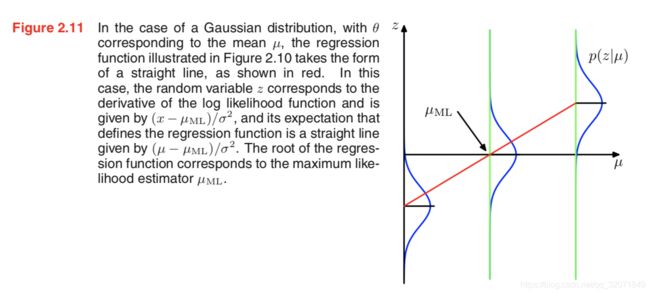
P99 高斯分布参数的贝叶斯估计
一般性序列估计
p ( μ ∣ D ) ∝ [ p ( μ ) ∏ n = 1 N − 1 p ( x n ∣ μ ) ] p ( x N ∣ μ ) p(\mu|D) \propto \left[ p(\mu) \prod_{n=1}^{N-1}p(x_n|\mu) \right] p(x_N|\mu) p(μ∣D)∝[p(μ)n=1∏N−1p(xn∣μ)]p(xN∣μ)
上式括号中的项可以看作是读入到第 N − 1 N-1 N−1个数据之后,得到的参数分布,可以看作是第 N N N次的先验分布。
一维高斯分布均值的后验推断
如果已知方差,不知道均值,假定 μ ∼ N ( μ ∣ μ 0 , σ 0 2 ) \mu \sim \mathcal{N} (\mu|\mu_0, \sigma_0^2) μ∼N(μ∣μ0,σ02), x ∣ μ ∼ N ( x ∣ μ , σ ) x|\mu \sim \mathcal{N} (x|\mu,\sigma) x∣μ∼N(x∣μ,σ),那么由
p ( μ ∣ X ) ∝ p ( X ∣ μ ) p ( μ ) p(\mu|X) \propto p(X|\mu) p(\mu) p(μ∣X)∝p(X∣μ)p(μ)
可得 p ( μ ∣ X ) = N ( μ ∣ μ N , σ N 2 ) p(\mu|X) = \mathcal {N} (\mu|\mu_N, \sigma^2_N) p(μ∣X)=N(μ∣μN,σN2),其中
μ N = σ 2 N σ 0 2 + σ 2 μ 0 + N σ 0 2 N σ 0 2 + σ 2 μ M L 1 σ N 2 = 1 σ 0 2 + N σ 2 \begin{aligned} \mu_N &= \frac{\sigma^2}{N\sigma_0^2+\sigma^2}\mu_0 + \frac{N \sigma_0^2}{N\sigma^2_0+\sigma^2}\mu_{ML} \\ \frac{1}{\sigma^2_N} &=\frac{1}{\sigma_0^2} + \frac{N}{\sigma^2} \end{aligned} μNσN21=Nσ02+σ2σ2μ0+Nσ02+σ2Nσ02μML=σ021+σ2N
N N N是 X X X中样本数, μ M L = 1 N ∑ n = 1 N x n \mu_{ML}=\frac{1}{N}\sum_{n=1}^N x_n μML=N1∑n=1Nxn.
这个式子很有趣
- 当 N = 0 N=0 N=0时,等同于先验分布
- 当 N = ∞ N=\infty N=∞时,等同于极大似然
- 随着 N N N增大时,方差越来越小, μ \mu μ越来越确定
- 当 σ 0 2 = ∞ \sigma^2_0=\infty σ02=∞时,等同于最大似然,方差很大意味着先验没有提供什么稳定的信息
一维高斯分布方差的后验推断 Gamma分布
如果已知均值,不知道方差,采用精确度 λ = 1 σ 2 \lambda=\frac{1}{\sigma^2} λ=σ21进行表示。高斯分布的方差后验为:
p ( X ∣ λ ) = ∏ n = 1 N N ( x n ∣ μ , λ − 1 ) ∝ λ N / 2 e x p { − λ 2 ∑ n = 1 N ( x n − μ ) 2 } p(X|\lambda) = \prod_{n=1}^N \mathcal {N} (x_n| \mu, \lambda^{-1}) \propto \lambda^{N/2} exp \left\{ - \frac{\lambda}{2} \sum_{n=1}^N (x_n - \mu)^2 \right\} p(X∣λ)=n=1∏NN(xn∣μ,λ−1)∝λN/2exp{−2λn=1∑N(xn−μ)2}
注意,这种写法下,对应的先验共轭分布其实是Gamma分布!
G a m ( λ ∣ a , b ) = 1 Γ ( a ) b a λ a − 1 e x p ( − b λ ) Gam(\lambda |a,b) = \frac{1}{\Gamma(a)}b^a \lambda^{a-1} exp(-b\lambda) Gam(λ∣a,b)=Γ(a)1baλa−1exp(−bλ)
如果记先验为 G a m ( λ ∣ a 0 , b 0 ) Gam(\lambda|a_0, b_0) Gam(λ∣a0,b0),则对应的后验为
p ( λ ∣ X ) ∝ λ a 0 − 1 λ N / 2 e x p { − b 0 λ − λ 2 ∑ n = 1 N ( x n − μ ) 2 } p(\lambda|X) \propto \lambda^{a_0 - 1} \lambda^{N/2} exp \left \{ -b_0 \lambda - \frac{\lambda}{2} \sum_{n=1}^{N}(x_n - \mu)^2 \right \} p(λ∣X)∝λa0−1λN/2exp{−b0λ−2λn=1∑N(xn−μ)2}
从中可以辨识出分布为 G a m ( λ ∣ a N , b N ) Gam(\lambda| a_N, b_N) Gam(λ∣aN,bN)
a N = a 0 + N 2 b N = b 0 + 1 2 ∑ n = 1 N ( x n − μ ) 2 = b 0 + N 2 σ M L 2 \begin{aligned} a_N &= a_0 + \frac{N}{2} \\ b_N &= b_0 + \frac{1}{2}\sum_{n=1}^N (x_n - \mu)^2=b_0 + \frac{N}{2} \sigma^2_{ML} \end{aligned} aNbN=a0+2N=b0+21n=1∑N(xn−μ)2=b0+2NσML2
- 当 N N N增大时, a N a_N aN增大,实际上,可以把 a 0 a_0 a0解释成是已经有了的 2 a 0 2a_0 2a0个先验伪观测, b 0 b_0 b0解释成是这 2 a 0 2a_0 2a0个先验观测具有方差 b 0 a 0 \frac{b_0}{a_0} a0b0
- 如果直接估计 σ 2 \sigma^2 σ2,而不是 λ \lambda λ,那么得到对应先验分布是Inverse Gamma 分布。
一维高斯分布均值和方差联合的后验推断 Gaussian-gamma分布
如果方差和均值都不知道,那么 p ( X ∣ μ , λ ) p(X|\mu,\lambda) p(X∣μ,λ)的连乘可以写成如下形式:
p ( μ ∣ λ ) p ( λ ) ∝ N ( μ ∣ μ 0 , ( β λ ) − 1 ) G a m ( λ ∣ a , b ) p(\mu|\lambda)p(\lambda) \propto \mathcal{N} (\mu|\mu_0, (\beta \lambda)^{-1})Gam(\lambda|a, b) p(μ∣λ)p(λ)∝N(μ∣μ0,(βλ)−1)Gam(λ∣a,b)
这也即共轭先验的形式,该分布叫做normal-gamma或Gaussian-gamma分布
高维高斯分布均值的后验推断
如果已知方差,不知道均值,这种情况下,均值仍然是高斯分布。
高维高斯分布方差的后验推断 Wishart分布
如果已知均值,不知道方差,如果记精确度矩阵 Λ = Σ − 1 \Lambda = \Sigma^{-1} Λ=Σ−1,那么共轭先验分布为Wishart分布,这种分布可以看作是Gamma分布的高维推广,就类似于Beta分布和Dirichlet分布的关系。表达式为
W ( Λ ∣ W , ν ) = B ∣ Λ ∣ ( ν − D − 1 ) / 2 e x p { − 1 2 T r ( W − 1 Λ ) } \mathcal{W} (\Lambda|W, \nu) = B|\Lambda|^{(\nu - D - 1) / 2}exp\left \{ -\frac{1}{2}Tr(W^{-1}\Lambda) \right\} W(Λ∣W,ν)=B∣Λ∣(ν−D−1)/2exp{−21Tr(W−1Λ)}
其中 ν \nu ν是自由度, B B B为归一化因子
B ( W , ν ) = ∣ W ∣ − ν / 2 ( 2 ν D / 2 π D ( D − 1 ) / 4 ∏ i = 1 D Γ ( ν + 1 − i 2 ) ) − 1 B(W, \nu) = |W|^{-\nu / 2} \left(2^{\nu D / 2} \pi ^{D(D-1)/4} \prod_{i=1}^{D} \Gamma (\frac{\nu + 1 - i} {2}) \right) ^{-1} B(W,ν)=∣W∣−ν/2(2νD/2πD(D−1)/4i=1∏DΓ(2ν+1−i))−1
如果直接对 Σ \Sigma Σ估计,而不是 Λ \Lambda Λ,则得到对应的共轭先验为Inverse Wishart分布
高维高斯分布均值和方差联合的后验推断 Gaussian-Wishart分布
如果方差和均值都不知道,那么共轭先验的形式为:
p ( μ , Λ ∣ μ 0 , β , W , ν ) = N ( μ ∣ μ 0 , ( β Λ ) − 1 ) W ( Λ ∣ W , ν ) p(\mu, \Lambda| \mu_0, \beta, W, \nu) = \mathcal {N} (\mu| \mu_0, (\beta\Lambda)^{-1}) \mathcal{W} (\Lambda|W, \nu) p(μ,Λ∣μ0,β,W,ν)=N(μ∣μ0,(βΛ)−1)W(Λ∣W,ν)
称之为Normal-Wishart或Gaussian-Wishart分布。
P103 学生t分布
如果一维高斯分布精确度先验为Gamma分布,均值已知,则 x x x的边缘分布为
p ( x ∣ μ , a , b ) = ∫ 0 ∞ N ( x ∣ μ , τ − 1 ) G a m ( τ ∣ a , b ) d τ = b a Γ ( a ) ( 1 2 π ) 1 / 2 [ b + ( x − μ ) 2 2 ] − a − 1 / 2 Γ ( a + 1 / 2 ) \begin{aligned} p(x|\mu, a,b ) &= \int_0^{\infty}\mathcal {N} (x | \mu, \tau^{-1})Gam(\tau|a,b)d\tau \\ &=\frac{b^a}{\Gamma(a)}\left(\frac{1}{2\pi}\right)^{1/2} \left [b+\frac{(x-\mu)^2}{2}\right]^{-a-1/2}\Gamma(a+1/2) \end{aligned} p(x∣μ,a,b)=∫0∞N(x∣μ,τ−1)Gam(τ∣a,b)dτ=Γ(a)ba(2π1)1/2[b+2(x−μ)2]−a−1/2Γ(a+1/2)
如果记 ν = 2 a , λ = a / b \nu=2a, \lambda=a/b ν=2a,λ=a/b,则上式化学生t分布
S t ( x ∣ μ , λ , ν ) = Γ ( ν / 2 + 1 / 2 ) Γ ( ν / 2 ) ( λ π ν ) 1 / 2 [ 1 + λ ( x − μ ) 2 ν ] − ν / 2 − 1 / 2 St(x|\mu, \lambda, \nu) = \frac{\Gamma(\nu/2 + 1/2)}{\Gamma(\nu/2)} \left( \frac{\lambda}{\pi \nu}\right)^{1/2} \left[1+\frac{\lambda(x-\mu)^2}{\nu}\right] ^{-\nu/2 - 1/2} St(x∣μ,λ,ν)=Γ(ν/2)Γ(ν/2+1/2)(πνλ)1/2[1+νλ(x−μ)2]−ν/2−1/2
λ \lambda λ有时称为t分布的precision, ν \nu ν称为自由度。 ν = 1 \nu=1 ν=1时,退化为Cauchy distribution; ν → ∞ \nu \rightarrow \infty ν→∞时,成为高斯分布 N ( x ∣ μ , λ − 1 ) \mathcal{N} (x| \mu, \lambda^{-1}) N(x∣μ,λ−1).

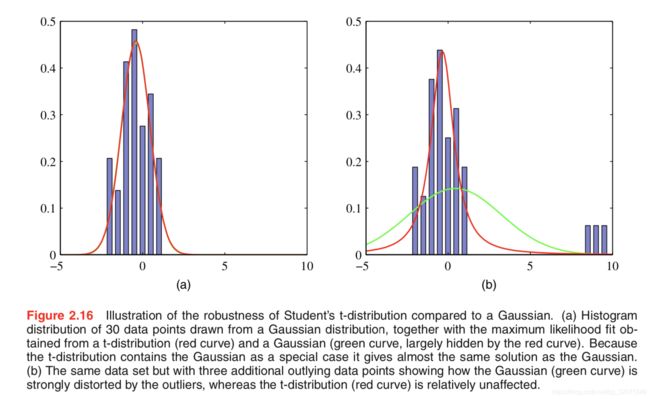
- 相比于高斯分布,学生t分布的一个优点抗离群点robust,学生t分布的尾巴比较厚,没有高斯分布那么敏感。另外,如果一组数据,高斯分布拟合得好,学生t分也能拟合好,因为高斯分布是学生t分布的一个特例。如图所示
如果再另 η = τ b / a \eta=\tau b/a η=τb/a,则学生t分布又可写为
S t ( x ∣ μ , λ , ν ) = ∫ 0 ∞ N ( x ∣ μ , ( η λ ) − 1 ) G a m ( η ∣ ν / 2 , ν / 2 ) d η St(x|\mu, \lambda, \nu)=\int _0^\infty \mathcal{N} (x|\mu, (\eta \lambda)^{-1})Gam(\eta| \nu/2, \nu/2)d\eta St(x∣μ,λ,ν)=∫0∞N(x∣μ,(ηλ)−1)Gam(η∣ν/2,ν/2)dη
通过该形式,可以扩展出高维学生t分布
S t ( x ∣ μ , Λ , ν ) = ∫ 0 ∞ N ( x ∣ μ , ( η Λ ) − 1 ) G a m ( η ∣ ν / 2 , ν / 2 ) d η = Γ ( ν / 2 + D / 2 ) Γ ( ν / 2 ) ∣ Λ ∣ 1 / 2 ( π ν ) D / 2 [ 1 + Δ 2 ν ] − ν / 2 − D / 2 \begin{aligned} St( x|\mu, \Lambda, \nu) &=\int _0^\infty \mathcal{N} (x|\mu, (\eta \Lambda)^{-1})Gam(\eta| \nu/2, \nu/2)d\eta \\ &= \frac{\Gamma(\nu/2 + D/2)}{\Gamma(\nu/2)} \frac{|\Lambda|^{1/2}}{(\pi \nu) ^{D/2}} \left[1+\frac{\Delta^2}{\nu}\right] ^{-\nu/2 - D/2} \end{aligned} St(x∣μ,Λ,ν)=∫0∞N(x∣μ,(ηΛ)−1)Gam(η∣ν/2,ν/2)dη=Γ(ν/2)Γ(ν/2+D/2)(πν)D/2∣Λ∣1/2[1+νΔ2]−ν/2−D/2
其中 D D D是维度, Δ 2 = ( x − μ ) T Λ ( x − μ ) \Delta^2=(x-\mu)^T\Lambda(x-\mu) Δ2=(x−μ)TΛ(x−μ)
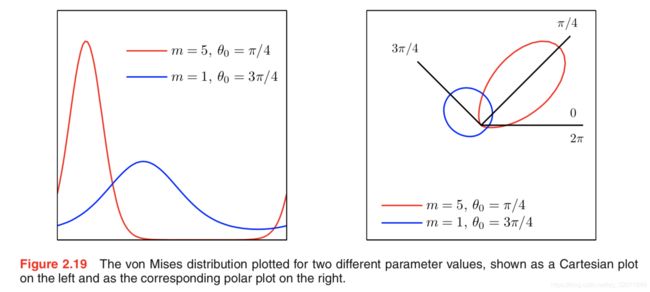
P107 von Mises 分布
一个二维高斯分布,关注其在以原点为圆心的单位圆下的条件概率分布,角度的分布为von Mises分布(循环正态分布)
p ( θ ∣ θ 0 , m ) = 1 2 π I 0 ( m ) e x p { m c o s ( θ − θ 0 ) } p(\theta|\theta_0, m)=\frac{1}{2\pi I_0(m)} exp\{ m cos(\theta - \theta_0)\} p(θ∣θ0,m)=2πI0(m)1exp{mcos(θ−θ0)}
其中 m = r 0 / σ 2 , r 0 = ∥ μ ∥ 2 , θ 0 = t a n − 1 ( μ y / μ x ) m = r_0/\sigma^2, r_0 = \left \| \mu \right \|_2,\theta_0=tan^{-1}(\mu_y/\mu_x) m=r0/σ2,r0=∥μ∥2,θ0=tan−1(μy/μx),而
I 0 ( m ) = 1 2 π ∫ 0 2 π e x p { m c o s θ } d θ I_0(m)=\frac{1}{2\pi} \int _0^{2\pi} exp \{m cos\theta\} d\theta I0(m)=2π1∫02πexp{mcosθ}dθ
是归一化因子。
- 当 m m m变大时,von Mises分布近似高斯分布
2.4 The Exponential Family
P113 一般形式
p ( x ∣ η ) = h ( x ) g ( η ) e x p { η T u ( x ) } p(x|\eta) = h(x)g(\eta)exp\{ \eta^T u(x)\} p(x∣η)=h(x)g(η)exp{ηTu(x)}
其中 x x x可以是一维或多维,也可以是离散或连续。 g ( η ) g(\eta) g(η)叫做natural parameters,可看作归一化因子
实际上,本章中上述讨论过的概率分布都是指数族分布的特例。
P115 参数估计与充分统计量
考虑一般参数 η \eta η估计问题,最大似然得到
p ( X ∣ η ) ∝ g ( η ) N e x p { η T ∑ n = 1 N u ( x n ) } p(X|\eta) \propto g(\eta)^Nexp \left\{ \eta^T \sum_{n=1}^N u(x_n) \right\} p(X∣η)∝g(η)Nexp{ηTn=1∑Nu(xn)}
对数求导后得到
− ∇ ln g ( η M L ) = 1 N ∑ n = 1 N u ( x n ) -\nabla \ln g(\eta_{ML}) = \frac{1}{N}\sum_{n=1}^N u(x_n) −∇lng(ηML)=N1n=1∑Nu(xn)
- 注意这里 ∑ n u ( x n ) \sum_n u(x_n) ∑nu(xn)足够计算 η \eta η,所以被称为充分统计量。例如对于Bernoulli分布,仅需要保存 { x n } \{x_n\} {xn}的和,对于高斯分布,需要保存 { x n } , { x n 2 } \{x_n\}, \{x_n^2\} {xn},{xn2}各自的和。
- 当 N → ∞ N \rightarrow \infty N→∞时,右侧变为 E x [ u ( x ) ] \mathbb E _x[u(x)] Ex[u(x)].
P117 共轭先验
p ( η ∣ χ , ν ) = f ( χ , ν ) g ( η ) ν e x p { ν η T χ } p(\bm {\eta}| \bm \chi, \nu) = f(\bm\chi ,\nu)g(\bm\eta)^\nu exp\{ \nu \bm\eta^T\bm \chi\} p(η∣χ,ν)=f(χ,ν)g(η)νexp{νηTχ}
其中 f f f是一个归一化因子, g g g和 p ( X ∣ η ) p(X|\eta) p(X∣η)中形式一样。易得后验
p ( η ∣ X , χ , ν ) ∝ g ( η ) ν + N e x p { η T ( ∑ n = 1 N u ( x n ) + ν χ ) } p(\eta |\bf X, \bf \chi, \nu) \propto g(\eta)^{\nu + N} exp \left\{ \eta^T \left ( \sum_{n=1}^N \bf u(\bf x_n) + \nu \bf \chi \right )\right \} p(η∣X,χ,ν)∝g(η)ν+Nexp{ηT(n=1∑Nu(xn)+νχ)}
其中 ν \nu ν被看作是先验伪观测数,每一次观测的统计量 u ( x ) u(x) u(x)为 χ \chi χ
P117 无信息先验
无信息先验这个东西稍微抽象,偏贝叶斯思维。解决的问题是在无先验时如何选择先验,选择的思想是先验要对后验的影响最小。
如果没有什么信息,我们假定先验是均匀分布,这么做存在两个困难:
- 在无限连续数域上发散。称之为反常先验分布。但如果后验分布是正常的,那么可以使用这样的分布(称之为广义先验分布)。例如高斯分布,如果假定均值先验是均匀分布,只要观测到一个数据点,那么后验就正常。
- 如果另一个参数是该参数的非线性变换,那么将不再是均匀分布
(可以参考下这篇博客:感觉写得很好!https://blog.csdn.net/weixin_41929524/article/details/80674219)
尺度参数的无信息先验分布
如果一个分布形式为
p ( x ∣ σ ) = 1 σ f ( x σ ) p(x|\sigma) = \frac{1}{\sigma} f (\frac{x}{\sigma}) p(x∣σ)=σ1f(σx)
其中 σ > 0 \sigma > 0 σ>0, f ( x ) f(x) f(x)已经归一化。
考虑 y = c x , η = c σ y=cx, \eta = c\sigma y=cx,η=cσ其中 c > 0 c> 0 c>0. 那么
p ( y ∣ η ) = 1 η f ( y η ) p(y|\eta) = \frac{1}{\eta} f (\frac{y}{\eta}) p(y∣η)=η1f(ηy)
x x x和 y y y的函数形式相同,所以 η \eta η和 σ \sigma σ应该有相同的先验分布,如果 σ \sigma σ的先验分布为 π σ ( σ ) \pi_\sigma(\sigma) πσ(σ),那么
π η ( η ) = π σ ( σ ) ∣ d σ d η ∣ = 1 c π σ ( η c ) π η = π σ \begin{aligned} \pi_\eta(\eta) &= \pi_\sigma(\sigma) \left |\frac{d\sigma}{d\eta} \right|=\frac{1}{c}\pi_{\sigma} (\frac{\eta}{c}) \\ \pi_\eta &=\pi_\sigma \end{aligned} πη(η)πη=πσ(σ)∣∣∣∣dηdσ∣∣∣∣=c1πσ(cη)=πσ
取 η = c \eta=c η=c,解得 π η ( η ) = π η ( 1 ) η \pi_\eta(\eta)=\frac{\pi_\eta(1)}{\eta} πη(η)=ηπη(1),取 π η ( 1 ) = 1 \pi_\eta(1)=1 πη(1)=1,则先验分布为 1 / η 1/\eta 1/η.
这样的一个例子是高斯分布中的标准差
p ( x ∣ σ ) = σ − 1 e x p { − ( x σ ) 2 } p(x|\sigma) = \sigma^{-1}exp \left \{ -\left (\frac{x}{\sigma} \right )^{2} \right \} p(x∣σ)=σ−1exp{−(σx)2}
还有一种位置参数的无信息先验分布,可以看原书,推导出的结果是均匀分布。
2.5 无参数概率密度估计
P122 核密度估计和近邻方法
这种估计方法不明确给出概率分布的表达式,而是通过数据进行感知。柱状图其实就是一种无参数的概率密度估计方法。
另外一种常用的 p ( x ) p(x) p(x)估计方法是观察 x x x的小邻域。记 N N N为总样本数, K K K为小邻域内样本数,如果小邻域足够小,认为小邻域内概率不变,则有
p ( x ) = K N V p(x) = \frac{K}{NV} p(x)=NVK
这里如果固定 V V V,则该方法为核密度估计;如果固定 N N N,则为近邻估计,即找以 x x x为中心包含 K K K个点的最小超球,当作 V V V.
P125 kNN算法的一种无参解释
在近邻方法当中,如果有多个类,则对于第 C k \mathcal C_k Ck类,记样本数为 N k N_k Nk,小邻域内有样本数 K k K_k Kk,则
p ( x ∣ C k ) = K k N k V p ( x ) = K N V p ( C k ) = N k N \begin{aligned} \\ p(x|\mathcal C_k) &= \frac{K_k}{N_kV} \\ p(x) &=\frac{K}{NV} \\ p(\mathcal C_k) &= \frac{N_k}{N} \end{aligned} p(x∣Ck)p(x)p(Ck)=NkVKk=NVK=NNk
则后验为
p ( C k ∣ x ) = p ( x ∣ C k ) p ( C k ) p ( x ) = K k K p(\mathcal C_k|x) = \frac{p(x|\mathcal C_k)p(C_k)}{p(x)} = \frac{K_k}{K} p(Ck∣x)=p(x)p(x∣Ck)p(Ck)=KKk
这样,kNN分类就可以解释为是近邻方法中,后验概率最大的类别。
- 1-NN分类器有一个很有趣的性质:当 N → ∞ N \rightarrow \infty N→∞时,分类错误率不会超过贝叶斯最优分类器错误率的两倍
- 最优分类器可以理解为是看到了真实后验分布
- (我记得这个性质是要求概率连续的)
- 可以参考西瓜书P226
参考文献:
[1] Christopher M. Bishop. Pattern Recognition and Machine Learning. 2006