第五次周报10.23

摘要

本周继续研究卷积神经网络，主要解决清楚了卷积的数学性质和物理意义以及相关问题，以及阅读了《Striving for Simplicity: The All Convolutional Net》，这篇文献围绕着“池化层可否被替代”进行讨论。通过这些学习，对卷积神经网络的了解更深刻了。

卷积

什么是卷积？

顾名思义，卷积主要有两个操作，一个是“卷”，一个是“积”，想要更好的理解这两个操作，要从它的公式开始

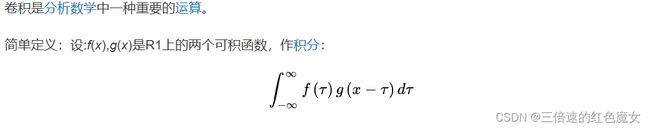
通过图片可知，卷积就是一种运算，但看着还是很抽象，你积分跟我卷积有啥关系？
下面来举个例子：
考虑一个问题：
有个人24小时都在吃东西，f(t)代表他在t时刻进食了多少，g(t)代表食物消化的比率，问在他吃了12小时后，他肚子里还剩多少食物？

从图上看到，计算肚子里食物的量，不可以简单粗暴的直接把 过去吃的食物都相加，还要考虑”消化的问题“。以大米饭为例子，假设他在2点吃了大米饭，在4点时，大米饭剩下的量就是 f(2)g(4-2)
大米饭只是一样食物，要求他在4点时，肚子里的食物存量，就把4点前吃的各个食物考虑进去了，也就是求积分了，任意t时刻，求肚子里食物的存量，更标准的公式如下：

看到这里，跟卷积公式对比，除了上下限不同，积分变量符号不同（符号可以换，上下限也可以换，只不过这里把时间作为上下限，有具体的物理意义，不能作为∞）其他的都一毛一样。

两个问题解决了一个”积“，那”卷“体现在哪里了呢？
回到刚刚的系统，求在T时刻肚子里的存量，那在T时刻吃的东西，剩余食物的比率是最高的，越早吃的食物，剩余食物的比率就越低，对应的点的关系，图像如下：

看着是不是很别扭，翻转过来~

你应该知道了，每条线都是一对f与g相乘，只不过翻转过来，才是它们真正的对应关系，卷积的结果就是：翻转过来之后的对应的每一对f与g相乘再相加。

什么时候需要卷积？

通过以上的例子，我们可知：若一个系统的输入是不稳定的，输出是稳定的，就可以通过卷积求系统的存量（每个输入都会影响到最后的输出且影响程度不一样）

比如：蝴蝶效应，银行存钱若干年后能拿多少钱（本金，利息对输出结果都有叠加影响）

讲到这里，终于说完了卷积公式的意义，下面开始阐述 图像的卷积操作

什么是图像的卷积操作？

解决这个问题，也要考虑什么是”卷“，什么是”积“

应用到图像的”积“操作，就不用多说了，图像对应卷积核相乘再相加。
这里大家可能会有个疑惑，为什么上面的卷积公式中的积，是求积分，这里变成了乘积？ 我也不知道为啥…可能卷积在每个领域应用都会有形式上的变化吧？但总体含义是不变的，比如在图像识别领域，每个像素点都是离散的，就不能用积分了，卷积变成这样的点乘操作更能满足需求，当然这些都是我不严谨的解释，再问就是满足”自洽性“。

那对图像的卷积操作中，它是怎么”卷“的？它为什么要”卷“？
想要说清楚这两个问题，还得解释卷积核干了什么，我们都知道，不同的数值的卷积核对图像进行处理，处理后的结果也不一样，下列都3x3数值为1/9的卷积核，就是对图像进行了 平滑 操作

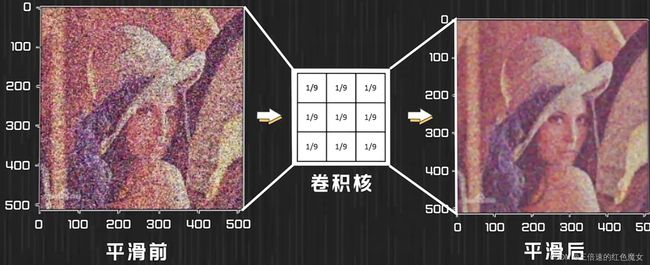
所谓的平滑操作，就是让周围的像素点和自己相差的不要太大。从卷积核的数值1/9看出，它是在求像素点的一个平均值，这个像素点和周围像素点相比，数值是不是太高了？太高了就拉低一点，反之亦然。

这个平滑卷积核实际上规定了 周围像素点如何对当前像素点产生影响
看到这里，是不是感觉很像刚刚的卷积运算可以解决的问题？刚刚我们考虑的是 求t时刻的输出，考虑之前所有的时刻的输入对t时刻产生的影响
现在把它跟数学上的运算对应，如下图：

现在我们想知道最左下角的像素点，对中间的像素点产生了什么影响，之前的卷积运算是把f的函数值跟对应的g函数值相乘，那现在的目标就是去找跟最左下角的f函数对应的g函数

不妨把f(x,y)看成t时刻，把f(x-1,y-1)看成x时刻，
根据卷积公式g(t-x)，可得到g_x = x-(x-1)= 1 g_y = y-(y-1)= 1
则f(x-1,y-1)对应的函数为 g(1,1)
如果把每一个像素点对应的g函数求出来，会发现是这样的对应关系。
看着很难受，把g函数矩阵翻转过来就可以了（懒得画了），这就解释了，图像卷积中的”卷“从何而来。

注意：这里的g函数矩阵不是卷积核，它要180°翻转过来才是卷积核，卷积核是可以直接扣在图像上相乘再相加的，实际操作把旋转省略了，但本质上还是个卷积运算

总结一下，
卷积操作就是 过去对现在是如何影响的，
卷积在图像上平滑操作就是 周围像素点对当前像素点的影响，而平滑卷积核规定了 如何影响

（这里之所以具体到平滑操作，是因为不同的卷积核有不同的功能，不可以都归结为周围像素点对当前像素点是如何影响的这部分单独把平滑卷积核拿来讨论，主要是为了用它说明卷操作下文会详细讲解卷积的另一个作用）

图像卷积的另一个作用-----过滤器

在上文介绍了平滑卷积操作，在卷积神经网络中，并不是所有卷积核都是处理周围像素与当前像素点的关系。

参考 数字识别，通过卷积核处理之后的结果并不是输出跟原图差不多的图片，而是把局部特征提取出来，再将这些特征交给神经网络进行判断。这就不得不提到卷积的另一个作用 ------过滤器

来看下面两个卷积核，第一个卷积核对图像处理之后的结果，得到了垂直方向的边界
第二个卷积核对图像处理之后的结果，得到了左右水平方向的边界

可以发现，这两个卷积核都把图像的某些特征保留下来，把某些特征过滤掉了，比起”周围像素点对当前像素点的影响“，这更像是个主动选择的过程。
这种卷积核就是对特征选择的模板，当你不想考虑这个位置的特征时，就把它设为0

总结一下，目前我了解的卷积核主要有两种功能：
1.平滑卷积核：决定周围像素点对当前像素点的影响
2.过滤器（滤波器）：对像素点的主动选择

解决了上述三个问题，就可以更清楚地知道了卷积操作得到的是什么。因为没涉及到平滑卷积核的操作，下文对问题的解释以滤波器卷积核为主

1.卷积之后会得到什么？

提取了图像特征，找到特定的局部图像特征（如边缘），用在后面的网络中。

2.池化的作用是什么？

减少参数，降低过拟合的风险，加强计算速度
详细解释：图像中的相邻像素倾向于具有相似的值，因此通常卷积层相邻的输出像素也具有相似的值。这意味着，卷积层输出中包含的大部分信息都是冗余的。
如果我们使用边缘检测滤波器并在某个位置找到强边缘，那么我们也可能会在距离这个像素1个偏移的位置找到相对较强的边缘。但是它们都一样是边缘，我们并没有找到任何新东西。
池化层解决了这个问题。这个网络层所做的就是通过减小输入的大小降低输出值的数量。

最大池化：保留最显著的特征

3.池化可以被替代吗？

可以 这个观点出自文献 《Striving for Simplicity: The All Convolutional Net》，作者：Jost Tobias Springenberg , Alexey Dosovitskiy , Thomas Brox, Martin Riedmiller
大概意思就是，用stride=2的conv降采样的卷积神经网络效果与使用pooling降采样的卷积神经网络效果相当；
卷积神经网络小的时候，使用pooling降采样效果可能更好，卷积神经网络大的时候，使用stride=2的conv降采样效果可能更好。
总体来说，pooling提供了一种非线性，这种非线性需要较深的conv叠加才能实现，因此当网络比较浅的时候，pooling有一定优势；但是当网络很深的时候，多层叠加的conv可以学到pooling所能提供的非线性，甚至能根据训练集学到比pooling更好的非线性，因此当网络比较深的时候，不使用pooling没多大关系，甚至更好。

4.池化卷积池化卷积叠加会有什么效果

得到了参数较少，但能保持原始图像信息的特征图

5.flattening宽度多少合适？

不同模型有不同的考虑。
如果全连接层宽度不变，增加长度：
优点：神经元个数增加，模型复杂度提升；全连接层数加深，模型非线性表达能力提高。理论上都可以提高模型的学习能力。
如果全连接层长度不变，增加宽度：
优点：神经元个数增加，模型复杂度提升。理论上可以提高模型的学习能力。
难度长度和宽度都是越多越好？
肯定不是
（1）缺点：学习能力太好容易造成过拟合。
（2）缺点：运算时间增加，效率变低。

文献阅读

《Striving for Simplicity: The All Convolutional Net》，作者：Jost Tobias Springenberg , Alexey Dosovitskiy , Thomas Brox, Martin Riedmiller

ABSTRACT

如今用于目标识别的CNNs大都以相同的原则构建：卷积层与最大池化层交替，接着是少量全连接层。文章重新评估了用CNN从小图像中识别物体的技术水平，产生了对上述结构中不同成分的必要性的质疑。作者发现，在几个基本图像识别数据集上，最大池化层可以简单地被具有更大步长的卷积层代替。根据这种猜想，提出了一种新的架构，其仅由卷积层组成，并且在几个目标识别数据集上(CIFAR-10, CIFAR-100, ImageNet)产生了具有竞争性的或是当前最好的表现。为了分析网络，作者引入了一种新的“反卷积方法”变体，用于可视化CNN学习的特征，它可以应用于更广泛的网络结构。

文章内容

因为对于池化层作用的完整解释很难给出，作者假定池化层通过以上三个方面来对CNN的性能产生帮助：
1.p-norm使CNN的表示更具不变性（invariant）
2.降维使高层能够覆盖输入层的更多部分
3.feature-wise的特性（相对于特征混合的卷积层）更容易优化

在第二点中，作者可以有2中方法得到去除pooling但保留空间降维
1)移除每个池化层，并相应地增加之前的卷积层的步长。
2)用步长大于1的普通卷积替换池层。对于一个k=3,r=2的池化层，可以用一个对应的stride和kernel的卷积层取代，输入个数输出个数一样。）

在第一个方法有一个缺陷
1)显著减少了池化层之前的卷积层的重叠。它相当于一个池操作，其中只考虑左上角的特征响应，可能导致较不准确的识别。
第二个方法则没有这个问题
对于全连接层：
如果最上面卷积层的单元所覆盖的图像区域覆盖了足以识别其内容(即我们要识别的对象)的一部分图像，那么完全连接的层也可以用简单的1×1卷积替换。

前面已经提到了论文网络模型相较于以往CNN的不同之处，在这里进行说明：
1.使用stride大于1的卷积层代替以往CNN中的池化层（下采样层）
2.使用filter大小为1*1的卷积层代替全连接层

文章结论

这篇文章抛弃了以往物体检测CNN网络中的池化层和全连接层，通过实验发现max-pooling层是可以通过 步长>1 的卷积层来实现的，而且不会带来精度的降低，据此提出了全卷积网络。通过使用步长更大的卷积层来代替池化以及使用卷积核为1的卷积层来代替全连接层，在cifar-10和cifar-100上取得了很好的效果，并在imageNet上有很好的竞争力。

可借鉴的思路:

(1)一个只含有Conv层和Subsampling层的网络性能和含有maxpooling层的网络相比，可能差不多甚至更好；
(2)在网络里显式增加（最大）池化层并不总是提升性能，尤其是对于对于其训练的数据集来说，用卷积层就能学到所有的必要的不变量的网络。