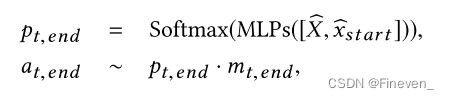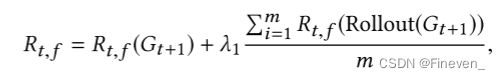论文阅读_XGNN: Towards Model-Level Explanations of Graph Neural Networks
XGNN
abstract
GNN大多时候是一个黑匣子,缺乏人类可理解的解释。如果无法解释GNN模型,在很多场景下是不可应用的。
XGNN在模型级别解释GNN,可以提供高层次和一般性的理解。通过训练图生成器来解释GNN,以使生成的图模型能够最大化明显的某种预测。如果将图生成表示为一个强化学习的任务,对于每个步骤,图生成器都会预测如何将边添加到当前图中。
基于训练后的GNN信息,通过策略梯度训练图生成器。此外,我们还加入了一些图规则,以保证生成的图是有效的。实验结果表明,所生成的图可以为如何改进训练的神经网络提供指导。
Introduction
如果不了解和验证内部工作机制,GNN将无法完全信任,这将阻止其在涉及公平,隐私和安全的关键应用中使用。现有的技术可以分为实例级和模型级两种。
实例级的解释通过确定输入的重要特征或该输入的决策过程来解释对给定输入示例的预测。
模型级别的解释研究哪些输入模式可以导致某种预测来解释模型的一般行为,不考虑任何特定的输入示例,输入优化是最常用的模型级解释方法。两类解释方法从不同的角度解释深层模型。
解释的最终目的是验证和理解模型,我们需要手动检查解释结果,并得出深度模型是否以我们预期的方式工作的结论。对于实例级方法,我们可能需要探究大量示例的解释,然后才能相信模型。然而,这需要时间和专家的广泛努力。对于模型级方法,其解释更加普遍和高级,因此需要较少的人力监督。
与实例级的解释相比,模型级方法的解释不那么精确。总的来说,模型级和实例级方法对于解释和理解深度模型都很重要。
目前还没有关于在模型级别解释GNN的研究,现有研究仅提供了图模型的实例级解释。我们提出了一种称为XGNN的新颖解释技术,用于在模型级别上解释深度图模型。
我们建议研究哪些图模式可以最大化某个预测。具体来说,我们建议训练一个图生成器,以便生成的图模式可用于解释深层图模型。我们将其表述为强化学习问题,在每个步骤中,图生成器都会预测如何向给定的图添加边并形成新图。根据已训练图模型的反馈,使用策略梯度对生成器进行训练。
图生成器只是一个框架,可以根据具体数据集和要解释的GNN推广到任何合适的图生成方法。使用XGNN来解释这些经过训练的模型。实验结果表明,XGNN可以找到所需的图模式并解释这些模型。利用生成图模式,我们可以验证、理解,甚至改进训练过的GNN模型。
Related work
Model-level interpretations
图像数据深度学习模型的流行模型级解释技术,称为输入优化方法,通常会生成优化的输入,该输入可以最大化深度模型的某些行为。他们随机初始化输入,并向目标迭代更新输入。
在这种输入优化技术中,所有网络参数都是固定的,而输入被视为可训练的变量。由于三个限制,它们不能直接应用于解释GNN:
- 图的结构信息由离散邻接矩阵表示,不能通过反向传播直接优化。
- 对于图像,优化的输入是抽象图像,可视化显示了高级模式和含义。就图而言,抽象图没有意义,难以形象化。
- 所获得的图可能对化学或生物规则无效,因为不可微的图规则不能直接合并到优化中。
XGNN:可解释的图神经网络
Model-level GNN Interpretation
直观地说,给定一个经过训练的GNN模型,它的模型级解释应该解释什么图模式或子图模式导致某种预测。
给定一个训练好的GNN,XGNN就要找出子图/图模式。
G*是我们想要找的输入子图,通过图生成来获得的。f(·)是训练好的GNN模型,c是标签。
最大化 G* 被预测为 ci 的概率
Interpretating GNNs via graph generation
对于每个步骤,图生成器基于当前图生成新图。
步骤 t 中将部分生成的图定义为Gt,gθ(·) 是图生成器,Xt 是 Gt 的特征矩阵,At 是 Gt 的邻接矩阵,输出是 Gt+1。
在预先训练的GNN模型指导下训练生成器,公式化为强化学习的问题。
**例子:**假设有 k 种类型的节点,定义一个候选集C={s1,s2,…sk},生成器 g(·) 通过预测向当前图 Gt 添加边来生成 Gt+1。
生成器可以在当前图 Gt 中的两个节点之间添加一条边,或者将候选集 C 中的一个节点添加到当前图 Gt 中,并将其与现有节点连接。
我们将其表述为强化学习问题,由四个要素组成:
状态(state):步骤 t 的强化学习 环境的状态是 部分生成的图 Gt。第一步的初始图可以是来自候选集 C 的随机节点,也可以是基于先验领域知识手动设计的。
行动(action):基于当前图 Gt 生成新的图 Gt+1。action 操作通过确定起始和终止节点向 Gt 添加边,起始节点来自于 Gt,end 结点可以是Gt或候选集C里的,但不能是起始节点。
政策(policy):采用图神经网络作为策略。策略是基于状态可以决定操作,策略可以是图生成器 gθ(·),以Gt和C为输入,输出可能动作的概率。利用reward函数,可以通过策略梯度训练生成器 gθ(·)。
奖励(reward):步骤t的reward可以表示为Rt,用于评估步骤t的动作。reward分为两部分,第一部分在 f(·) 的指导下,鼓励化生成的图最大化 ci 的类分数。第二部分鼓励生成的图在某些图规则方面是有效的。对于每个步骤,我们都包括中间奖励和总体奖励来评估action。
尽管我们将图生成表述为强化学习问题,但 XGNN 是在模型级别解释 GNN 的框架。该框架中的图生成部分可以推广到任何合适的图生成方法,由手头的数据集和要解释的 GNN 确定。
graph generator
对于步骤t,图生成器合并了 Gt 和候选集 C 来预测不同操作的概率,表示为 Pt,start 和 Pt,end。如果 Gt 有 nt 节点,候选集 C 有 k 个节点,那么 P 具有 nt+k 维度。action 从概率中采样,我们从 action 中获得新图 Gt+1。在生成器中,我们首先使用几个图卷积层来聚合邻域信息并学习节点特征。
Xhat 表示学习的节点特征,Gt 和候选集 C 作为 GCN 的输入。我们将C中所有节点合并到 Gt,不添加任何边,可以获得新的特征矩阵和邻接矩阵。使用MLP预测起始节点 Pt,start 的概率,再通过Softmax选择一个概率最大的节点作为初始节点,从概率中采样action。数学上可以表示为
以选定节点为条件,我们使用第二层MLP计算结束节点的概率分布,在结束节点处进行采样。由于起始节点和结束节点不能相同,所以用掩码 mt,end 来屏蔽起始节点。
[·,·]是指广播和串联,at,end 是指除去开始节点,在剩余节点中选择一个节点当结束节点。
Gt有四个节点,候选集C有三个节点,组合在一起形成特征矩阵,再根据Gt形成一个邻接矩阵,一起作为图生成器的输入。使用第一个mlp 获得选择不同节点作为起始节点的概率,并从中采样节点1作为起始节点。然后,根据节点1的特征和所有节点特征,第二个mlp预测结束节点。从概率中进行采样,并选择节点7作为结束节点,它对应于候选集中的红色节点。最后,通过包含一个红色节点并将其与节点1连接来获得新图。
图生成器步骤:
- 合并图 Gt 和候选集 C 的节点,形成特征矩阵。对应的扩展形成相应的邻接矩阵。
- 输入到 GCN 中学习所有节点的特征表示。
- 第一层 MLP 学习预测出起始节点(不能从候选集里选)。
- 第二层 MLP 预测出结束节点(不能与起始节点一致)。
- 将起始节点与结束节点相连接。
Training the graph generator
图生成器经过训练,可以生成特定的图,这些图可以最大化类ci的类分数,并且对图规则有效。步骤t的损失函数:
LCE(·,·) 表示交叉熵损失,Rt 表示reward函数。Rt 表示 at 是否有很大的机会生成具有高ci类分数的图形并且有效。因此,奖励 R t由两部分组成。第一部分 Rt,f 是来自训练模型 f(·) 的反馈,第二部分 Rt,r 是来自图规则。其中 Rt,f 包含对 Gt+1 的中间奖励和最终图形奖励。
其中λ1是超参数,第一项是中间奖励,通过将Gt+1反馈给训练后的GNN f(·) 并且检查 ci 类的预测概率得到。第二项是Gt+1的最终奖励,可以通过在中间图形Gt+1上执行m次获得。每次都是基于Gt+1生成最终图,直到结束。然后使用下式通过 f(·) 进行评估。然后对最终图的评估进行平均,以作为最终图奖励。总体而言,当获得的图倾向于对ci类产生高分时 Rt,f 为正。
l表示f(·) 的可能类的数量。
奖励Rt,r 是从图形规则中获得的,并用于鼓励生成的图形是有效的和人类可理解的。我们采用的第一个规则是,仅允许在任何两个节点之间添加一条边。其次,生成的图不能包含比预定义的最大节点数更多的节点。此外,我们还结合了特定于数据集的规则来指导图的生成。当违反任何这些规则时,将对 Rt,r 申请负奖励。最后,通过结合 Rt,f 和 Rt,r 可以获得步骤t的奖励。
其中 λ1和 λ2是超参数。我们说明了算法1中的训练过程。请注意,当action at 被评估为不能保证 Rt <0时,我们将图Gt+1回滚到 Gt。
算法步骤:
给定一个训练用于图分类的 GNN 模型,表示为 f(·) ,尝试对其进行解释并设置目标类为 ci。令候选集C,生成器 g(·),最大步长为 m,初始图 G1。
- 合并现有图 Gt 和候选集 C。
- 从生成器中获得 action at。
- 根据 at 获得新图 Gt+1.
- 计算 reward 函数 Rt。
- 更新生成器。
如果 Rt < 0,回退 Gt+1 = Gt
experiment
dataset and setup
在合成和现实世界的数据集上评估 XGNN,由于没有现有的工作,所以没有对比的基准线。
**synthetic dataset:**构建了一个合成数据集,称为 is_accyclic,其中提供了基本真相解释。根据图形中是否存在任何循环来标记图形。第一类是指循环图,包括网格状图、循环图、轮图和圆形梯形图。第二类表示非循环图,包含星形图、二叉树图、路径图和全稀有树图。数据集中的所有节点均未标记,我们专注于研究 GNN 捕获图结构的能力。
**real-world dataset:**真实世界数据集 MUTAG 包含表示化合物的图,其中节点表示不同的原子,边缘表示化学键。根据其对细菌的诱变作用,这些图被标记为两个不同的类别。每个节点都根据其原子类型进行标记,并且有七种可能的原子类型: 碳,氮,氧,氟,碘,氯,溴。为简单起见,边缘标签将被忽略。对于此数据集,我们研究了 GNN 捕获图结构和节点标签的能力。
**graph classification models:**我们使用这些数据集训练图分类模型,然后尝试解释这些模型。这些模型共享一个类似的管道,首先使用多层 GCNs 学习节点特征,然后通过平均所有节点特征来获得图级嵌入,最后采用全连接层来执行图分类。我们将 Sigmoid 用作数据集 is_accyclic 的 GCN 中的非线性函数,而将 ReLu 函数用于数据集 MUTAG。
**graph generators:**对于两个数据集,我们的图生成器共享相同的结构。我们的生成器首先采用全连接层将节点特征映射到8维。然后采用三层GCNs,输出尺寸分别等于16、24、32。第一个mlp由隐藏尺寸等于16的两个完全连接的层和一个ReLU6非线性函数组成。第二个mlp还具有两个完全连接的层,隐藏尺寸设置为24并应用ReLU6。
experimental results on synthetic data
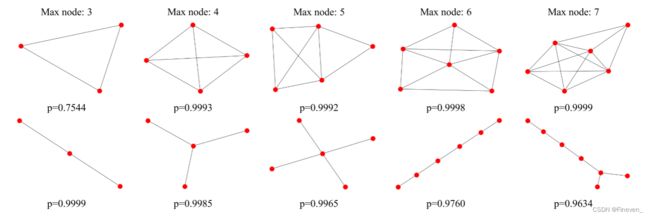
经过训练的GNN分类器可以达到有希望的性能。由于数据集是根据图形是否包含任何圆手动和综合构建的,因此我们可以检查训练后的GNN分类器是否以这种方式进行预测。在第一行显示类 “循环” 的解释,在第二行显示类 “非循环” 的结果。
首先,通过比较为不同类生成的图,我们可以很容易地得出不同的结论,即类 “循环” 的解释总是包含圆,而类 “非循环” 的结果根本没有圆。其次,为了验证我们的解释是否可以最大化某个类的类概率,如等式 (2) 所示,我们将每个生成的图馈送到训练好的GNN分类器,并报告相应类的预测概率。结果表明,我们生成的图模式可以持续产生较高的预测概率。注意,即使对于具有等于3的最大节点数的类 “循环” 获得的图仅导致p = 0.7544,对于具有3个节点的所有可能的图,它仍然是最高概率。最后,根据这些结果,我们可以了解哪些模式可以最大程度地提高不同类别的预测概率。在我们的结果中,我们知道经过训练的gnn分类器很可能通过检测圆形结构来区分不同的类,这与我们的期望一致。因此,这样的解释有助于理解和信任模型,并提高该模型用作圆图检测器的可信度。此外,值得注意的是,与数据集中的图相比,我们生成的图更易于分析。我们生成的图具有明显更少的节点数和更简单的结构,并且产生更高的预测概率,而来自数据集的图具有平均28个节点和30条边,如表1所示。
experimental results on real-world data
由于所有节点都被标记为不同类型的原子,因此我们研究了经过训练的GNN分类器是否可以捕获图结构和节点标签。为简单起见,我们仅包含一个简单的化学规则,即原子的度数不能超过其最大化学化合价。由于节点被标记,我们可以将初始图设置为不同类型的原子。我们首先将初始图设置为单个碳原子,第一行报告 “非诱变” 类的解释,而第二行显示 “诱变” 类的结果。
对于 “诱变” 类,我们可以观察到碳环和NO2是一些常见的模式,这与碳环和NO2化学基团是诱变的化学事实是一致的。
结果表明,经过训练的GNN分类器可能会捕获这些关键图模式以进行预测。此外,对于 “非诱变” 类,我们观察到氯原子广泛存在于生成的图表中,氯、溴和氟的组合总是导致 “非诱变” 预测。通过分析这样的解释,我们可以更好地理解训练好的GNN模型。
将最大节点限制固定为5,并为 “诱变” 类生成解释。首先,无论我们如何设置初始图,我们提出的方法总是可以找到最大化类 “诱变” 预测概率的图模式。对于前5个图,这意味着初始图设置为碳,氮,氧,碘或氟的单个节点,某些生成的图仍然具有常见的模式,例如碳圈和 NO2 化学基团。进一步证实,这些关键模式是由训练有素的 GNN 捕获的。
我们注意到发生器仍然可以产生氯的图,这被预测为 “诱变”,这与我们上面的结论相反。如果所有带有氯的图表都应被确定为 “非诱变性”,这种解释表明了受过训练的 GNN 的局限性。然后,这些生成的解释可以为改进受过训练的 GNN 提供指导,例如,我们在训练 GNN 时可能会更加强调图形氯。生成的解释还可以用于重新训练和改进 GNN 模型,以正确捕获我们所需的模式。
总体而言,实验结果表明,我们提出的解释方法 XGNN 可以帮助验证理解,有助于改进训练后的 GNN 模型。
conclusion
图形模型仍被视为黑匣子,因此不能完全可信。提出了研究图神经网络解释技术的需求。它仍然是一个较少探索的领域,现有方法仅关注图模型的示例级解释。但是,现有的工作都没有研究图模型的模型级解释,该模型更通用,更高级。因此,在这项工作中,我们提出了一种新颖的方法XGNN来解释模型级别的图模型。具体来说,我们建议找到可以通过图生成最大化特定预测的图模式。我们将其表述为强化学习问题,并迭代生成图模式。我们训练一个图生成器,对于每个步骤,它预测如何在当前图中添加一条边。此外,我们还合并了一些图形规则,以鼓励生成的图形有效且易于理解。最后,我们在合成和现实世界的数据集上进行了实验,以证明我们提出的XGNN的有效性。实验结果表明,生成的图有助于发现哪些模式将使训练后的 GNN 的某种预测最大化。生成的解释有助于验证和更好地理解受过训练的 GNN 是否以我们预期的方式做出预测。此外,我们的结果还表明,生成的解释可以帮助改进训练的模型。
note
所提出的XGNN仅证明了其在解释图分类模型方面的有效性,尚不清楚XGNN是否可以应用于节点分类任务,这是未来研究中需要探索的重要方向。