二值化最佳阈值选取方法以及matlab实现
文章目录
- 前言
- 一、真彩色图像转换为灰值图像
-
- 1.转换公式
- 2.转换过程
- 二、最佳阈值选取方法以及matlab实现
-
- 1.迭代法
- 2.双峰法
- 3.最大类间方差法
- 4.最大熵阈值法
前言
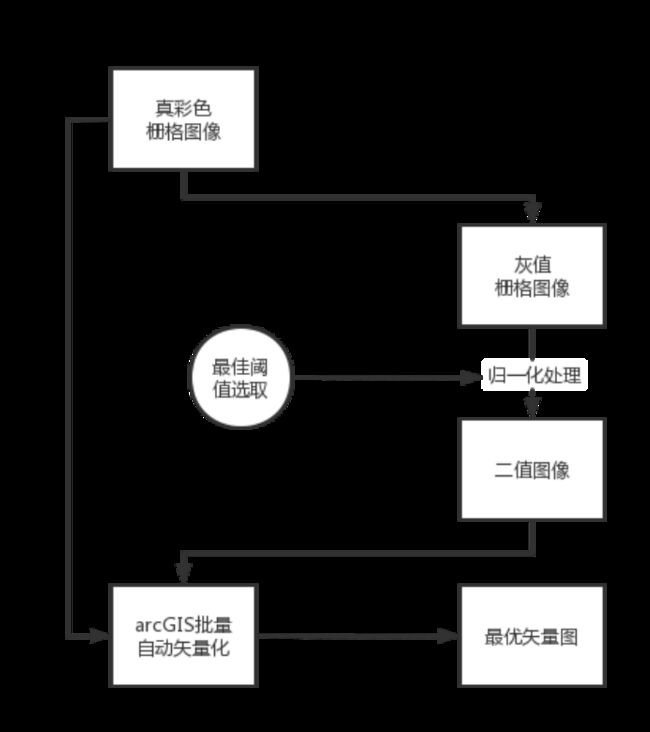
我们利用arcGIS实现对栅格数据的自动批量矢量化时,首先就得需要对栅格图进行二值化处理,即先将真彩色栅格图转化为0~255的灰值图像,然后选取最佳阈值,通过最佳阈值对灰值图像进行归一化处理,最后形成像元值为0和1的二值图像。
那要使自动矢量化的成果能够达到最佳,阈值的选取尤为重要,下面介绍几种常见的阈值选取方法以及matlab代码实现。
一、真彩色图像转换为灰值图像
1.转换公式
![]()
2.转换过程
代码如下(示例):
imshow(imread('影像下载_2208240956.tif'));
title('原始图像');
RGB_image=imread('影像下载_2208240956.tif');
[m,n,l]=size(RGB_image);
pixel=zeros(m,n);
for i=1:m
for j=1:n
pixel(i,j)=0.299*RGB_image(i,j,1)+0.587*RGB_image(i,j,2)+0.114*RGB_image(i,j,3);
end
end
pixel=uint8(pixel);
imshow(pixel);
title('灰白图像');
二、最佳阈值选取方法以及matlab实现
- 迭代法
- 双峰法
- 最大类间差阈值法
- 最大熵阈值法
1.迭代法
基本思路:
迭代法就是利用迭代的方法一次次改变初始阈值,使之与由初始阈值计算的新的阈值之间的差值绝对值达到一个足够小或者某一个定值时,便可以认为此时的新的阈值为最佳阈值。此方法适用于很多的峰值情况的灰值图。
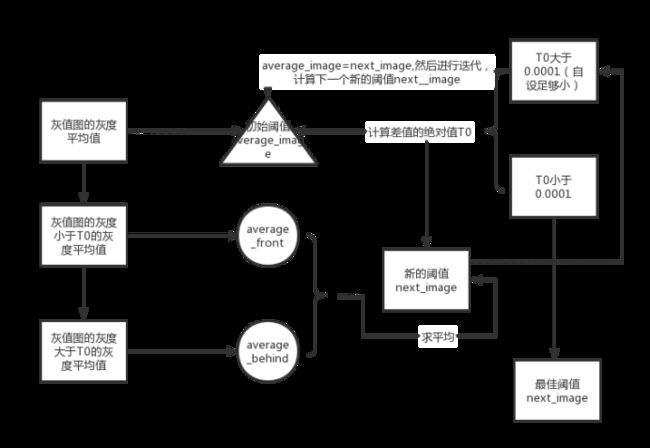
公式:
初始阈值average_image

灰值图的灰度小于初始阈值average_image的平均值

灰值图的灰度大于初始阈值T的平均值

新的阈值:

计算新阈值与初始阈值的差值绝对值
![]()
代码如下(示例):
%迭代平均法
average_image=mean(mean(pixel));%令灰值图像的元素平均值为初始阈值average_image
[rows,cols]=size(pixel);%求解灰值图像的行列元素值
pixel_numbers=rows*cols;%求解灰值图像的元素个数
double_image=double(pixel);%将整型灰值图像转换为浮点类型
%(前景)令灰值图像中大于初始阈值的像元值的总和以及像元个数分别为greater_sum,greater_number
greater_sum=0;%初始化值
greater_number=0;%初始化值
%(后景)令灰值图像中小于初始阈值的像元值的总和以及像元个数分别为less_sum,less_number
less_sum=0;
less_number=0;
%初始化迭代阈值
next_image=0;
%初始化迭代阈值差的绝对值
TO=abs(average_image-next_image);
sigma=0.0001;
number_TO=0;
%开始迭代
while TO>=sigma
%记录迭代次数
number_TO=number_TO+1;
for ii=1:rows
for jj=1:cols
if double_image(ii,jj)>=average_image
greater_sum=greater_sum+double_image(ii,jj);
greater_number=greater_number+1;
end
if double_image(ii,jj)=average_image
double_image(iii,jjj)=0;
else
double_image(iii,jjj)=1;
end
end
end
imshow(double_image);
title('迭代法二值图像','color','r',"FontSize",15)
2.双峰法
基本原理:
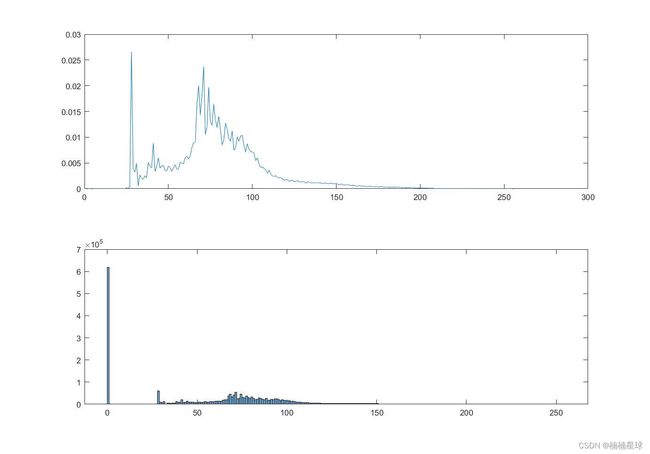
我们知道一般的灰值图的灰度在0~256上都具有一定的规律,首先我们可以先确定其灰度的频率图,然后绘制出便可以发现,如果呈现出两个峰时,我们可以采取两个峰之间的最低值作为最佳阈值。
下面两个图分别是灰值图的灰度频率图和灰度直方图,由于我运算的图像的灰度值大部分都小于1,如果参与阈值的运算,则会导致二值化后的图像丢失大部分信息。因此我剔除了小于1的灰度参与运算,如果换了图像,具体情况视直方图而定。
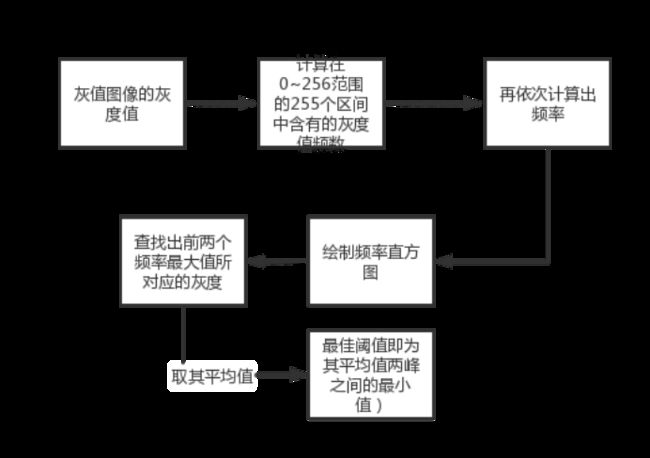
代码如下(示例):
%双峰法,其中pixel为rows*cols灰值图像
m=reshape(pixel,1,pixel_numbers);%pixel_numbers为像元个数,m是对灰值矩阵进行维度转换,便于运算
for op=1:256
%查找出行向量m中各灰度值在1~255的255个区间里的频数
num(op,1)=length(find(m>=op & m=average_image1
double_image1(iii,jjj)=0;
else
double_image1(iii,jjj)=1;
end
end
end
imshow(double_image1);
title('双峰法二值图像','color','r',"FontSize",15)
3.最大类间方差法
最大类间方差法又称为大津法或OSTU算法,是由日本学者大津于1979年提出,是一种自适应的阈值确定方法。根据初始阈值T(取0~256)将灰值图分为G0和G1两个区域,分别计算其类间方差,当方差gt达到最大值时,其对应的即为最佳阈值
灰度值在0~256的255个区间的频率为 num1
公式:
前景G0组的灰度累计占比:

后景G1组的灰度累计占比:

前景G0组的灰度平均值: L=(1~256)

前景G1组的灰度平均值: L=(1~256)

类间方差:
![]()
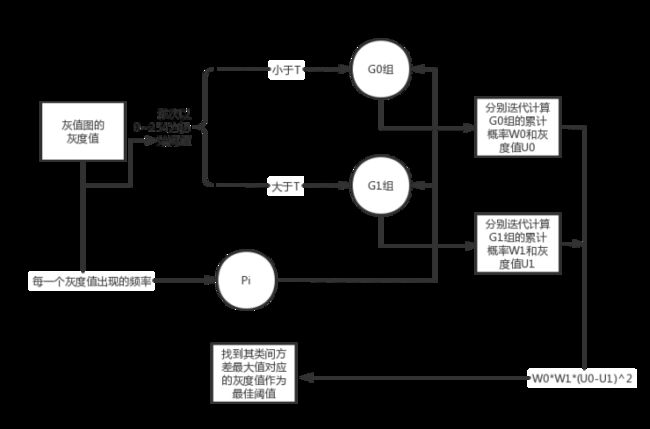
代码如下(示例):
%最大类间方差法
%我们在上一个代码已经算出每一个灰度值出现的概率num1
%G0 包含的像素的灰度值在 0~T,G1 的灰度值在 T+1~L-1
%下面计算当T(阈值)取1~255时第一组W0和第二组W1分别对应的概率和平均灰度值U0和U1
W0=cumsum(num1);
W1=1-W0;
U0=cumsum(X'.*num1);
flip_num1=flip(num1);
U1=flip(cumsum(X'.*flip_num1));
%计算出图像的灰值类间方差以及其gt中最大值对应的灰度值为最佳阈值
gt=W0.*W1.*(U0-U1).^2;
[gt1,average_image2]=max(gt);
double_image2=double(pixel);
for iii=1:rows
for jjj=1:cols
if double_image2(iii,jjj)>=average_image2
double_image2(iii,jjj)=0;
else
double_image2(iii,jjj)=1;
end
end
end
imshow(double_image2);
title('最大类间方差法二值图像','color','r',"FontSize",15)
4.最大熵阈值法
由于能力有限,基本原理大家可以借鉴《图像二值化阈值选取常用方法》
博客网址:http://blog.csdn.net/xgmiao
具体运算公式如下:


代码如下(示例):
%最大熵阈值法
%设阈值 t 将图像划分为目标 O 和背景 B 两类,他们的概率分布分别为
Pt=cumsum(num1);
PO=num1./Pt;
PB=num1./(1-Pt);
%则目标 O 和背景 B 的熵函数分别为
lnPO=log(num1);
for kk=1:256
if lnPO(kk,1)==-Inf
lnPO(kk,1)=1;
end
end
lnPt=log((1-num1));
for kk=1:256
if lnPt(kk,1)==-Inf
lnPt(kk,1)=0;
end
end
%O区域
HO=-cumsum(num1.*lnPO);
HOt=log(Pt)+HO./Pt;
%B区域
HB=-flip(cumsum((1-num1).*lnPt));
HBt=log(flip(cumsum(1-num1)))+HB./(flip(cumsum(1-num1)));
%图像总熵
H=HOt+HBt;
[H1,average_image3]=max(H);
double_image3=double(pixel);
for iii=1:rows
for jjj=1:cols
if double_image3(iii,jjj)>=average_image3
double_image3(iii,jjj)=0;
else
double_image3(iii,jjj)=1;
end
end
end
imshow(double_image3);
title('最大熵法二值图像','color','r',"FontSize",15)