Topic 18. 临床预测模型之缺失值插补方法
桓峰基因公众号推出基于R语言临床预测模型构建方法教程并配有视频在线教程,目前整理出来的教程目录如下:
Topic 1. _临床_标志物生信分析常规思路
Topic 2. 生存分析之 Kaplan-Meier
Topic 3. SCI文章第一张表格–基线表格
Topic 4. _临床_预测模型构建 Logistic 回归
Topic 5. 样本量确定及分割
Topic 6 计数变量泊松回归
Topic 7. _临床_预测模型–Cox回归
Topic 8. _临床_预测模型-Lasso回归
Topic 9. SCI 文章第二张表—单因素回归分析表
Topic 10. 单因素 Logistic 回归分析—单因素分析表格
Topic 11. SCI中多元变量筛选—单/多因素表
Topic 12 _临床_预测模型—列线表 (Nomogram)
Topic 13. _临床_预测模型—一致性指数 (C-index)
Topic 14. _临床_预测模型之校准曲线 (Calibration curve)
Topic 15. _临床_预测模型之决策曲线 (DCA)
Topic 16. _临床_预测模型之接收者操作特征曲线 (ROC)
Topic 17. 临床预测模型之缺失值识别及可视化
Topic 18. 临床预测模型之缺失值插补方法
前言
关于缺失值的处理有很多种方法,既有简单的也有复杂的。我们对常见的几种方法进行简要介绍和评价。
缺失值处理方法
1.直接删除
这种方法简单粗暴,是非专业人士很喜欢用的方式。在缺失数很少的时候,这种方法无可厚非,而且效率很高。如调查了1000人,只有30人缺失,可以考虑删除,通常影响不会太大。但这么理想的情况并不多见,更多的是缺失率较高的情形。有些数据尽管每个变量缺失得都不多,但它们的缺失没有重合,而在分析中,只要有一个变量缺失,就要删除整个观测。因此,如果直接删除,那么需要删除很多个观测,以至于几乎删除了一半。 一般情况下,恰好所有变量都在相同的观测缺失的情况十分罕见,所以,当有缺失数据的变量很多的时候,直接删除会导致样本量大量减少。即使你不在乎分析精度,起码也得考虑一下前期花费的精力吧,相当于你花了100%的精力却只拿到了70%或60%的回报。 所以除非你调查的自变量很少,而且每个自变量缺失得特别少,否则尽量不要采用这种方法。
2.虚拟变量法
虚拟变量法主要用于分类自变量的缺失把缺失值作为一类,这样类别数就多了一类。如性别,本来是男性和女性两类,虚拟变量的话以女性为0、男性为1。如果有缺失,则可以把缺失值赋为2,这样就变成了三类。仍以女性为参照,分别给出男性比女性、缺失比女性的结果,但我们只看男性比女性的结果。 这种方法的好处在于,由于将缺失赋值,统计软件就不会把它当作一个缺失值删除,避兔了由于性别这一变量缺失而导致整个观测被删除的悲剧。 这种方法简单且易于理解,但一般只用于分类自变量,而且对该变量本身而言,样本量仍然变少,储计精度肯定也会变差。另外,对其他变量的估计值有时会有较大影响。所以这也不是一种很好的方法。
3.填补技术——鸟归法
对于缺失值来说,最好的方式当然是把它补上,这就涉及如何填补的问题。填补的方法有很多,简单的如回归填补法,复杂购如多重填补法。回归填补法听起来很简单,也有一定的理论依据,但这种方法有一个问题:容易低估标准误,高估检验统计量。原因很容易理解,在原来的数据中,尽管我们建立了线性方程,但几乎没有恰好位于直线上,总会有一定的偏离,也就是残差。而现在所有的缺失值估计都位于直线上,那就必然导致误差减小,从而使标准误降低。
4.填补技术——期望最大化(Expectation Maximization,EM)算法
EM算法包含两个步骤,即期望步(E-step)和最大化步(M-step)。该算法可能在计算上比较费时,但思路却并不复杂。
5.填补技术——多重填补法(Multiple lmputation,MI)
多重填补是针对单一填补而言的。所谓单一填补,就是对每个缺失值填一个值。这类方法不能反映缺失数据的不确定性,因而容易导致标准误低估,而多重填补是模拟生成一个缺失数据的随机分布,然后从这一分布中随机抽取数据作为缺失值的填补,因而可以反映不确定性。正因为是随机抽取,所以导致多重填补技术存在一个副作用:用该法填补数据会同时产生多组填补值,而且你的填补值跟我的填补值永远都不一样(除非指定同样的种子数)。换句话说,如果你发表一篇填补数据的文章,那么即使我用你的程序重新运行一遍,结果也跟你的不一样(你只能祈祷结果的差别不要太大)。 多重填补技术大概是目前用得最多的一种缺失值填补技术,该法的原理比较复杂,但在软件操作上并不难,所以这里主要介绍一下MI法的思想。
设有缺失值的变量为y,用于预测填补的变量为x(简单起见,设只有一个变量)。利用回归填补法,可以得到 y =a +bx 根据x值可以填补y值。但这样填补后的值,如果再分析y与x的关系,则会使二者的关联人为增大,标准误变低。 为了解决这一问题,很自然的一个想法就是,给y加上一个随机波动项,使y和工之间不是严格的直线关系。即把二者的关系变成 y =a+bx +e 式中,e是一个随机数字(通常可以从残差中随机抽取)。这样一来,y和x之间就不是严格的线性关系,填补的值就不在y = a+bx的直线上了,而是有一定的偏离(偏离大小为e)。通过这种思路,可以使标准误变大一些,更接近实际(EM 算法也用到了这一思想)。 上述方式尽管会使标准误略有增大,但这仍不够,因为它们都是在a+bx的基础上添加一个随机波动的。也就是说,把 a和b这两个系数当作真实参数,而实际上它们只是样本估计值。 我们可以想象一下实际情况:总体的截距和斜率是无法知道的,只能根据当前的一次抽样数据获得样本截距α和斜率b。理论上,如果重复抽样10次,则应该会得到10个a和b,每次计算的α和b肯定会有所不同,它们都只是围绕总体截距和斜率波动的随机值。 因此,为了更加符合实际情况,还需要把α和b也作为随机波动。那怎么把α和b作为随机抽取的值呢?这就需要有一个关于a和b的分布,然后从这个分布中随机抽取a和b。这个分布通常称为贝叶斯后验分布。也就是说,我们要从贝叶斯后验分布中随机抽取α和b,每次抽取的a和b都会有所不同,这样建立的模型也会不同,从而估计的缺失值也是随机的。这相当于用统计的方法来模拟实际,让得到的结果最大可能地接近实际情形。 现在就面临这样的问题:如何产生贝叶斯后验分布并从该分布中随机抽取a和b?目前大多数统计软件采用马尔科夫链蒙特卡罗(Markov chain Monte Carlo,MCMC)模拟的方法。所谓 MCMC,就是两种技术的组合,蒙特卡罗主要是用来模拟抽样,马尔科夫链主要用来产生平稳的分布链。 MCMC的算法极其复杂(幸亏我们有统计软件),但思路还是比较容易理解的,主要步骤如下:
第一步,先利用无缺失的数据作为初始的均数和协方差矩阵(最好使用EM 算法中得到的估计值作为初始值;
第二步,将y中的缺失值利用回归方程填补,并对每一个填补值加上一个从残差中随机抽取的数值;
第三步,利用填补的“完整”数据,计算一个新的均数和协方差矩阵;
第四步,根据第三步中得到的新的均数和协方差矩阵的后验分布,从中随机抽取一个均数和协方差矩阵;
第五步,利用第四步中抽取的均数和协方差矩阵,再回到第一步,把刚才的步骤再执行一遍。
如此多次循环,直到最终的收敛(通常收敛的意思是指,上一次的结果与本次的结果差异非常小甚至无差异)。用最后收敛所得到的填补值作为最终填补值。
缺失数据的单一插补
目前处理缺失数据最常用的方法为完整病例分析(completecase analysis),许多统计软件包中均默认采取此种方法进行模型构建。但研究表明该方法会使结果出现偏差,而且该方法丢弃了许多有用的信息。因此,人们发明了许多插入丢失数据的方法来弥补这些不足。本文主要讨论单一插补。插入平均值、中位数、和众数是最简单的。但这些方法与完整病例分析一样会导致样本平均值和方差的偏倚。此外,这些方法忽略了变量之间的相互依赖关系。回归插入可以保证插入值和其他变量之间的关系。纵向缺失数据的处理还有许多复杂的方法。本文主要讲述如何使用R代码进行单一插补,同时针对我们的读者大多为非统计学专业,文中避免了一些复杂的公式计算和推演。 在大数据临床研究中,数据缺失是普遍存在的。尽管许多原创性研究没有明确地报道他们是如何处理数据缺失的,但在许多统计软件中都有默认处理缺失数据的方法。因此,不同的数据包会有不同的方法处理数据丢失(或者说缺省方法不同),并且用不同的统计软件包处理的结果可能不完全相同。一般情况下这虽然不会导致严重的后果,但是有违科学的公正和严谨。对于这种现象,最好的方法就是在研究方法中明确地阐述如何处理缺失数据。为方便起见,许多研究者将数据不全的病例删除(成行删除),这也是在许多回归分析软件包默认的处理方式]。这种方法仅仅在缺省的数据量不大,或者数据缺失方式为完全随机缺失(missing completely at random,MCAR)和随机缺失(missing at random,MAR)才能获得相对可信的结果。完整病例分析的另一个缺点就是丢弃了一些有用的信息,因为含有缺失数据的观察对象都被删除,而这些信息不全的观察对象含有许多其他有用的信息,这在变量(每一列代表一个变量)数目较多的情况下将会是一个大问题。因为病例删除是基于一个或几个变量缺失,所以可能导致大量的病例被删除。此外,完整病例分析会导致不可预测的偏倚,解决该问题的方法就是数据插入,缺失的数据被插人的数据替代。由于数据插入是当前研究的一个热点,所以有越来越多的数据插人方法被发明。本次旨在介绍一些最基础的缺失数据的插入方法。
1. 数据模拟
为了更好地展示如何进行数据插补,我们首先模拟了150例观察对象。该数据框包含3个变量:性别(sex)、平均动脉压(map)、乳酸(Lac)。为了保证能够得到与本文相同的结果,我们给每一次随机模拟设定了seed值。
set.seed(1234)
sex <- rbinom(150, 1, 0.45)
sex[sex == 1] <- "male"
sex[sex == 0] <- "female"
set.seed(1234)
sex.miss.tag <- rbinom(150, 1, 0.3) #MCAR
sex.miss <- ifelse(sex.miss.tag == 1, NA, sex)
set.seed(1234)
map <- round(abs(rnorm(150, mean = 70, sd = 30)))
map <- ifelse(map <= 40, map + 30, map)
set.seed(1234)
lac <- rnorm(150, mean = 5, sd = 0.7) - map * 0.04
lac <- abs(round(lac, 1))
set.seed(1234)
lac.miss.tag <- rbinom(150, 1, 0.3)
lac.miss <- ifelse(lac.miss.tag == 1, NA, lac)
data <- data.frame(sex.miss, map, lac.miss)
在这些数据中,乳酸被假设为与平均动脉压具有相关性。血乳酸值反应了组织的灌注情况,而后者与平均动脉压有关。我们假定平均动脉压与乳酸的关系为负相关。为了增加随机性,使用rnorm()函数生成截距。假设性别变量的缺失符合MCAR。
sd(lac.miss, na.rm = TRUE)
## [1] 0.407929
summary(lac.miss)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.900 1.700 2.100 2.059 2.400 2.700 38
以上输出结果中我们发现乳酸有47个缺失值,其平均值为2.051,标准差为1.11。
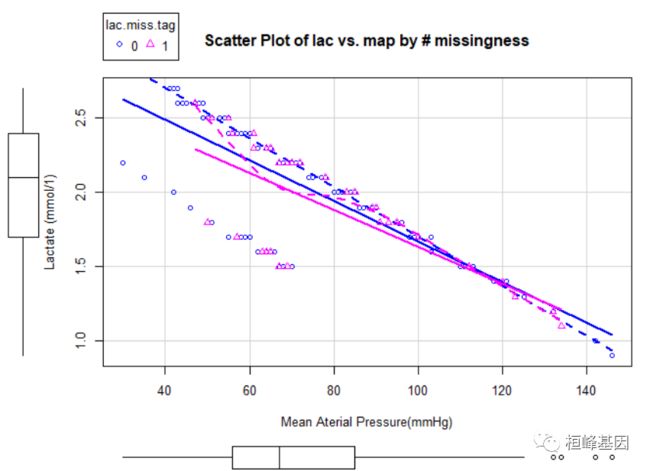
图1是反应乳酸和平均动脉压关系的散点图,乳酸的缺失值以红色三角标注。蓝色和粉色曲线各代表了未缺省和缺省的值的非参数回归拟合。图中显示,缺失的乳酸值均匀地分布在乳酸的取值范围中,并独立于平均动脉压。这符合MCAR的特征。
library(car)
scatterplot(lac ~ map | lac.miss.tag, lwd = 2, main = "Scatter Plot of lac vs. map by # missingness",
xlab = "Mean Aterial Pressure(mmHg)", ylab = "Lactate (mmol/1)", legend = TRUE,
id = list(method = "identify"), boxplots = "xy")
图1散点图反应乳酸和平均动脉压之间的关系,红色三角标注的为乳酸的缺失值
2. 用平均值、众数或中位数估算缺失值
用平均值、中位数或者众数替代缺失值是一种快速简便的方法。R软件中VIM程辑包中的initialise()函数可以完成这项工作。但是,它主要在一些函数的内部使用,而且相对于其他进行单一插入的方法来说并没有什么优势。比如我们希望用平均值给连续变量插入缺失值,以下一段代码返回一个lac.mean变量,该变量包含了完整数据信息,lac.miss中的缺失值用其他值的平均值替代。round()函数用于将结果保留一位小数。
lac.mean <- round(ifelse(is.na(lac.miss), mean(lac.miss, na.rm = TRUE), lac.miss),
1)
lac.mean
## [1] 1.6 2.1 1.6 2.2 2.1 2.0 2.5 2.5 2.5 2.7 2.4 1.5 2.6 2.1 1.7 2.1 2.4 2.6
## [19] 2.6 1.0 2.1 2.5 2.4 2.0 2.6 2.1 1.9 2.1 2.1 2.7 1.7 2.4 2.5 2.4 1.8 2.1
## [37] 2.1 1.7 2.1 2.1 1.5 1.5 2.6 2.3 1.5 2.7 1.5 1.6 2.5 2.1 1.9 2.5 2.1 1.5
## [55] 2.3 1.9 1.4 2.1 1.4 2.1 2.1 0.9 2.2 2.5 2.2 2.1 1.6 1.5 1.5 2.0 2.2 2.1
## [73] 2.4 2.1 1.2 2.3 1.7 2.6 2.1 2.4 2.1 2.3 1.7 2.3 1.8 2.1 1.9 2.4 2.3 2.1
## [91] 2.2 2.1 1.4 1.7 2.5 2.0 1.6 1.8 1.7 2.1 2.0 2.4 2.2 2.4 2.6 2.1 2.7 2.1
## [109] 2.0 2.2 2.1 2.5 2.1 1.8 2.2 2.1 2.1 2.1 1.9 2.1 2.1 2.1 2.1 2.1 1.3 2.2
## [127] 2.5 1.7 2.5 2.1 2.1 2.1 1.6 1.9 2.1 2.4 2.1 2.0 1.7 2.1 2.4 2.1 1.9 2.2
## [145] 2.0 2.0 2.1 2.1 2.1 2.0
接下来,我们用可视化方法检查该缺失值用平均值替代后其分布情况。
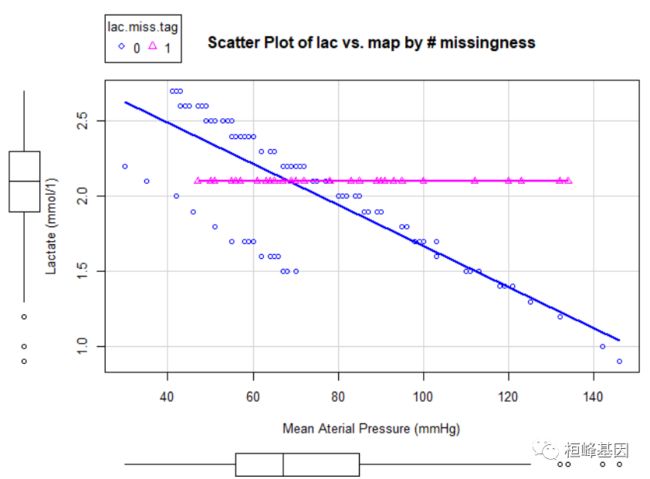
不出所料,所有插入的值都是乳酸的平均值2.1mmol/L(图2),因此该新样本的平均值和标准差与实际样本相比都存在偏倚。众数和中位数的插入也可以用同样的方法插人。虽然这些粗略的方法给缺失值插补提供了方便,但是这种方法低估了方差值(小于实际值),忽略了变量之间的关系,最终使一些统计值(比如均数标准差)产生偏倚。因此,这些粗略估算的方法只能用于处理少量数据缺失,不能被广泛使用。
scatterplot(lac.mean ~ map | lac.miss.tag, lwd = 2, main = "Scatter Plot of lac vs. map by # missingness",
xlab = "Mean Aterial Pressure (mmHg)", ylab = "Lactate (mmol/1)", legend = TRUE,
smooth = FALSE, id = list(method = "identify"), boxplots = "xy")
图2乳酸和平均动脉压关系散点图,缺失值用观察到的乳酸值的平均值来插补
3. 回归插补
依赖于一个或多个变量的回归插补法可能产生更精确的数值。首先,研究者需要为目标变量设定回归方程,含有缺失值的目标变量作为应变量,其他变量作为协变量。利用完整数据进行回归拟合得到回归系数,缺省值就可以根据该拟合的回归模型计算得出。用我们模拟的数据进行举例,乳酸和平均动脉压之间可以建立一个线性回归模型。之后,缺省的乳酸值可根据回归方程得出。
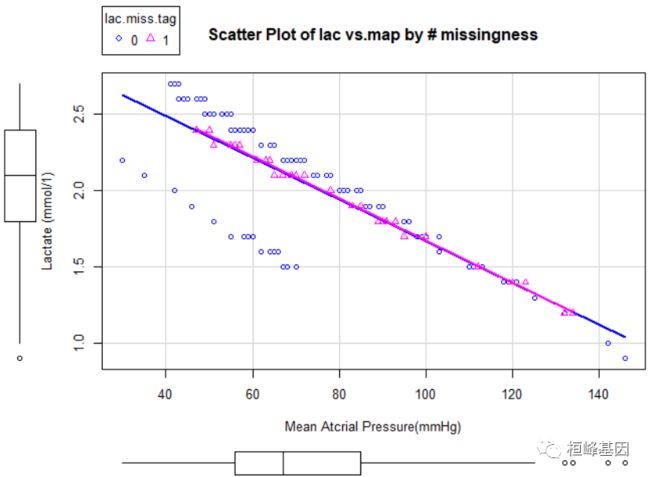
第一行语句拟合了一个线性回归模型。使用了data数据框,该模型存储在fit中。第二句使用predict()函数用回归模型fit去预测乳酸值并存储在矢量lac.pred中。接下来的语句中我们使用了ifelse()函数,使缺失乳酸值用回归模型估算的值替代,而非缺失乳酸值用原先数据替代。接下来的scatterplot()用来绘制图。因为估算值没有设定随机误差,所以都分布在了回归线上(图3)。跟估算平均值相比,这样看起来更具合理性。然而,这种方法增加了乳酸和平均动脉压之间的线性相关性。插补值与随机抽样一样存在随机误差,因此上述方法必定与实际不相符合,因此你也可以使用mice()函数对回归线增加一些随机误差。
fit <- lm(lac.miss ~ map, data = data)
lac.pred <- predict(fit, newdata = data)
lac.regress <- round(ifelse(is.na(lac.miss), lac.pred, lac.miss), 1)
scatterplot(lac.regress ~ map | lac.miss.tag, lwd = 2, main = "Scatter Plot of lac vs.map by # missingness",
xlab = "Mean Atcrial Pressure(mmHg)", ylab = "Lactate (mmol/1)", legend = TRUE,
smooth = FALSE, id = list(method = "identify"), boxplots = "xy")
图3乳酸和平均动脉压关系散点图,缺省值用预先设定好的回归模型预测值插补
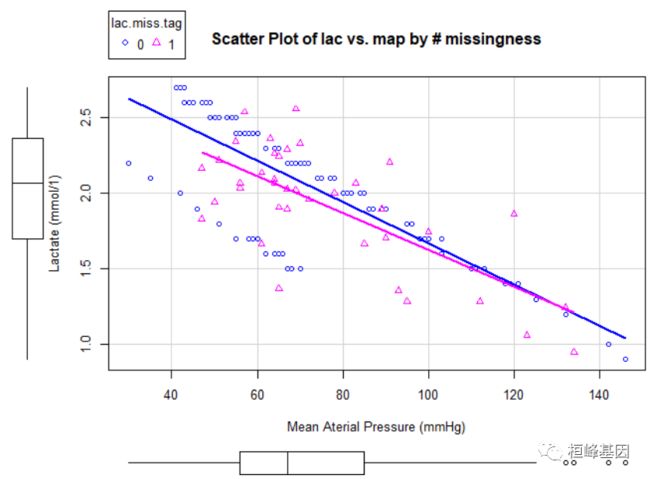
mice()功能的核心是method=“norm.nob”参数,我们设定了“norm.nob”值后,该函数首先估测线性回归的斜率、截距和残差,然后再根据这些拟合系数生成插补值。残差的使用为预测值提供了随机误差,因此从图4我们可以发现这些插补值不再落在一条回归直线上,而是围绕回归线分布。然而,这种方法的一个局限性是可能出现负值,有悖常理。
library(mice)
imp <- mice(data[, 2:3], method = "norm.nob", m = 1, maxit = 1, seed = 123456)
##
## iter imp variable
## 1 1 lac.miss
lac.stoc <- complete(imp, action = 1, include = FALSE)$lac.miss
scatterplot(lac.stoc ~ map | lac.miss.tag, lwd = 2, main = "Scatter Plot of lac vs. map by # missingness",
xlab = "Mean Aterial Pressure (mmHg)", ylab = "Lactate (mmol/1)", legend = TRUE,
smooth = FALSE, id = list(method = "identify"), boxplots = "xy")
图4缺省值用线性回归模型预测,注意,加上了残差来反应预测值的不确定性
4. 指示法(indicator method)
指示法也可以处理缺省值,但这似乎是一种鸡肋的方法,但历史上存在过这种方法,所以此处一并讨论。顾名思义,指示法就是将缺失值进行指示标记,如可以将缺省值设置为0,这样就不再有缺失值,从而保留了每个观察对象里的有用信息。指示法在R语言中能够简单实现。指示法曾风靡一时,因为它简单易行并且能保留全部资料组。另一方面,它允许被观察和缺失数据之间存在系统误差。然而,指示法可能导致回归模型中不可预测的偏差,甚至在只有较少缺失值的情况下,这是其广为诟病的原因。
5. 纵向数据的缺失插补
longitudinalData程辑包中的imputation()函数提供了强大的纵向数据缺失插补计算公式。纵向数据以同一变量重复测量值之间的相关性为特征。因此,与上述提及的方法相比,插补值取决于重复测量的邻近数值而显得更为可靠。比如对于一个给定的患者,其某个时点的乳酸缺失值与临近时间点的乳酸缺失值存在较高的相关性。 假设我们有四名患者,每日测量他们的血乳酸水平。但在数据收集过程中出现了许多缺失值。用R代码生成此数据矩阵的方法如下:
matMissing <- matrix(c(NA, 1.8, NA, 2.3, 2.2, NA, 1.4, NA, NA, 1 - 1, 9.4, 8.4, NA,
9.6, 7.7, NA, 8.1, NA, 7.9, NA, 3.1, NA, 4, 3.3, 3.1, 3.4, 2.4, 3, NA, 2.1, 5.1,
4, 5.6, NA, NA, 4.1, 4.4, NA, NA, 6.2), 4, byrow = TRUE)
matMissing
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,] NA 1.8 NA 2.3 2.2 NA 1.4 NA NA 0.0
## [2,] 9.4 8.4 NA 9.6 7.7 NA 8.1 NA 7.9 NA
## [3,] 3.1 NA 4.0 3.3 3.1 3.4 2.4 3 NA 2.1
## [4,] 5.1 4.0 5.6 NA NA 4.1 4.4 NA NA 6.2
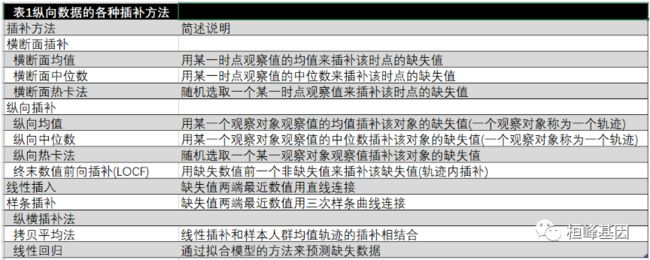
分析这样的资料的第一步就是估算缺失值。由于这些是纵向数据,因此可以认为缺失数据与其前后测量值之间存在相关性。纵向数据插补法采用同一观察对象未缺失数据来估算缺失数据,因此其插补值相对独立于其他观察对象。根据假定该相关性的不同,估算插补值的方法有很多(表1)。本文将阐述几种简单的纵向数据插补方法。读者如果对更复杂的方法感兴趣,可以参考参考文献。
par()函数在设置绘图参数方面有着强大的功能,设置的参数将会应用到随后的绘图过程。mfrow=c(2,2)表示画出的图按照2(行)×2(列)排列。为了形象说明每一种插补方式的特点,使用matplot()函数将实际观察到的和插补的乳酸值标于图上。我们注意到matplot()里面的第一个参数是imputation()函数返回的一个矩阵。Imputation()的第一个参数是一个含有缺失数据的矩阵,每一行代表一条轨迹(trajectory)。第二个参数设定了插补值的具体计算方式,在一系列的例子中笔者依次使用了“crossMean”, “trajMean”,“linearInterpol. locf”和“copyMean.locf”。不同的插补方法会得到不同的插补值(图5)。为了区分观察值和插补值,我们采用matlines()函数用红点和红线标出观察值。
if (!require(longitudinalData)) install.packages("longitudinalData")
library(longitudinalData)
par(mfrow = c(2, 2))
matplot(t(imputation(matMissing, "crossMean")), type = "b", ylim = c(0, 10), lty = 1,
col = 1, main = "crossMean", ylab = "Lactate values(mmol/L)")
matlines(t(matMissing), type = "o", col = 2, lwd = 3, pch = 16, lty = 1)
matplot(t(imputation(matMissing, "trajMean")), type = "b", ylim = c(0, 10), ylab = "",
lty = 1, col = 1, main = "trajMean")
matlines(t(matMissing), type = "o", col = 2, Iwd = 3, pch = 16, lty = 1)
matplot(t(imputation(matMissing, "linearInterpol.locf")), type = "b", ylim = c(0,
10), lty = 1, col = 1, main = "linearInterpollocf", xlab = "Measurement time points",
ylab = "Lactate values (mmol/L)")
matlines(t(matMissing), type = "o", col = 2, lwd = 3, pch = 16, lty = 1)
matplot(t(imputation(matMissing, "copyMean.locf")), type = "b", ylim = c(0, 10),
lty = 1, col = 1, main = "copyMean.locf", xlab = "Measurement time points", ylab = "")
matlines(t(matMissing), type = "o", col = 2, lwd = 3, pch = 16, lty = 1)
图5纵向数据的不同插补方法
MICE程辑包进行多重数据插补
多重插补(multiple imputation,MI)是处理数据缺失较为高级的方法。多重插补优于单一插补,因为和单一插补相比,多重插补考虑到了缺失数据的不确定性。但多重插补在医学文献上未得到广泛应用,因为广大研究人员对该方法仍然不太熟悉,而且在计算上存在一定困难。本文将逐步讲解如何运用R语言的MICE程辑包进行多重插补。多重插补的第一步首先用mice()函数创建m套完整的数据框。接下来在每一套数据框中进行统计描述和统计分析,比如可以利用with()函数进行单变量分析及回归模型的建立。with()函数实质上给数据分析提供了一个环境。最后,用pool函数将从每一套数据框中得到的统计结果整合到一起。 多重插补(MI)是处理数据缺失较为高级的方法。和单一插补相比,多重插补通过缺失数据的插补产生了m个数据框。换句话说,一个原始数据框中的缺失数据,被m个插补值替换产生m套完整的数据框,这样插补产生的不确定 性就被纳入到了分析中。从这m套数据框中估算出来的统计量最后整合成为一个。恰当地运用多重插补可以得到一个和真实总体非常接近的估算值,而单一插补因为偏倚和忽略了估算值的不确定性而饱受争议。然而,多重插补因为未被广泛熟悉以及计算上的难度而未得到广泛应用。为了使临床医生更加熟悉多重插补,旨在介绍如何运用R数据包对缺失数据进行多重插补。首先我们将介绍一下多重插补的基本原理。
1. 多重插补的基本原理
多重插补的过程就是将缺失数据用多个可能的数值替代。与单一插补相比,多重插补的过程更需要考虑估算缺失值引起的不确定性。多重插补会生成多套数据框,再从每个数据框中估算感兴趣的统计量。比如,你对多因素模型中某一协变量的系数感兴趣,那么从m套数据框中就能估算出m个回归系数。最后,再把这些估算的回归系数值整合到一起成为最后的结果,该方法充分考虑到了估算缺失值导致的不确定性。和单一插补相比,这样的插补值和实际值之间的差异会比较小。 多重插补的第一步是为含有缺失值的目标变量建立预测模型,该预测模型利用其他变量作为自变量。而含有缺失值的目标变量即为应变量。在默认情况下,预测平均值配对法(predictive mean matching)用来作连续变量的插补值预测,逻辑回归用来作二分类变量的插补值预测3。
一般来讲纳入预测模型来估计插补值的自变量应该具有以下特征:
1)对缺失有一定的预测作用;
2)与需要进行插补的变量有相关性;
3)本研究中的结局变量。
2. 举例
举个关于乳酸和死亡率之间的关系的研究来作为一个例子说明如何进行多重插补。那个研究的病例数超过3万,采用了MIMIC-II数据库进行研究,而当前这个例子仅有150例类似的患者,假定其中包含了大约30%的乳酸缺失值。下面一段语句生成一个数据框实例,用于展示如何使用R语言进行多重插补。
set.seed(12365)
sex <- rbinom(150, 1, 0.45)
sex[sex == 1] <- "male"
sex[sex == 0] <- "female"
set.seed(123567)
sex.miss.tag <- rbinom(150, 1, 0.3) #MCAR
sex.miss <- ifelse(sex.miss.tag == 1, NA, sex)
set.seed(124564)
map <- round(abs(rnorm(150, mean = 70, sd = 30)))
map <- ifelse(map <= 40, map + 30, map)
set.seed(12456)
lac <- rnorm(150, mean = 5, sd = 0.7) - map * 0.04
lac <- abs(round(lac, 1))
set.seed(134567)
lac.miss.tag <- rbinom(150, 1, 0.3)
lac.miss <- ifelse(lac.miss.tag == 1, NA, lac)
set.seed(111)
mort <- rbinom(150, 1, 0.25)
mort[mort == 1] <- "dead"
mort[mort == 0] <- "alive"
data <- data.frame(sex.miss, map, lac.miss, mort)
3. 利用mice程辑包进行多重插补
R提供了几个较为有用的程辑包进行多重插补。常用的程辑包有amelia,mice和MI。本文主要介绍如何使用mice程辑包对模拟的资料组进行数据插补。首先我们下载和安装该程辑包。
if (!require(mice)) install.packages("mice")
library(mice)
以下语句的最后一行进行了确实数据的多重插补,mice()函数的第一个赋值参数是包含有缺失数据的数据框。第二位置设置了一个seed,以便复制得出结果。由mice()插补得出的结果储存在imp对象中,imp包含了m个包含插补值的完整数据框,以及其他和插补算法有关的信息。接下来我们进一步分析一下imp里面的内容。 由上述的输出可以看出,我们调用了mice()函数,并且该函数生成了5组插补后的完整数据。原始数据框中包含了43个性别缺失值和47个乳酸缺失值。性别变量为而分类变量,因此采用了逻辑回归法进行插补。乳酸为连续变量于是采用了预测均值匹配法。访问序列可以这样定义:
visitSequence = (1:ncol(data))[apply(is.na(data), 2, any)]
visitSequence
## [1] 1 3
该参数决定了变量插补的顺序。在运行示例中,性别缺失值是首先插入的,然后是乳酸缺失值。预测矩阵中包含0和1,用来详细说明哪些变量是用来推断目标变量的。行表示目标变量(将要被插补的变量)。“1”值表示用来预测目标变量的列变量。比如,第一行为sex.miss表示被插补的目标变量是性别,后面跟随的第一个数值为0,因为性别变量不能用于构建模型来预测其本身,后面三个“1”对应的分别为map 、 lac.miss和mort,说明这三个变量都被纳入预测模型用于性别的预测。
predictorMatrix = (1 - diag(1, ncol(data)))
predictorMatrix
## [,1] [,2] [,3] [,4]
## [1,] 0 1 1 1
## [2,] 1 0 1 1
## [3,] 1 1 0 1
## [4,] 1 1 1 0
map和mort行所对应的均为“0”,意味着没有变量是用于预测平均动脉压和死亡率,因为这两者没有缺失值。用户可以随意调整预测矩阵来定义用来预测缺失数据的变量,其表达式可以参考:
library(Rcpp) #Rcpp package is mandatory
library(mice)
imp <- mice(data, seed = 12345)
##
## iter imp variable
## 1 1 lac.miss
## 1 2 lac.miss
## 1 3 lac.miss
## 1 4 lac.miss
## 1 5 lac.miss
## 2 1 lac.miss
## 2 2 lac.miss
## 2 3 lac.miss
## 2 4 lac.miss
## 2 5 lac.miss
## 3 1 lac.miss
## 3 2 lac.miss
## 3 3 lac.miss
## 3 4 lac.miss
## 3 5 lac.miss
## 4 1 lac.miss
## 4 2 lac.miss
## 4 3 lac.miss
## 4 4 lac.miss
## 4 5 lac.miss
## 5 1 lac.miss
## 5 2 lac.miss
## 5 3 lac.miss
## 5 4 lac.miss
## 5 5 lac.miss
imp
## Class: mids
## Number of multiple imputations: 5
## Imputation methods:
## sex.miss map lac.miss mort
## "" "" "pmm" ""
## PredictorMatrix:
## sex.miss map lac.miss mort
## sex.miss 0 0 0 0
## map 0 0 1 0
## lac.miss 0 1 0 0
## mort 0 1 1 0
## Number of logged events: 2
## it im dep meth out
## 1 0 0 constant sex.miss
## 2 0 0 constant mort
假如你不想用死亡率来预测性别,可以用下列方法来更改预测矩阵:
predmatrix <- 1 - diag(1, ncol(data))
predmatrix[c(2, 4), ] <- 0
predmatrix[1, 4] <- 0
predmatrix
## [,1] [,2] [,3] [,4]
## [1,] 0 1 1 0
## [2,] 0 0 0 0
## [3,] 1 1 0 1
## [4,] 0 0 0 0
某一变量的插补值可以通过下述方法来查看。这里使用了head()函数来使查看前6行输出内容,否则输出内容将有47行。
在下面的输出矩阵中我们可以看到mice()函数插补的每一个值。在该例中我们没有明确指出插入值的数量,其默认结果为5个。第一列表示原始资料中含有缺失数据的行数。如果矩阵中包含负值,你则需要检查一下预测插补值的方法是否可靠。通过以下代码,你同样可以查看5个完整资料数据的任何一个。同样使用head()来节省篇幅。用action=4来指定当前查看第4组的插补值。
head(imp$imp$lac.miss)
## 1 2 3 4 5
## 2 3.8 2.3 3.0 2.3 3.7
## 5 4.0 1.7 3.6 0.9 0.4
## 8 2.6 1.4 0.6 0.6 0.6
## 11 2.1 2.1 1.4 0.1 0.6
## 17 2.7 0.9 1.0 2.9 2.5
## 20 2.4 3.8 3.7 2.3 3.7
head(complete(imp, action = 4))
## sex.miss map lac.miss mort
## 1 male 126 0.2 alive
## 2 male 55 2.3 alive
## 3 female 89 0.6 alive
## 4 female 158 0.4 alive
## 5 female 63 0.9 alive
## 6 48 2.5 alive
4. 插入之后的统计分析
现在有5个完整的资料组,传统的统计分析可以进行了。在一般研究中,第一步通常是进行双变量分析,以便找出哪一个变量是和你所感兴趣的预后相关的。下面的例子说明了如何进行t检验以及多变量回归分析。
with()函数的一般形式是with(data, expr),它让R的表达式在一个特定的数据环境中进行,而不是用户工作环境。在我们的例子中,t.test()函数在imp对象包含的5个完整数据组中进行。否则,如果不用with()函数,t.test()将在原始不完整的资料组中进行。以上结果仅仅展示了插补后的第一套完整数据资料,剩下的四套为了节省篇幅而省略了。
接下来,我们看看如何用逻辑回归来找出与死亡率相关的变量。注意在R中逻辑回归用glm()函数来调用。
ttest <- with(imp, t.test(lac.miss ~ mort))
ttest
## call :
## with.mids(data = imp, expr = t.test(lac.miss ~ mort))
##
## call1 :
## mice(data = data, seed = 12345)
##
## nmis :
## sex.miss map lac.miss mort
## 43 0 47 0
##
## analyses :
## [[1]]
##
## Welch Two Sample t-test
##
## data: lac.miss by mort
## t = -0.0014601, df = 60.439, p-value = 0.9988
## alternative hypothesis: true difference in means between group alive and group dead is not equal to 0
## 95 percent confidence interval:
## -0.4008006 0.4002158
## sample estimates:
## mean in group alive mean in group dead
## 2.171930 2.172222
##
##
## [[2]]
##
## Welch Two Sample t-test
##
## data: lac.miss by mort
## t = -0.17322, df = 56.209, p-value = 0.8631
## alternative hypothesis: true difference in means between group alive and group dead is not equal to 0
## 95 percent confidence interval:
## -0.4738909 0.3984523
## sample estimates:
## mean in group alive mean in group dead
## 2.112281 2.150000
##
##
## [[3]]
##
## Welch Two Sample t-test
##
## data: lac.miss by mort
## t = 0.39083, df = 55.349, p-value = 0.6974
## alternative hypothesis: true difference in means between group alive and group dead is not equal to 0
## 95 percent confidence interval:
## -0.3433126 0.5096869
## sample estimates:
## mean in group alive mean in group dead
## 2.069298 1.986111
##
##
## [[4]]
##
## Welch Two Sample t-test
##
## data: lac.miss by mort
## t = -0.5945, df = 56.156, p-value = 0.5546
## alternative hypothesis: true difference in means between group alive and group dead is not equal to 0
## 95 percent confidence interval:
## -0.5698115 0.3089927
## sample estimates:
## mean in group alive mean in group dead
## 2.030702 2.161111
##
##
## [[5]]
##
## Welch Two Sample t-test
##
## data: lac.miss by mort
## t = -0.12363, df = 59.808, p-value = 0.902
## alternative hypothesis: true difference in means between group alive and group dead is not equal to 0
## 95 percent confidence interval:
## -0.4546322 0.4017083
## sample estimates:
## mean in group alive mean in group dead
## 2.092982 2.119444
现在,我们看到罗列出来的对象包括从五个逻辑回归及相关信息得出的结果,其中要注意的是有五套逻辑回归,这里我仅仅展示了第一套插补资料的分析结果。在第一套估算中,lac.miss的回归系数是-0.33。注意sex.miss后面跟着一个“2”,说明水平“1”作为了参考基线,这是R在进行回归分析时处理二分类自变量的一种方法。程序到此并没有结束,我们接下来要将这5套数据得出的统计量进行整合。
mice程辑包中的pool()函数用于将所有估算值结果进行整合,它的赋值可以是一个拟合的模型对象,例如上述语句中我们直接给了fit对象。pool()函数返回一个类似于模型的对象(这里我们可以把它看成是一个模型拟合后返回的对象值),因此可以使用summary()函数来查看整合后的回归系数和相关的统计量。
imp$data$mort = ifelse(imp$data$mort == "alive", 0, 1)
fit <- with(imp, glm(mort ~ sex.miss + map + lac.miss, family = "binomial"))
fit
## call :
## with.mids(data = imp, expr = glm(mort ~ sex.miss + map + lac.miss,
## family = "binomial"))
##
## call1 :
## mice(data = data, seed = 12345)
##
## nmis :
## sex.miss map lac.miss mort
## 43 0 47 0
##
## analyses :
## [[1]]
##
## Call: glm(formula = mort ~ sex.miss + map + lac.miss, family = "binomial")
##
## Coefficients:
## (Intercept) sex.missmale map lac.miss
## -0.378286 0.008136 -0.005199 -0.146408
##
## Degrees of Freedom: 106 Total (i.e. Null); 103 Residual
## (因为不存在,43个观察量被删除了)
## Null Deviance: 120.9
## Residual Deviance: 120.6 AIC: 128.6
##
## [[2]]
##
## Call: glm(formula = mort ~ sex.miss + map + lac.miss, family = "binomial")
##
## Coefficients:
## (Intercept) sex.missmale map lac.miss
## -0.563012 0.035547 -0.004206 -0.107126
##
## Degrees of Freedom: 106 Total (i.e. Null); 103 Residual
## (因为不存在,43个观察量被删除了)
## Null Deviance: 120.9
## Residual Deviance: 120.7 AIC: 128.7
##
## [[3]]
##
## Call: glm(formula = mort ~ sex.miss + map + lac.miss, family = "binomial")
##
## Coefficients:
## (Intercept) sex.missmale map lac.miss
## -0.409619 0.017548 -0.005146 -0.142889
##
## Degrees of Freedom: 106 Total (i.e. Null); 103 Residual
## (因为不存在,43个观察量被删除了)
## Null Deviance: 120.9
## Residual Deviance: 120.6 AIC: 128.6
##
## [[4]]
##
## Call: glm(formula = mort ~ sex.miss + map + lac.miss, family = "binomial")
##
## Coefficients:
## (Intercept) sex.missmale map lac.miss
## -1.483758 0.024071 0.002175 0.106759
##
## Degrees of Freedom: 106 Total (i.e. Null); 103 Residual
## (因为不存在,43个观察量被删除了)
## Null Deviance: 120.9
## Residual Deviance: 120.7 AIC: 128.7
##
## [[5]]
##
## Call: glm(formula = mort ~ sex.miss + map + lac.miss, family = "binomial")
##
## Coefficients:
## (Intercept) sex.missmale map lac.miss
## -0.559824 -0.001561 -0.004196 -0.102210
##
## Degrees of Freedom: 106 Total (i.e. Null); 103 Residual
## (因为不存在,43个观察量被删除了)
## Null Deviance: 120.9
## Residual Deviance: 120.7 AIC: 128.7
pooled <- pool(fit)
pooled
## Class: mipo m = 5
## term m estimate ubar b t dfcom
## 1 (Intercept) 5 -0.678899819 2.0951200250 2.095718e-01 2.3466061566 103
## 2 sex.missmale 5 0.016748184 0.2049824253 2.042590e-04 0.2052275362 103
## 3 map 5 -0.003314242 0.0001488985 9.653017e-06 0.0001604821 103
## 4 lac.miss 5 -0.078374829 0.0810478223 1.111503e-02 0.0943858613 103
## df riv lambda fmi
## 1 71.66097 0.120034236 0.107170149 0.13108706
## 2 100.93228 0.001195765 0.001194337 0.02041465
## 3 83.55784 0.077795421 0.072180137 0.09361828
## 4 60.54608 0.164569987 0.141313951 0.16833957
summary(pooled)
## term estimate std.error statistic df p.value
## 1 (Intercept) -0.678899819 1.53186362 -0.44318555 71.66097 0.6589666
## 2 sex.missmale 0.016748184 0.45302046 0.03697004 100.93228 0.9705819
## 3 map -0.003314242 0.01266815 -0.26161997 83.55784 0.7942583
## 4 lac.miss -0.078374829 0.30722282 -0.25510744 60.54608 0.7995047
总结
数据缺失在临床大数据研究中是普遍存在的。当数据缺失完全随机,且缺失值所占比例不大时,运用完整病例分析法获得可靠的结果。但当变量较多时,完整病例分析法通常会导致数据信息丢失。这时,数据插补法不失为得到更可靠结果的一种选择。本文介绍了几种简单的数据插补法。平均值、中位数和众数插补法虽然比较简单,但它们会使估算样本的统计值出现偏倚,并且这些方法没有考虑到缺失值与其他变量的依赖关系。回归法考虑到了数据之间的依赖关系,但是对缺省值的变异程度估算不准确,变异程度可以通过增加回归模型的随机误差来调整。指示法通过将缺省值设置为0来实现,但这种方法有一定的局限性。纵向数据比较特殊,其缺失值可以通过不同计算方法进行插补。总之,缺失数据的插补是一个热门的研究领域,目前没有哪种方法具有绝对优势,插补方法的选择主要取决于研究者对数据的了解程度。从模拟数据来看,搓贝平均法(copy mean)可能是一个不错的选择。
如何使用mice程辑包进行多重插补,在多重插补生成完整数据资料的时候我们充分考虑到了插补导致的不确定性,这主要体现在插补值是按照一定分布进行抽象的。插入的方法有各种各样,用户可以选择最合适的方法。在大多数研究中,默认设置即可符合要求。with()函数为R表达式运行提供了数据环境,在这里环境的主体就是插补后的完整数据资料。用with()函数我们可以进行t检验等二变量分析,也可以进行多因素回归分析,但任何分析都会得到m份相关的研究者感兴趣的统计量。接着,用pool()函数整合来自每一个完整插补数据框的统计量。从pool()中得到的统计量充分考虑到了插补导致的不确定性。
References:
-
Fox, J. and Weisberg, S. (2019) An R Companion to Applied Regression, Third Edition, Sage.
-
参考《白话统计》
-
参考《聪明统计学》