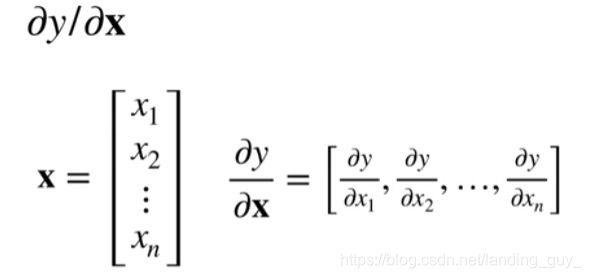对pytorch梯度的理解
文章目录
-
-
-
- 亚导数
- 将导数扩展到向量
- 自动求导的实现
- 梯度清零
- 深度学习中的求导
- 将计算移动到计算图之外
- detach直观理解
- retain_graph=True
-
-
亚导数
- 将导数扩展到不可微的函数
举个例子, 假设是 y = ∣ x ∣ y=|x| y=∣x∣,在 x = 0 x=0 x=0时的导数不存在, 但是我们可以假设其存在, 令其在 − 1 , 1 -1, 1 −1,1之间
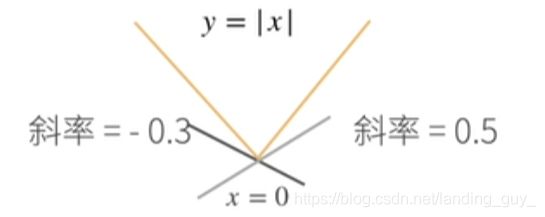

又或者是 y = m a x ( x , 0 ) y=max(x, 0) y=max(x,0) 这个函数, 如下:
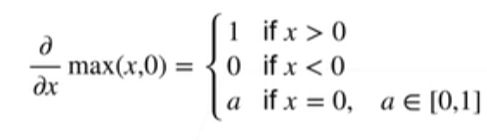
将导数扩展到向量
有这么几种情况
- y是标量,x是向量, 求导是向量
- y是向量, x是标量, 求导是向量
- y是向量, x是向量, 求导是矩阵
- 标量关于列向量的导数是行向量
- y是列向量, x是标量,求导是列向量
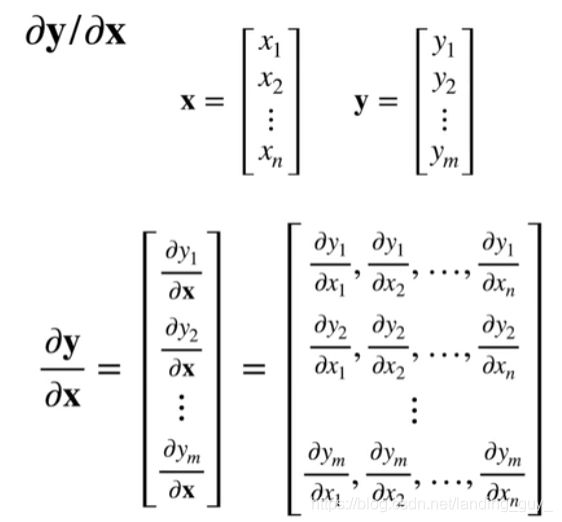
- y是向量, x是向量, 求导是矩阵
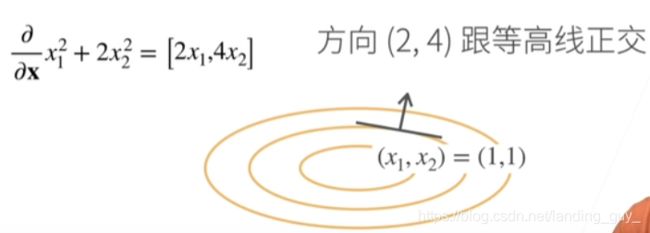
- 怎么理解呢? 可以先从y拆解, 因为y的每个元素是标量对x向量求导得到行向量, 对所有y的元素求导后再排列就是矩阵了
自动求导的实现
假设我们想对函数 y = 2 X T X y=2X^TX y=2XTX 关于列向量X求导
假设X:
import torch
x = torch.arange(4.0)
>> tensor([0., 1., 2., 3.])
在计算y关于X的梯度之前, 我们需要一个地方来存储梯度
x.requires_grad_(True) # 等价于x=torch.arange(4.0, requires_grad=True)
x.grad # 默认是None
y = 2 * torch.dot(x,x)
print(y)
>>
tensor(28., grad_fn=<MulBackward0>)
- 通过调用反向传播自动计算y关于x每个分量的梯度, 因为y是标量
y.backward()
print(x.gard)
>> tensor([ 0., 4., 8., 12.]) # 这和4*x是一致的
梯度清零
在默认情况下, pytorch会累积梯度, 需要清除之前的值
x.grad.zero_()
y = x.sum()
y.backward()
print(x.grad)
>> tensor([1., 1., 1., 1.])
不清零的例子
import torch
x = torch.arange(4.0, requires_grad=True)
y = 2 * torch.dot(x, x)
y.backward()
print(x.grad)
y = x.sum()
y.backward()
print(x.grad)
>> tensor([ 0., 4., 8., 12.])
>> tensor([ 1., 5., 9., 13.])
深度学习中的求导
- 深度学习中, 我们的目的不是计算微分矩阵, 而是计算批量中每个样本单独计算的偏导数之和
x.grad.zero_()
y = x * x
y.sum().backward()
print(x.grad)
- 上面可以看出大部分时间我们是对标量进行求导, 而不是一个向量
将计算移动到计算图之外
x.grad.zero_() # 原来是None的时候会报错, 默认一开始x.grad是None
y = x * x # y是关于x函数
u = y.detach() # 这里相当于把u变为一个单独的常量,导数和x没有关系
# 然后对应u就是一个独立的常量, 值与x有关
z = u * x # 这里对应就是一个常数乘x
z.sum().backward() # 对应的求导就是常数u
x.grad == u
>> tensor([True, True, True, True])
- 加深理解
import torch
x = torch.arange(4.0, requires_grad=True)
print(x)
y = x * x # y是关于x函数
u = y.detach() # 这里相当于把u变为一个单独的常量,导数和x没有关系
y = torch.sum(y) # y是x的平方和
y.backward()
print(x.grad)
x.grad.zero_()
z = u * x # 这里对应就是一个常数乘x
z.sum().backward() # 对应的求导就是常数u, 也就是x的哈达玛积
print(x.grad)
detach直观理解
import torch
x = torch.tensor(2.0, requires_grad=True)
y = torch.tensor(2.0, requires_grad=True)
output1 = x**2
output2 = y**2
output3 = 0.5*output1+0.5*output2.detach()
output4 = 0.5*output1.detach()+0.5*output2
output3.backward()
print(x.grad)
print(y.grad)
output4.backward()
print(x.grad)
print(y.grad)
retain_graph=True
import torch
x = torch.tensor([1., 2.], requires_grad=True)
y = torch.dot(x, x)
y.backward(retain_graph=True)
y.backward()
print(x.grad)