Actionformer: Localizing moments of actions with transformers 论文阅读笔记
论文地址:https://arxiv.org/abs/2202.07925
随着 2020 年 ViT[6] 的出现,基于自注意的 Transformer 模型在图像分类和目标检测方面
取得了瞩目的成果,而近期又在视频理解方面取得了较好的成果。受到 Transformer 的启发,C.Zhang 等人于 2022 年提出了 ActionFormer[35],该模型是第一个 Transformer-based 的 TAL 模型,并且是 anchor-free 的单阶段时序动作定位模型。ActionFormer 结合了多尺度特征表示和局部自我注意,使用一个轻量级解码器对每一时刻进行动作分类并估计对应的动作边界,示例如下图。ActionFormer 在 THUMOS14 上取 t-IoU=0.5 时达到了 65.6% 的 mAP,比之前 state-of-the-art(SOTA) 模型高出了 8.7 个百分点,并首次超过了 60% 的 mAP。
之前的大多数工作基于卷积神经网络来做,且作为two-stage方法需要使用动作提议、生成锚框等;随着性能的稳定增长,提议生成、锚框设计、损失函数、网络架构设计、输出解码过程也越来越复杂。本篇工作意在提出利用Transformer作为基础模块设计一种极简主义的方案,同时要取得足够好的效果。
本文采用的方法是比较简单的,包括用于提取features的backbone,用于投影的浅层卷积网络加堆叠数层Transformer块组成的encoder,和用卷积神经网络实现的decoder。架构如下图所示:

Transformer 最初是为序列数据开发的,它使用自注意力机制来建立长期依赖关系,而
TAL 任务中,视频是未经过剪辑的,且动作持续时间长短不一,因此很适合 TAL 任务。Action Former 集成了局部自注意模型,从输入视频中提取出特征金字塔。输出的金字塔中的每个位置
代表视频中的某一帧,且该位置也是一个候选动作。之后,在特征金字塔上进一步使用一个轻
量级卷积网络作为解码器,将这些候选动作进行分类,并回归出前该动作的开始与结束帧相对
于该动作对应的帧的偏移量。
给定一个输人视频 X X X, 假设 X X X 可以使用一组特征向量 X = { x 1 , x 2 , … , x T } X=\left\{x_{1}, x_{2}, \ldots, x_{T}\right\} X={x1,x2,…,xT} 表示, 这些特征 向量在离散化的时间步长 t = { 1 , 2 , … , T } t=\{1,2, \ldots, T\} t={1,2,…,T} 上取值, 其中 T T T 随视频时长变化而变化, 而 x t x_{t} xt 可以是 从 3D 卷积网络中提取的 t t t 时刻对应片段的特征向量。TAL 的目标是基于输人视频序列 X X X 预测 Y = { y 1 , y 2 , … , y N } Y=\left\{y_{1}, y_{2}, \ldots, y_{N}\right\} Y={y1,y2,…,yN} 。 Y Y Y 由 N N N 个动作类别及其时序边界 y i y_{i} yi 组成, 其中 N N N 也随视频而变化。每个 实例 y i = ( s i , e i , a i ) y_{i}=\left(s_{i}, e_{i}, a_{i}\right) yi=(si,ei,ai) 由动作开始时间 s i s_{i} si (onset), 结束时间 e i e_{i} ei (offset), 和其动作类别 a i a_{i} ai 构成, 其 中 s i ∈ [ 1 , T ] , e i ∈ [ 1 , T ] , a i ∈ { 1 , … , C } s_{i} \in[1, T], e_{i} \in[1, T], a_{i} \in\{1, \ldots, C\} si∈[1,T],ei∈[1,T],ai∈{1,…,C}, 其中 C C C 为提前定义好的类别标签并且 s i < e i s_{i}
模型的输入:视频提取出的特征序列F
输出:序列中的每一个时间点t对应一个三元组 ( p ( a t ) , d t s , d t e ) \left(p\left(a_{t}\right), d_{t}^{s}, d_{t}^{e}\right) (p(at),dts,dte),分别是各个动作类别的置信度,距离动作开始边界的距离,距离动作结束边界的距离。
Encoder
1.将预先提取好的特征送入一个浅层神经网络进行投影,变换到D维的嵌入空间。
2.接着通过L个相同的Transformer块。这里为了减小self-attention固有的高计算复杂度,将自注意改造为局部的,即将注意力限制在一个局部窗口内。在Transformer块之间会穿插降采样层,构成特征金字塔。这里的思想借鉴目标检测中的FPN等特征金字塔网络,不同level的特征的感受野/scale不同,从而能够关注到不同scale的实例,这也适应了动作实例scale差距大且多样的问题。具体来说这个降采样层是由一个带步长的1D深度可分离卷积构成的。这里降采样率设定为2,同时将输出的回归范围也乘以2.
ActionFormer 首先使用编码器 g g g 将输入视频 X = { x 1 , x 2 , … , x T } X=\left\{x_{1}, x_{2}, \ldots, x_{T}\right\} X={x1,x2,…,xT} 编码为多尺度特征表示 Z = { Z 1 , Z 2 , … , Z L } Z=\left\{Z_{1}, Z_{2}, \ldots, Z_{L}\right\} Z={Z1,Z2,…,ZL} 。编码器 g g g 包括:(1) 使用卷积网络将视频编码为特征向量, 每个特征向量 x T x_{T} xT 是 D D D 维的; (2)Transformer 网络将上一步得到的特征进一步编码输出为特征金字塔 Z Z Z 。其中, 卷积神经网络 E E E 以 ReLU \operatorname{ReLU} ReLU 为激活函数, 定义为:
Z 0 = [ E ( x 1 ) , E ( x 2 ) , … , E ( x T ) ] T , Z^{0}=\left[E\left(x_{1}\right), E\left(x_{2}\right), \ldots, E\left(x_{T}\right)\right]^{T}, Z0=[E(x1),E(x2),…,E(xT)]T,
其中 E ( x i ) ∈ R D E\left(x_{i}\right) \in \mathbb{R}^{D} E(xi)∈RD 是 x i x_{i} xi 的特征表示。Transformer 网络进一步将 Z 0 Z_{0} Z0 作为输入, 而 Transformer 的核心是自注意力 (self-attention)。具体来说, 自注意计算输入特征的加权平均值, 其权重与输人特征对之间的相似性得分成比例。例如, 给定 Z 0 ∈ R T × D Z_{0} \in \mathbb{R}^{T \times D} Z0∈RT×D, 其与 W Q ∈ R D × D q , W K ∈ W_{Q} \in \mathbb{R}^{D \times D_{q}}, W_{K} \in WQ∈RD×Dq,WK∈ R D × D k , W V ∈ R D × D v \mathbb{R}^{D \times D_{k}}, W_{V} \in \mathbb{R}^{D \times D_{v}} RD×Dk,WV∈RD×Dv 点乘得到特征表示 Q , K , V Q, K, V Q,K,V, 也即是 query, key, value, 而 D k = D q D_{k}=D_{q} Dk=Dq 。输 出 Q , K , V Q, K, V Q,K,V 的计算公式如下:
Q = Z 0 W Q , K = Z 0 W K , V = Z 0 W V , Q=Z^{0} W_{Q}, \quad K=Z^{0} W_{K}, \quad V=Z^{0} W_{V}, Q=Z0WQ,K=Z0WK,V=Z0WV,
自注意力输出如下:
S = softmax ( Q K T / D q ) V , S=\operatorname{softmax}\left(Q K^{T} / \sqrt{D_{q}}\right) V, S=softmax(QKT/Dq)V,
其中, S ∈ R T × D S \in \mathbb{R}^{T \times D} S∈RT×D, softmax 是按行进行的, 并且多头自注意力 (multiheaded self-attention)(MSA) 进一步并行地增加了几个上述的自注意力操作。MSA 的一个主要优点是能够在整个序列中集成时间上下文信息, 但这种好处是以计算量为代价的。普通 MSA 在内存和时间上的复杂度都是 O ( T 2 ) O\left(T^{2}\right) O(T2) 的, 因此对于长序列来说效率很低, 所以 ActionFormer 通过将注意力限制在局部窗口内。 并且, ActionFormer 使用了 L L L 个 Tansformer 层, 每层由局部多头自注意力模块 (MSA) 和多层感知机 (MLP) 的交替层组成。此外, 在每个 MSA 和 MLP 块之前使用了 LayerNorm(LN), 并在每个块之后都有残差连接, MLP 的激活函数是 GELU。为了捕获不同时间尺度的动作, 可以附带 一个降采样操作 ↓ ( ⋅ ) \downarrow(\cdot) ↓(⋅) 。结构如上图右侧, 公式如下:
Z ‾ ℓ = α ℓ MSA ( LN ( Z ℓ − 1 ) ) + Z ℓ − 1 , ℓ = 1 … L Z ^ ℓ = α ˉ ℓ MLP ( LN ( Z ‾ ℓ ) ) + Z ‾ ℓ , ℓ = 1 … L Z ℓ = ↓ ( Z ^ ℓ ) , ℓ = 1 … L , \begin{gathered} \overline{\mathbf{Z}}^{\ell}=\alpha^{\ell} \operatorname{MSA}\left(\operatorname{LN}\left(\mathbf{Z}^{\ell-1}\right)\right)+\mathbf{Z}^{\ell-1}, \quad \ell=1 \ldots L \\ \hat{\mathbf{Z}}^{\ell}=\bar{\alpha}^{\ell} \operatorname{MLP}\left(\operatorname{LN}\left(\overline{\mathbf{Z}}^{\ell}\right)\right)+\overline{\mathbf{Z}}^{\ell}, \quad \ell=1 \ldots L \\ \mathbf{Z}^{\ell}=\downarrow\left(\hat{\mathbf{Z}}^{\ell}\right), \quad \ell=1 \ldots L, \end{gathered} Zℓ=αℓMSA(LN(Zℓ−1))+Zℓ−1,ℓ=1…LZ^ℓ=αˉℓMLP(LN(Zℓ))+Zℓ,ℓ=1…LZℓ=↓(Z^ℓ),ℓ=1…L,
其中, Z l − 1 , Z ˉ l , Z ^ l ∈ R T l − 1 × D , Z l ∈ R T l × D , T l − 1 / T l Z^{l-1}, \bar{Z}^{l}, \hat{Z}^{l} \in \mathbb{R}^{T^{l-1} \times D}, Z^{l} \in \mathbb{R}^{T^{l} \times D}, T^{l-1} / T^{l} Zl−1,Zˉl,Z^l∈RTl−1×D,Zl∈RTl×D,Tl−1/Tl 是下采样的比例因子, α ℓ , α ˉ ℓ \alpha^{\ell}, \bar{\alpha}^{\ell} αℓ,αˉℓ 是可学 习的每个通道的缩放因子。下采样运算符 ↓ \downarrow ↓ 使用 stride = 1 =1 =1 的 depthwise 1 维卷积实现, 以提升 效率,该模型使用 2 倍下采样。最终结果得到特征金字塔 Z = { Z 1 , Z 2 , … , Z L } Z=\left\{Z_{1}, Z_{2}, \ldots, Z_{L}\right\} Z={Z1,Z2,…,ZL} 。
Decoder
模型的Decoder即简单的分类预测头和回归预测头,只是不同于一般的全连接层实现,而使用一个轻量级的1D卷积网络实现。这个检测头接在特征金字塔各层的特征Z后面,它们共享参数。分类和回归头架构相似,除了分类最后用的Sigmoid激活函数,而回归使用ReLU函数。
Training
损失函数包括分类损失和回归损失,公式如下:
L = ∑ t ( 1 T L c l s + λ reg T + 1 c t L reg ) \mathcal{L}=\sum_{t}\left(\frac{1}{T} \mathcal{L}_{c l s}+\frac{\lambda_{\text {reg }}}{T_{+}} 1_{c_{t}} \mathcal{L}_{\text {reg }}\right) L=t∑(T1Lcls+T+λreg 1ctLreg )
其中T是输入序列长度, 1 c t 1_{c t} 1ct 是指示函数,表示某个时间步 T \mathrm{T} T 是否在动作实例中(正例),若属于背景片段则为 0. T + 0 . T_{+} 0.T+为正例的总数, λ reg \lambda_{\text {reg }} λreg 是用于平衡两种损失的超参数。分类损失使用的是Focal Loss,回归损失使用的是G-loU Loss.损失对特征金字塔各层都做计算.
在训练阶段,还加入了来自目标检测领域的center sampling策略,只有在Ground-Truth动作实 例的中点周围一定区域的时间点才算正例。具体地说,给定动作中点c,范围在
[ c − α T / T l , c + α T / T l ] \left[c-\alpha T / T^{l}, c+\alpha T / T^{l}\right] [c−αT/Tl,c+αT/Tl] 内的时间 t \mathrm{t} t 才算正例。
其中 α \alpha α 是超参数,设定为 1.5. T / T l T / T^{l} T/Tl 为特征金字塔第I层的降采样率。
Inference
利用模型的输出 ( p ( a t ) , d t s , d t e ) \left(p\left(a_{t}\right), d_{t}^{s}, d_{t}^{e}\right) (p(at),dts,dte) ,容易得到动作实例:
a t = arg max p ( a t ) , s t = t − d t s , e t = t + d t e a_{t}=\arg \max p\left(a_{t}\right), \quad s_{t}=t-d_{t}^{s}, \quad e_{t}=t+d_{t}^{e} at=argmaxp(at),st=t−dts,et=t+dte
接着将这些实例进行Soft-NMS减少冗余、重叠部分大的实例,就得到了最终结果。
实验细节
数据预处理。首先使用一个经过 Kinetics[12] 数据集预训练的 I3D[3] 模型来提取视频特征。
具体来说,将 16 个连续的图像帧作为 I3D 的输入,使用一个 stride(步幅) 为 4 的滑动窗口,在I3D 最后一个全连接层之前的层中提取 1024 维的特征。同时,光流帧也按上述操作得到 1024 维的特征。之后再将这两部分的特征进一步 concatenate(连接) 为 2048 维作为模型的输入。
实验参数设置及细节。训练。使用 AdamW[21] 优化器,训练了 30 个 epoch,其中进行了 5 个 epoch 的 linear warm-up(线性热身)。初始 learning rate(学习率) 为 10−3,使用余弦退火进行学习率衰减。batch size(批量大小) 被设置为 2,weight decay(重量衰减) 为 0,momentum(动量) 为 0.9。测试。测试集输入模型的仍然是数据预处理部分提到的 2048 维度的特征,不能达到实时处理的效果,需要先提取视频的特征,这也是该模型的缺点之一。而 soft-NMS 中的 t-IoU 阈值设置为 0.5。
实验结果及分析。作为第一个 TAL 任务下的 transformer 模型的 ActionFormer 在没有任何数据增广的前提下,mAP 高达 66.5%,也使得 TAL 任务的 mAP 首次达到 60% 以上,取得的 state-of-the-art 的 mAP。而 ActionFormer 本身的设计较为简单,仅仅由 Transformer 编码器和轻量级 CNN 解码器组成,就能取得如此好的TAL 任务效果,由此可见,Transformer 是十分强力的一种结构。
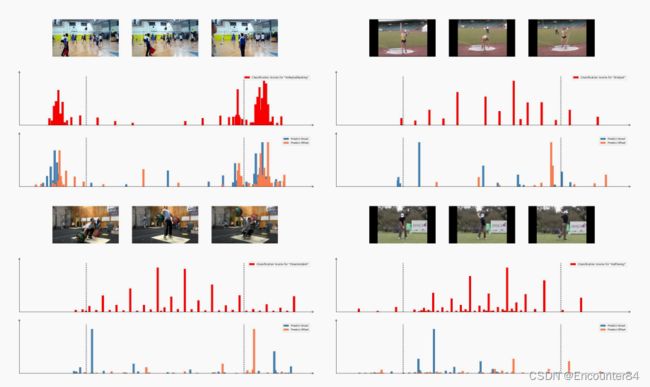
结果可视化分析。如下图,ActionFormer 动作分类得分较高的大多数都处于动作开始和结束时刻中间,也说明了 ActionFormer 作者的先对每一帧进行分类,再回归该动作的边
界的方法的有效性。而对比图 6,可以看到,下方的两幅图,ActionFormer 都能较好地预测动作的起止时刻。而上方的两幅图,结果与 AFSD 类似。