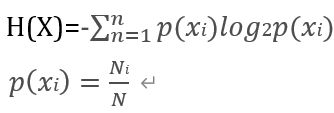决策树分类算法研究及用例

1 题目

• 决策树模型为树状模型，可以实现分类和回归。决策树的训练就是决策树的建树过程。为了实现最优决策树，需要在实际情况中选择不同的算法，在此对决策树的三个算法进行分析比较。

2 理论及算法原理

2.1决策树模型的构成

• 决策树模型由结点和有向边组成，其中结点表示特征空间子集，有向边表示一个划分规则，从根节点到叶子结点的有向边代表了一条决策路径。

2.2决策树的数据结构

• 决策树可以是二叉树，也可以是多叉树。

2.3决策树的功能

• 决策树的实现的分类和预测功能，在分类能力上是十分的强劲，多种算法让机器在分类过程中找到最优的分类的特征进行分类以达到最优决策树。

2.4实现决策树模型的算法

• 比较流行的决策树算法有3种模型：ID3、C4.5、分类回归树(CART)。

2.5决策树生成算法原理

决策树学习的算法通常是一个递归地选择最优特征，并根据该特征对训练数据进行分割，使得各个子数据集有一个最好的分类的过程。这一过程对应着对特征空间的划分，也对应着决策树的构建。

• (1).开始：构建根节点，将所有训练数据都放在根节点，选择一个最优特征，按着这一特征将训练数据集分割成子集，使得各个子集有一个在当前条件下最好的分类。
• (2).如果这些子集已经能够被基本正确分类，那么构建叶节点，并将这些子集分到所对应的叶节点去。
• (3).如果还有子集不能够被正确的分类，那么就对这些子集选择新的最优特征，继续对其进行分割，构建相应的节点，如果递归进行，直至所有训练数据子集被基本正确的分类，或者没有合适的特征为止。
• (4).每个子集都被分到叶节点上，即都有了明确的类，这样就生成了一颗决策树。

3算法对比分析

3.1算法概括

历史上流行的决策树模型有3种：ID3、C4.5、分类回归树(CART)。C4.5是ID3的进阶版，建树过程相似，计算不纯净度的方式不同。可以是二叉树，也可以是多叉树，而CART只能是二叉树，既可以做分类也可以做回归。

3.2算法的基础

• 信息熵：熵表示不确定程度。信息熵越大，信息量越大。
  公式：

  其中N为数据集中的样本数目，Ni为第i个类别数据子集的样本数目。显而易见，p(xi)表示的就是该类别在总样本出现的频率。经过计算得出信息熵，也就是样本类别分布的散布程度。熵越大，表示数据集中的不同类别样本的分布越均衡，数据集越不纯净。

• 经验条件熵：在已有的条件下再次进行，得到的新的熵值，即X后Y的不确定程度
  公式:

经验条件熵表示了各子集中样本的类别分布的平均散布程度，也可视为数据集分为多个子集后的平均不纯净程度。

• 信息增益：信息增益是相对于特征而言的。所以，特征A对训练数据集D的信息增益g(D,A)，定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差。
  公式： g(D,A)=H(D)−H(D∣A)
  信息增益刻画了根据特征A的值，将数据集D分为M个子集后，各子集的平均不确定减少量。

• 信息增益比：特征A在训练集D的信息增益比为g_R (D,A)定义为信息增益g(D,A)关于特征的熵H_A (D)之比
  公式：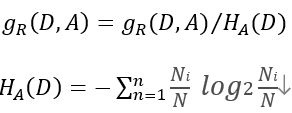

  HA (D)表征了特征A对训练集D的拆分能力。信息增益比本质上是对信息增益乘的一个加权系数，希望增加信息不要以分割太细为代价。当特征A的取值集合较小时，加权系数较大，表示鼓励该特征。

• 基尼指数(Gini Index)：基尼系数最早应用在经济学中，主要用来衡量分配公平度的指标。在决策树CART算法中基尼指数来衡量数据的不纯度或者不确定性。
  公式：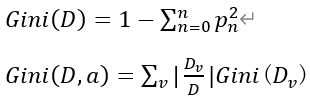

Gini(D,a)表示经过特征a分割后的集合D的不确定性，基尼指数越大，不确定性越大。因此我们需要寻找基尼指数越小的特征作为结点。

• 剪枝：剪枝是指将一颗子树的子节点全部删掉，根节点作为叶子节点。剪枝修剪分裂前后分类误差相差不大的子树，能够降低决策树的复杂度，降低过拟合出现的概率。

3.3算法详情

• ID3算法：ID3算法是决策树的一个经典的构造方法，内部使用信息熵以及信息增益来进行构建；每次迭代选择信息增益最大的特征属性作为分割属性
  优点：决策树构建速度快，实现简单
  缺点：(1).计算依赖特征数目较多的特征，属性最多的特征并不一定最优
  (2).ID3算法不是递增算法，属性不可以重复选择
  (3).ID3算法是单变量决策树，对于特征属性之间的关系不会考虑
  (4).抗噪性差，对缺失值极为敏感
  (5).只适合小规模数据集，需要将数据放入到内存中
  (6).只适用于离散的数据集
  • C4.5算法：在ID3算法的基础上，进行算法优化提出的一种算法；使用信息增益比来取代ID3算法中的信息增益，在树的构造过程中会进行剪枝操作进行优化；能够自动完成对连续属性的离散化处理；C4.5算法在选中分割属性的时候选择信息增益比最大的属性
    优点：(1).产生的规则易于理解
    (2).准确率比较高
    (3).实现简单
    缺点：(1).对数据集需要进行多次顺序扫描和排序，效率较低
    (2).只适合小规模数据集，需要将数据放入内存
• CART算法：使用基尼系数作为数据纯度量化指标来构建的决策树算法就叫做CART（分类回归树）算法。CART算法使用基尼增益作为分隔属性选择的标准，选择基尼增益最小的作为当前数据集的分隔属性；可用于分类和回归两类问题；CART构建的树是二叉树。
  3.4算法对比
  

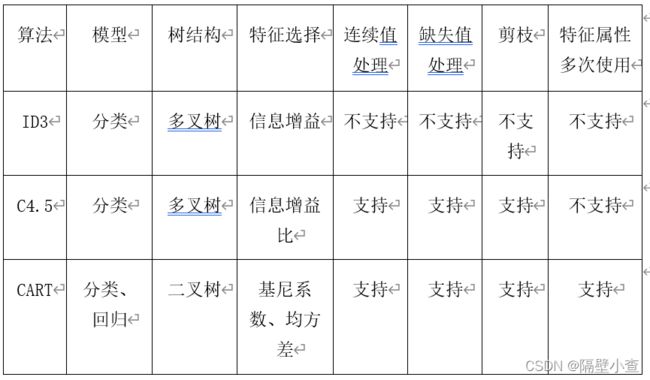
3.5例

已知以社会调查，调查人们对工作好与不好的评判，评判因素主要有工资、压力、平台。工资1为高工资，0为低工资；压力1为压力大，压力0为压力小；平台分别为0、1、2，代表着平台降低。接下来会对此表用三种算法进行决策分类，表如下表所示

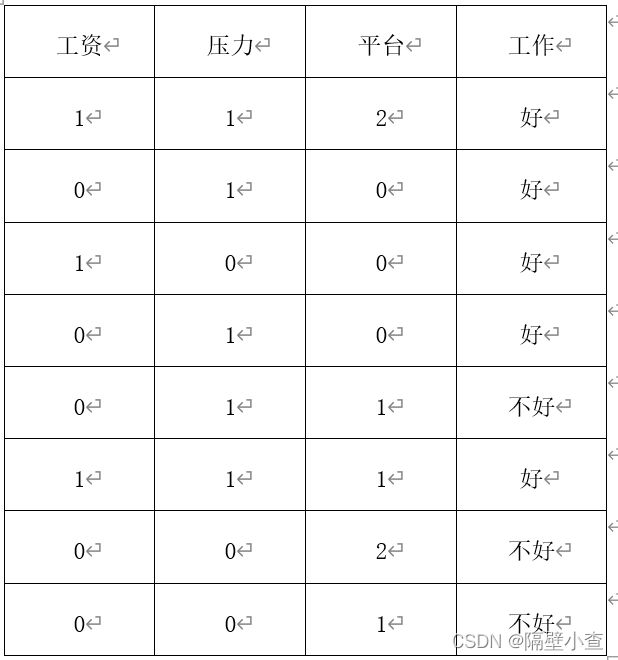
3.5.1 ID3算法

ID3算法选择信息增益最大的特征属性为分割属性
计算整个集合的信息熵：H(D)=-(3/8 log_2⁡〖3/8+5/8 log_2⁡〖5/8〗 〗)=0.95
计算工资的经验条件熵：H(D|工资)= 3/8*(-3/3 log_2⁡〖3/3-0/3 log_2⁡〖0/3〗 〗 )+5/8*(-3/5 log_2⁡〖3/5-2/5 log_2⁡〖2/5〗 〗 )=0.63
得到工资的信息增益为：g(D,工资)=H(D)-H(D|工资)=0.95-1.63=0.34
同理可得：g(D,压力)=H(D)-H(D|压力)=0.16
g(D,平台)=H(D)-H(D|平台)=0.36
因为平台的的信息增益最大，所以选择平台优先选择平台作为特征属性分割。进行迭代该过程，此时数据集被分为三个模块，以三个模块为总数据集进行上述迭代操作，算出其他特征的信息增益，选出信息增益最大的特征作为特征属性再次进行分割。经过计算得出工资的信息增益大于压力的信息增益，所以以工资作为特征属性再次分割，得到多叉树如下图所示

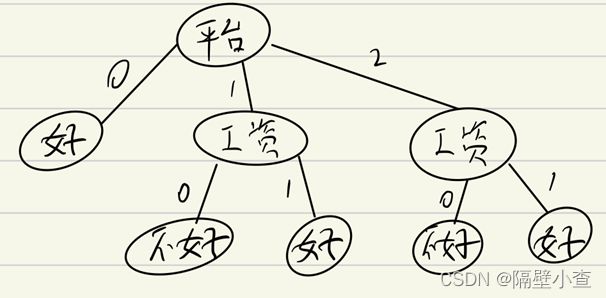
3.5.2 C4.5算法

C4.5算法选择信息增益比最大的特征属性为分割属性
上述内容已算出信息熵与信息增益
计算工资特征的熵：H(工资)=-( 3/8 log_2⁡〖3/8+5/8 log_2⁡〖5/8〗 〗)=0.95
同理计算出：H(压力)=0.95
H(平台)=1.56
计算信息增益比：g_R (D,工资)=(g(D,工资))/(H(工资))=0.34/0.95=0.36
同理计算出：g_R (D,压力)=0.17
g_R (D,压力)=0.23
因为工资的的信息增益比最大，所以选择平台优先选择工资作为特征属性分割。进行迭代该过程，此时数据集被分为两个模块，以两个模块为总数据集进行上述迭代操作，算出其他特征的信息增益比，选出信息增益比最大的特征作为特征属性再次进行分割。经过计算得出平台的信息增益大于压力的信息增益，所以以平台作为特征属性再次分割，得到多叉树如下图所示

3.5.3 CART算法

CART算法选择基尼系数最小的特征属性为分割属性
计算基尼系数并计算出基尼增益：
Gini(D,工资)=3/8*(1-(3/3)^2-(0/3)2 )+5/8*(1-(3/5)^2-(2/5)2 )=0.3
同理可计算出：
Gini(D,平台)=0.37
因为平台有3的属性，CART只能形成二叉树，所以需要对三个条件都进行基尼增益运算：
Gini(D,平台=0)=0.3
Gini(D,平台=1)=0.37
Gini(D,平台=2)=0.46
因为工资和平台=0的的基尼增益最小，所以选择平台优先选择工资或平台=0作为特征属性分割，在此可随意选择，此处选择工资。进行迭代该过程，此时数据集被分为两个模块，以两个模块为总数据集进行上述迭代操作，算出其他特征的基尼增益，选出基尼增益最小的特征作为特征属性再次进行分割。经过计算得出平台=0的信息增益最小，所以以平台=0作为特征属性再次分割，得到多叉树如下图所示

3.5.4 例题显示的各算法的区别

• ID3算法计算依赖特征数目较多的特征
• 三种算法都可适用于离散型数据集
• CRAT只能形成二叉树等

4总结

学习机器学习，了解人工智能，让我们了解到了计算机科研的前瞻。决策树是机器学习的一小部分较为简单的模块，学习该模块让我也回顾了不少的数学理论知识，也学习了算法的精妙。很佩服发明该算法的人，很感叹知识的奇妙，感叹到自己所掌握知识的贫乏。在之后应加强学习，好了解很多知识才能突破自己，升华人生。

5参考文献

[1]卿来云, 黄庆明. 机器学习从原理到应用[M]. 第1版. 北京:人民邮电出版社, 2020年10月 :105-118.
[2]Jonny的ICU. 决策树的剪枝操作[EB/OL]. 2017年7月[2021年12月1日]. https://blog.csdn.net/m0_37338590/article/details/75266989.
[3]呆呆的猫. 机器学习实战（三）——决策树[EB/OL]. 2018年3月[2021年12月1日]. https://blog.csdn.net/jiaoyangwm/article/details/79525237?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522163871318916780255211529%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=163871318916780255211529&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_alltop_positive~default-1-79525237.pc_search_es_clickV2&utm_term=%E5%86%B3%E7%AD%96%E6%A0%91&spm=1018.2226.3001.4187.