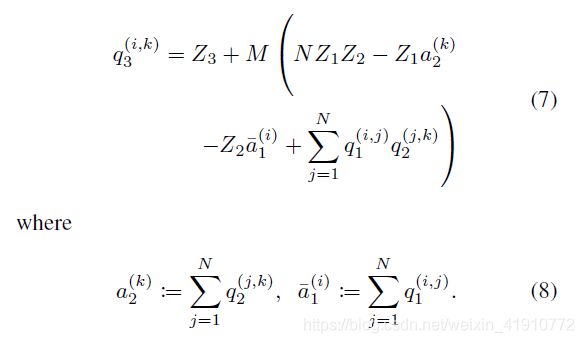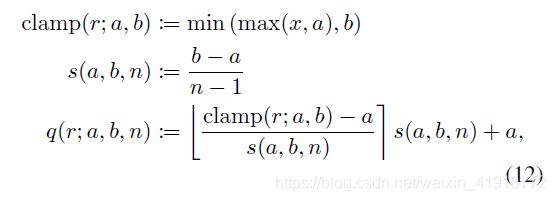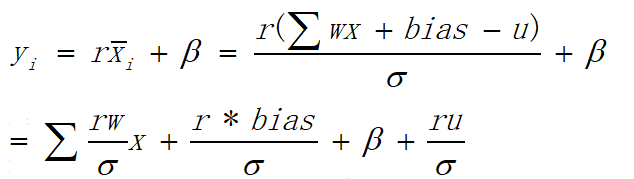神经网络量化----吐血总结

 神经网络量化----吐血总结

---

目录

 神经网络量化----吐血总结

1. 前言

1.1 量化是什么？

1.2 量化会带来什么？

2. 量化具体介绍

2.1 非对称量化

2.2 对称量化

2.3 随机量化

2.4 量化感知训练

3. 经典量化论文解读

3.1 Google 8-bit Integer-Arithmetric-Only Inference

---

---

1. 前言

本文主要借鉴于Google关于量化的白皮书，Quantizing deep convolutional networks for efficient inference: A whitepaper
并感谢666DZY666大佬的开源项目：https://github.com/666DZY666/model-compression 
能力有限，若有描述不当的地方，请大佬勿喷，仅为学习使用，若侵权，请告知，立删。

1.1 量化是什么？

量化是模型压缩的一种方式。量化就是把高位宽（例如32float）表示的权值或者激活值用较低位宽来近似表示（int8），在数值上的体现就是将连续的值离散化。

1.2 量化会带来什么？

量化主要用在边缘计算等硬件限制较大的场景下，即工业应用上（总不能在边缘上都带着GPU吧）。现有很多先进的神经网络（例如resnet，densenet）在分类、识别上都取得了较好的效果，但其普及程度远不及效果稍差但模型小、运算快的mobilenet，而mobilenet就是在权衡速度、识别率下产物。当然了，mobilenet不是量化模型，只是用来举个例子，用于说明量化的潜力。

以下为量化所带来的一些影响：

• 优点1：加快运算速度。当把32float转变为int8表示时，在不考虑系统有浮点加速模块时，定点运算要比浮点运算快，感兴趣的可查阅定点数和浮点数运算的区别
• 优点2：减少存储空间。若将32浮点数转变为8位表示时，存储空间减小到了1/4大小。
• 缺点1：在用低带宽数值近似表示时，会造成一些精度损失。值得高兴的是，神经网络的参数大多是冗余的（或者说是对噪声的容忍度），所以当在近似变换时对精度的影响不是特别大。

下面用图来说明量化是怎么带来损失的，A为实际的浮点值，量化后近似为B，但其表示的值为C点，缩放因子越大，A和C的距离就越远，误差就越大，所以在量化时引入的近似会带来一些精度上的损失。（后面会具体讲解如何设置最值，来找到合适的缩放因子）
 

---

2. 量化具体介绍

2.1 非对称量化

本文都以量化到8-bit为例
1）首先，设置浮点数的最大值x_max,最小值x_min：

• 对于权重：权重在训练后大小都是固定的，一般直接求出权重的最大值和最小值。
• 对于激活值：会随着输入值的改变而改变，所以不能直接求其最值，google使用了滑动均值平均的方法，TensorRT使用KL散度，Easyquant使用cos相似度，后面会具体介绍。

2）其次，设置要量化的范围x_q_max,x_q_min，在非对称量化下为[0,255]。
3）之后，计算缩放因子Scale(float32)和平移因子Zero_point(int8):      
                                                           ,  
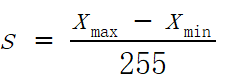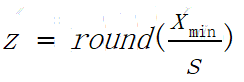
4）最后进行量化和解量化：图中的N_levels-1为255，round为四舍五入
         
然而为什么是在量化时使用先放缩再移位，解量化时先移位再放缩呢？可不可以反过来呢？答案是否定的，主要从效果和运算两个方面考虑：

       在运算上，主要考虑如何使用整形运算代替浮点运算，可以参考google论文（后面会有详细介绍）
      在效果上，主要考虑关键数0，浮点中的0的关键用法主要在于补零padding和激活Relu上，所以为了保证量化效果，需要将浮点0无偏差的使用整形来代替。可以参考这里，详细解释如下：
两种解量化方法如下：
    （讨论的解量化）
  （本文中的解量化，先移位再放缩，上下文移位的正负号一致性请忽略）
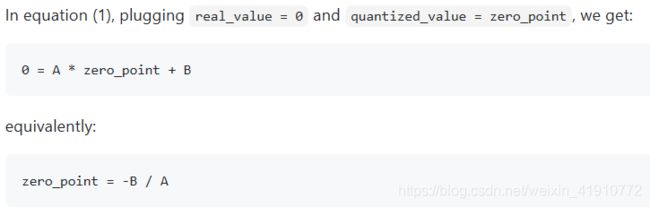
对于第一种，让real_value为0，得到的zero_point如下，很难保证zero_padding为整形，因为缩放因子为浮点数。
 
而对于第二种，是不是就很完美了，zero_point很自然的就是整形了。
  

 

2.2 对称量化

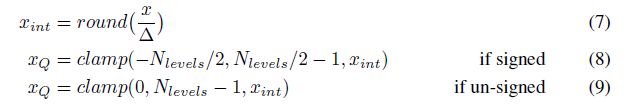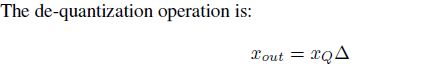对称量化可以看作非对称量化的一种特殊形式，怎么特殊呢？无非就是将zero_point设置为了0，在量化时不考虑移位的概念，那么量化的坐标轴就是对齐的了。具体如下：  （量化）
                             （解量化）
因此，计算缩放因子时就没有了最小值的概念，全部使用绝对值的最大值。如下：
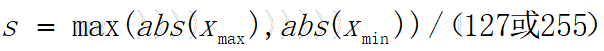 （除以127为有符号数，除以255为无符号数）
对称量化相当于简化了网络部署的运算，那么精度必然要稍微降低一点点。但是既然敢这样简化，必然有相对应的策略的，有兴趣的可以研究8-bit inference with TensorRT的做法，论文点这里，视频点这里，比较好的博客点这里。
具体如下：
1）TensorRT认为对于权重没有提升的空间，因此，在对权重量化时，采用了和Google一样的形式，直接求最值。
2）而对于激活值，相当于做了两遍inference，第一遍，测出激活值的最值，然后根据最值划分直方图。第二次设置阈值量化，然后根据两次的KL散度来找出最佳的阈值。

2.3 随机量化

即在量化时加入噪声，可能在量化感知训练时比较有效，以后再研究post-train量化。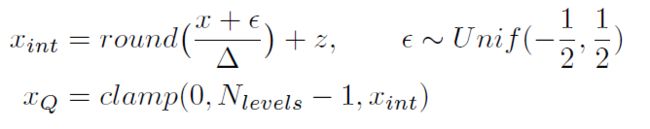

2.4 量化感知训练

在讲量化感知训练之前，首先说一下训练后量化（post-train quantization），直接拿在浮点域下训练好的神经网络模型进行量化可以不可以呢？当然可以，尤其在大网络下，参数的冗余程度较大，量化的效果还是挺可观的，例如：Easyquant直逼32float全精度的准确率。但是在小网络下，效果并不好，有的很差，例如Google的训练后量化在Mobilenet下识别几乎为随机事件。什么原因呢？主要有两种：
1）不同channel下的激活值的分布差异较大，导致1.2中我们所讲的带来较大损失。使用channel这个level下的量化会解决这个问题。
2）异常权重的出现会导致权重的量化出现较大损失，那么为什么不在量化权重的时候加上阈值或者使用KL散度呀，是有的，不知道是不是Easyquant，后续会补充。

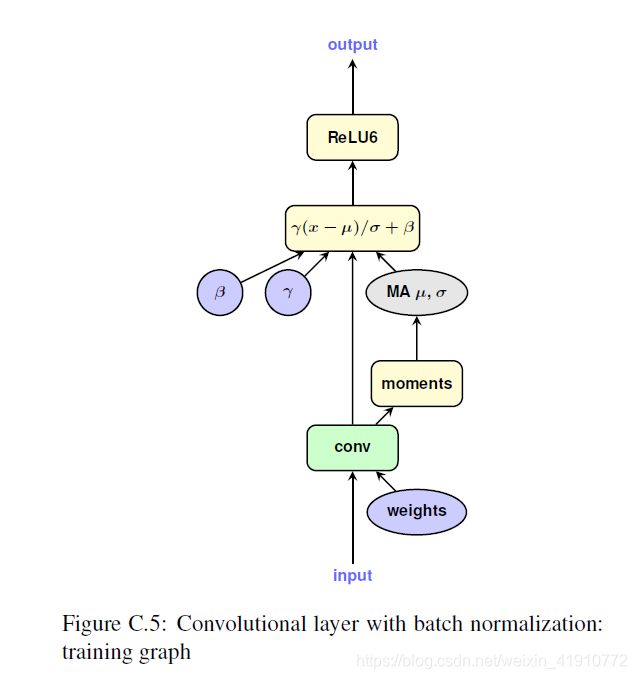
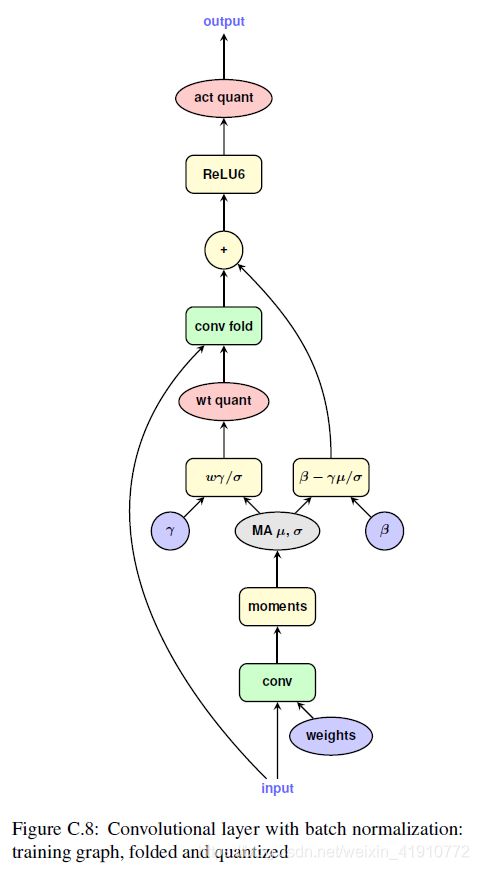
OK！那么有没有一步到位的方法呢，现在引出量化感知训练，如下图，用前向传递来模拟量化所带来的误差，神经网络可以被训练到量化误差较小的位置。
                                   
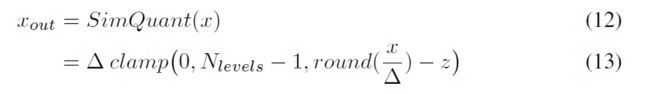
计算误差时使用量化后的输出计算，在后向传播时则不考虑量化的部分，听起来有些抽象，下面来看一段代码（pytorch），本人就因为需要研究量化理论才从keras跳到pytorch的，友情建议一下，如果有修改网络的需求的话，尽量不要使用keras了，keras高度API好用些，但不容易对内部进行改写（尝试过把源代码抽出来进行改写，不是很方便）。

class Round(Function):

    @staticmethod
    def forward(self, input):
        output = torch.round(input)
        return output

    @staticmethod
    def backward(self, grad_output):
        grad_input = grad_output.clone()
        return grad_input
class Quantizer(nn.Module):
    def __init__(self, bits, range_tracker):
        super().__init__()
        self.bits = bits
        self.range_tracker = range_tracker
        self.register_buffer('scale', None)      # 量化比例因子
        self.register_buffer('zero_point', None) # 量化零点

    def update_params(self):
        raise NotImplementedError

    # 量化
    def quantize(self, input):
        output = input * self.scale - self.zero_point
        return output

    def round(self, input):
        output = Round.apply(input)
        return output

    # 截断
    def clamp(self, input):
        output = torch.clamp(input, self.min_val, self.max_val)
        return output

    # 反量化
    def dequantize(self, input):
        output = (input + self.zero_point) / self.scale
        return output

    def forward(self, input):
        if self.bits == 32:
            output = input
        elif self.bits == 1:
            print('！Binary quantization is not supported ！')
            assert self.bits != 1
        else:
            self.range_tracker(input)
            self.update_params()
            output = self.quantize(input)   # 量化
            output = self.round(output)
            output = self.clamp(output)     # 截断
            output = self.dequantize(output)# 反量化
        return output

以下有点需要对代码进行说明：

1）继承nn.module的类中一般需要定义前向传播函数即forward（），其他的quantize(), dequantize(), round(), clamp()等都是为forward服务的。
2）Tensor的自动求导机制，是根据内部的节点计算而来的，而clamp(), abs(), 2*out等等都是不会影响梯度的，pytorch的register_buffer就类似常量的概念，不会对其进行求导。
3）对round函数的改写，定义了前向和后向传播函数。虽然在2中讲到这些特殊的运算不会影响梯度大小，但会阻止损失的后向传播，因此需要对round()重新定义。
4）怎么使用这个函数，定义一个conv2d的类，在forword()中加上conv2d函数，并在之前加上相关的量化函数即可。
5）需要对代码修改的部分：在forword中需要定义training时更新参数，不然每推断时都会对参数进行更新；在定义module时需要将在forword中return output，不然summary时会报错。
6）对截断操作的理解：有些人可能会疑惑，为什么截断操作可以让神经网络往量化误差小的方向训练呢，从求导的方式我也很难讲清楚，所以可以试试从概念上理解一下，那就是截断操作可以消除异常值对误差的影响，也就是说网络会弱化生成异常值的网络节点，从而异常值的截断操作没那么重要了。

关于梯度的测试代码如下：

import torch
import torch.nn as nn

inp = torch.ones(1, 1, 4, 4)
conv = nn.Conv2d(1, 1, 3)

out = torch.abs(conv(inp))  #在前向传播中使用abs函数
loss = torch.mean(out)
loss.backward()  #反向传播求导
print(out.data)
print(conv.weight.grad.data)  #梯度被正常计算出来了

# out = torch.clamp((conv(inp)), -0.1, 0.1)  #在前向传播中使用clamp函数
out = torch.round(conv(inp))  

# out = out *2
# print(out.data)
loss = torch.mean(out)
loss.backward()  #再一次反向传播求导
print(conv.weight.grad.data)  #梯度还是被正常计算出来了

---

3 经典论文解读之 Google 8-bit Integer-Arithmetric-Only Inference

谷歌的这篇论文不是量化的开山之作，但为什么讲它的？真的是有新奇之处的，比如量化部署的计算，BN的处理方式，量化感知训练等，，，

论文链接：Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference

3.1 量化方案

采用非对称的量化方案，文章中有示例卷积是怎么通过8bit进行运算的，如下：

也就是说只要知道输入的8-bit weight和8-bit activation，那么就能得到输出的8-bit activation，整个计算中，除了M为浮点值外，其他的运算都是整数。而在量化网络下是最好不要涉及到浮点运算的，而文章也有提出他们的想法：

 

个人的一些想法：

• 文中所说的M0在[0.5,1）的范围，是经过实验得到的，然后使用32位定点数来表示这个小数，之后通过和定点数相乘再移位的方式来达到浮点计算的效果。
• 在实际计算时，可以简要这一步骤，不管M是什么，那么既然是浮点数，就可以近似表示为整数加移位的组合，而和浮点数相乘那就是可以先和整数部分相乘，再进行移位。

经过简化，可得以下公式：

分析简化前和简化后的复杂度，上述的两个N*N的矩阵相乘，可得N*N个值，为方便叙述，在这里称之为N*N个单位。简化前，每个单位有（2N个减法+1N个乘法），共（2N^3个减法，N^3个乘法）；简化后，总共需要求出N次a1的行均值、a2的列均值，因此只需要2N^2次加法，简化了很多吧！简化的优点：减小了复杂度，将乘法运算控制在16-bit以内。要不说google牛逼呢。

若存在偏置的话，该怎么处理呢？不慌，因为以上的乘加运算在32-bit中进行，故也将偏置映射到32-bit中，设置为s1*s2，zero_point为零。得到以下公式：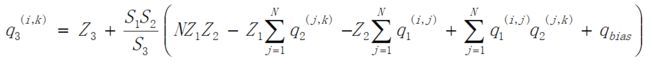

3.2 量化感知训练

关于训练后量化，这里不做过多阐述，有兴趣的可去阅读原论文。

1）conv

    Google在网络将要做运算之前，插入伪量化节点，对参数和激活值做离散化处理，如下图：

    量化操作如下：

• 先截断，将其限制在设定最大值最小值之间，这里可能会有人疑问，其值肯定在最大值和最小值的范围内呀，为什么要限制呢？这里埋藏个问题，后面讲到最大值和最小值的设定你就懂了。
• 再量化
• round一下
• 再反量化    注（公式中的量化和反量化貌似和我第二章讲的相反了，并且Google的量化感知训练和训练后量化也相反了，这里就不清楚为什么了，并没有文档对其解释，我的理解是当使用了量化感知训练时两者的差别不大，又或者说是部署框架的需求。）

2）BN和conv的融合

    首先复习一下BN的理论知识：

总体来说就是先统计一个batch中的均值和方差，对输入做归一化操作，之后对其进行缩放和移位。

好的，那么理论已经具备，实际中神经网络是怎么训练和推荐的呢？如下：

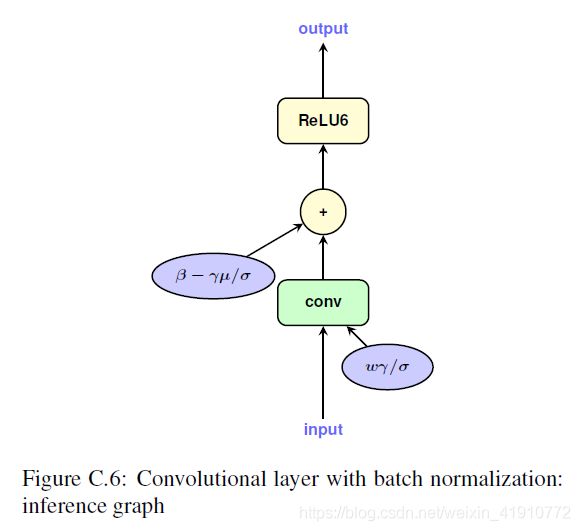
在推断时BN是和Conv结合在一起的，可达到加快运算速度的效果，具体公式如下：

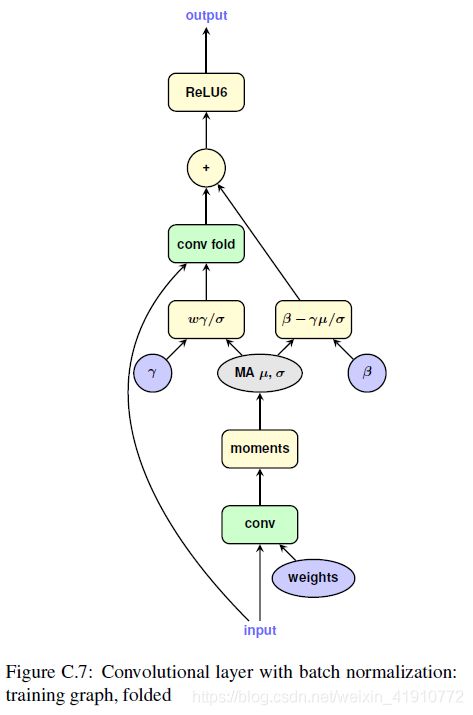
为了模拟这种效果，Google采用的方法很独特，加入了将原先的卷积和BN的基础上添加了一个卷积，共两个卷积，其中一个用于获取BN的参数，另一个用于量化后卷积。如下图：

以上两张图中都有两条通路：右侧用于卷积、BN，然后将参数都量化出来；左侧使用量化后的参数进行卷积。为了便于理解，放上一段代码：
 

def forward(self, input):
        # 训练态
        if self.training:
            # 先做普通卷积得到A，以取得BN参数
            output = F.conv2d(
                input=input,
                weight=self.weight,
                bias=self.bias,
                stride=self.stride,
                padding=self.padding,
                dilation=self.dilation,
                groups=self.groups
            )
            # 更新BN统计参数（batch和running）
            dims = [dim for dim in range(4) if dim != 1]
            batch_mean = torch.mean(output, dim=dims)
            batch_var = torch.var(output, dim=dims)
            with torch.no_grad():
                if self.first_bn == 0:
                    self.first_bn.add_(1)
                    self.running_mean.add_(batch_mean)
                    self.running_var.add_(batch_var)
                else:
                    self.running_mean.mul_(1 - self.momentum).add_(batch_mean * self.momentum)
                    self.running_var.mul_(1 - self.momentum).add_(batch_var * self.momentum)
            # BN融合
            if self.bias is not None:  
              bias = reshape_to_bias(self.beta + (self.bias -  batch_mean) * (self.gamma / torch.sqrt(batch_var + self.eps)))
            else:
              bias = reshape_to_bias(self.beta - batch_mean  * (self.gamma / torch.sqrt(batch_var + self.eps)))# b融batch
            weight = self.weight * reshape_to_weight(self.gamma / torch.sqrt(self.running_var + self.eps))     # w融running
        # 测试态
        else:
            #print(self.running_mean, self.running_var)
            # BN融合
            if self.bias is not None:
              bias = reshape_to_bias(self.beta + (self.bias - self.running_mean) * (self.gamma / torch.sqrt(self.running_var + self.eps)))
            else:
              bias = reshape_to_bias(self.beta - self.running_mean * (self.gamma / torch.sqrt(self.running_var + self.eps)))  # b融running
            weight = self.weight * reshape_to_weight(self.gamma / torch.sqrt(self.running_var + self.eps))  # w融running

        # 量化A和bn融合后的W

        if not self.first_layer:

            input = self.activation_quantizer(input)

        q_input = input

        q_weight = self.weight_quantizer(weight) 

        # 量化卷积

        if self.training:  # 训练态

          output = F.conv2d(

              input=q_input,

              weight=q_weight,

              bias=self.bias,  # 注意，这里不加bias（self.bias为None）

              stride=self.stride,

              padding=self.padding,

              dilation=self.dilation,

              groups=self.groups

          )

          # （这里将训练态下，卷积中w融合running参数的效果转为融合batch参数的效果）running ——> batch

          output *= reshape_to_activation(torch.sqrt(self.running_var + self.eps) / torch.sqrt(batch_var + self.eps))

          output += reshape_to_activation(bias)

        else:  # 测试态

          output = F.conv2d(

              input=q_input,

              weight=q_weight,
              bias=bias,  # 注意，这里加bias，做完整的conv+bn
              stride=self.stride,
              padding=self.padding,
              dilation=self.dilation,
              groups=self.groups

          )

        return output

 

 3）最大值和最小值的获取

3.3 部署

1）conv

对于单个卷积的量化部署基本已在3.1中讲过，另外补充一点，在最后需要做一步round操作，因为量化后的那个式子不是严格的等式，还是有量化误差的。

2）conv and Relu

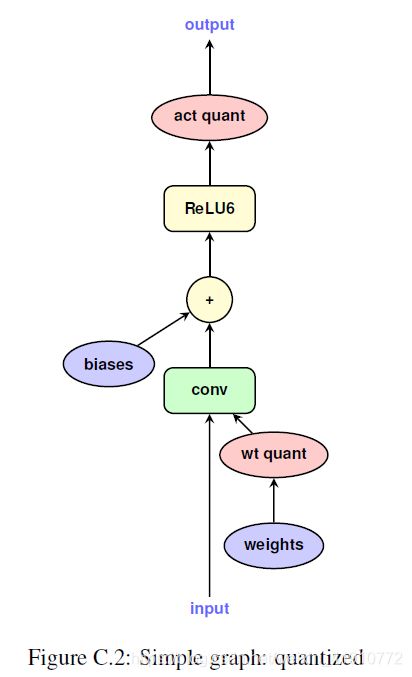
首先一般会想到：先按照3.1中的那样量化计算，之后根据zero_point做Relu激活，然而Google并不是这样使用的。
       根据3.2中的第一张图可知，在conv和relu之间没有做量化处理，为什么可以将Relu和conv结合在一起运算？可以这么理解，假设输出浮点数在[-1,1]，使用[0,255]的数值表示；结合后浮点数范围为[0,1]，也使用[0,255]表示，虽然两种情况下相同的浮点数使用不同的整形来表示（例如第一种情况浮点数0，那么在整形中使用128来表示；第二种情况的浮点数0使用0来表示），但scale和zero_point也不同，使用3.2中的公式也是可以达到目的的。为了便于理解，这里有两种表述方式：第一种，浮点数的范围不同，仅仅会导致离散化的精度不同，而计算出的大于0的数该是多少，还是多少（会有误差，但误差多少，请看第二种），小于0的数则全都等于0；第二种，可以理解为Relu和conv结合后，相当于将[-1,1]的浮点数使用[-255,255]之间，误差能看懂了吗，相比Relu和conv结合之前，精度是升高的。为什么可以将Relu和conv结合在一起运算？可以这么理解，假设输出浮点数在[-1,1]，使用[0,255]的数值表示；结合后浮点数范围为[0,1]，也使用[0,255]表示，虽然两种情况下相同的浮点数使用不同的整形来表示（例如第一种情况浮点数0，那么在整形中使用128来表示；第二种情况的浮点数0使用0来表示），但scale和zero_point也不同，使用3.2中的公式也是可以达到目的的。为了便于理解，这里有两种表述方式：第一种，浮点数的范围不同，仅仅会导致离散化的精度不同，而计算出的大于0的数该是多少，还是多少（会有误差，但误差多少，请看第二种），小于0的数则全都等于0；第二种，可以理解为Relu和conv结合后，相当于将[-1,1]的浮点数使用[-255,255]之间，误差能看懂了吗，相比Relu和conv结合之前，精度是升高的。

之前一直对论文中这句话不理解，In practice, the quantized training process (section3) tends to learn to make use of the whole output uint8 [0, 255] interval so that the activation function no longer does anything, its effect being subsumed in the clamping to [0, 255] implied in the saturating cast to uint8. 经过以上思考终于明白了，果然clamp的使用直接就可以起到Relu的作用了。

3）average_pooling

部署时是求整数的平均，可是如果整数的平均不是整数呢？这个时候可以在训练模拟部署时的运算，不是整数，可以四舍五入，所以在训练时可以对pooling之后的输入做量化，这个量化所需的最大值、最小值、scale、zero_point都是上一层输出的值，这个量化的过程就是四舍五入的过程，因此在部署时会和训练时保持一致。（可以自己构建一个module改写pool，里面包含对pool输出的量化）

四、经典论文解读之TensorRT

请转链接：TensorRT 

先发表出去，慢慢更新！！！