神经网络与深度学习-chapter1 神经网络
英语原文:Neural Networks and Deep Learning(Michael Nielsen)
中文译文:神经网络与深度学习(Michael Nielsen)
第 1 章 使用神经网络识别手写数字
1、感知机(Perceptrons)
神经网络是从感知机发展起来的,感知机在1950s和1960s由Frank Rosenblatt发明
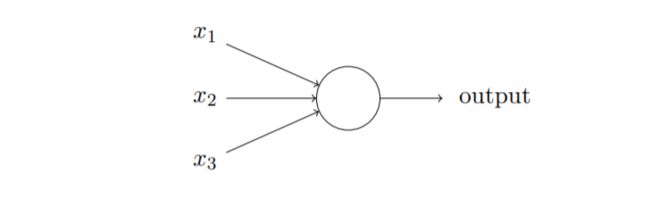
- 感知机的工作原理:一系列输入 { x 1 , x 2 , x 3 , … } \{x1, x 2, x 3, \ldots\} {x1,x2,x3,…},通过 w j x j w_jx_j wjxj加权求和与阈值 t h r e s h o l d threshold threshold比较,得到输出 o u t p u t output output,再训练各变量 x j x_j xj的权重 w j w_j wj来实现感知机的决策功能。
注:不同的权重 w w w和阈值 t h r e s h o l d threshold threshold,对应不同的决策模型,且感知机是单输出的
更精确的代数形式:
output = { 0 if ∑ j w j x j ≤ threshold 1 if ∑ j w j x j > threshold \text { output }= \begin{cases}0 & \text { if } \sum_{j} w_{j} x_{j} \leq \text { threshold } \\ 1 & \text { if } \sum_{j} w_{j} x_{j}>\text { threshold }\end{cases} output ={01 if ∑jwjxj≤ threshold if ∑jwjxj> threshold
简化 w ⋅ x w·x w⋅x = ∑ j \sum_j ∑j w j w_j wj x j x_j xj、 b b b = − t h r e s h o l d -threshold −threshold,得
output = { 0 if w ⋅ x + b ≤ 0 1 if w ⋅ x + b > 0 \text { output }= \begin{cases}0 & \text { if } w \cdot x+b \leq 0 \\ 1 & \text { if } w \cdot x+b>0\end{cases} output ={01 if w⋅x+b≤0 if w⋅x+b>0 - 将多个感知机单元并联可以得到简单神经网络(neural network),浅(深)层神经网络可以模拟简单(复杂)的非线性函数

2、Sigmoid神经元
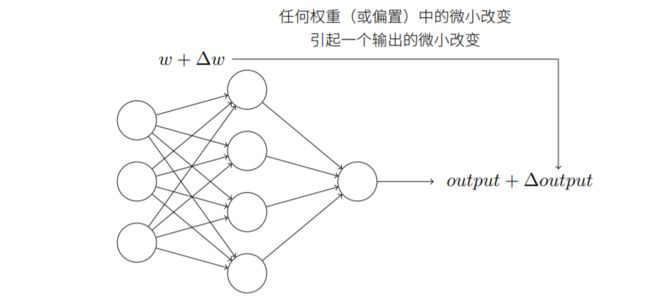
如上图所示为一个神经网络,如果权重(或偏置)的微小变化能够让输出也相应有一个比较小的变化,那么就可以让这个神经网络做一个稍微复杂一点的工作,如手写数字识别。
但当我们在神经网络中使用感知机单元时,因感知机的输出是二值(0 or 1)的,只有在阈值附近,才可能导致神经元的输出变化,而且还是突变的。
故权重或偏置的微小变化有时可能导致该感知器的输出完全“逆转”,如0变为1,这种“逆转”可能导致网络其他部分的行为变得非常复杂或难以预测,显然这和我们的期望不符。
sigmoid神经元可以用来解决这个问题,它使得网络权重和偏差的小变化仅对输出产生较小的变化。 sigmoid 函数的形式与一个sigmoid神经元的输出如下:
z ≡ w ⋅ x + b z ≡ w·x + b z≡w⋅x+b σ ( z ) ≡ 1 1 + e − z \sigma(z) ≡ \frac{1}{1+e^{-z}} σ(z)≡1+e−z1sigmoid 函数拥有一些特性:光滑可导、输出范围(0,1)、单调递增。
(可以看到sigmoid函数的输出是从 0 到 1 连续变化的,在 0 处函数值为0.5)
令 x x x为神经元的输入 ∑ j w j x j \sum_jw_j x_j ∑jwjxj,合起来就是 σ ( z ) ≡ 1 1 + exp ( − ∑ j w j x j − b ) \sigma(z) \equiv \frac{1}{1+\exp \left(-\sum_{j} w_{j} x_{j}-b\right)} σ(z)≡1+exp(−∑jwjxj−b)1
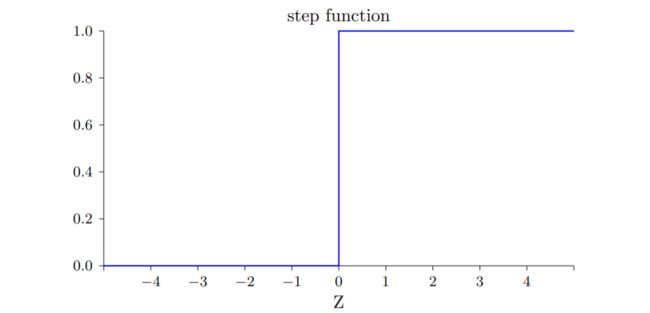
另外,改变 w , b w,b w,b的值,是可以改变曲线的形状的,具体说来, w w w越大,曲线在0处变化越陡,可以想象到当 w w w足够大时,sigmoid的输出也就只有0 和 1了,函数图像就和下面感知机一样。

感知机模型实际上是一个阶跃函数:跳跃不可导、二值{0,1}。
据sigmoid函数的输出 o u t p u t output output的微分表达式,我们可以得到下面的式子,它展现了 Δ o u t p u t \Delta output Δoutput与 Δ w \Delta w Δw, Δ b \Delta b Δb的近似线性关系,也说明了小的 Δ w \Delta w Δw, Δ b \Delta b Δb对应较小的 Δ o u t p u t \Delta output Δoutput。
Δ output ≈ ∑ j ∂ output ∂ w j Δ w j + ∂ output ∂ b Δ b \Delta \text { output } \approx \sum_{j} \frac{\partial \text { output }}{\partial w_{j}} \Delta w_{j}+\frac{\partial \text { output }}{\partial b} \Delta b Δ output ≈j∑∂wj∂ output Δwj+∂b∂ output Δb由此可知: Δ o u t p u t Δoutput Δoutput是⼀个反映权重和偏置变化——即 Δ w j Δwj Δwj和 Δ b Δb Δb的线性函数,使得选择权重 Δ w j Δwj Δwj和偏置 Δ b Δb Δb的微小变化可以达到输出 Δ o u t p u t Δoutput Δoutput的微小变化。
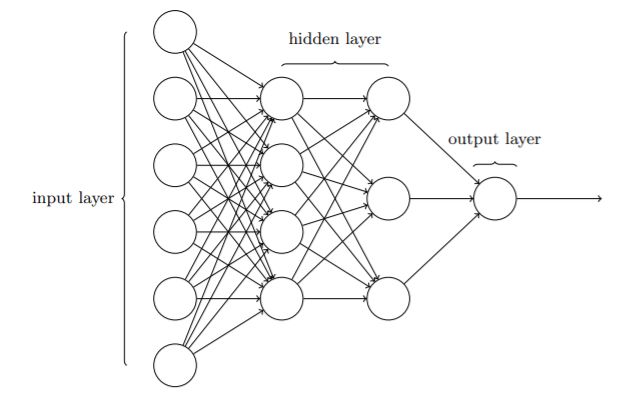
3、神经网络的结构
神经网络包括输入层、隐藏层和输出层
① 一般而言,只有一个隐藏层的神经网络被认为是简单神经网络(浅层网络),拥有多个隐藏层的神经网络被称为深度网络。
② 手写识别数据集(MNIST)是一个入门级的计算机视觉数据集,它包含各种手写数字图片及其对应的标签。
- MNIST数据分为两部分。第一部分包含60,000张图像作为训练集(train_data)。图像是灰度级的,大小为28×28像素。
- MNIST数据集的第二部分是要用作测试集(test_data)的10,000张图像,也是28×28的灰度图像。
③ 为了让机器能识别出图中的数字,需要通过算法学习。
- 我们将每一张28*28的灰质图像转换为784的一维数据作为神经网络的输入层,隐藏层用15个神经元,输出层为10个神经元。
- 因为我们的数据是0~9的图片,通过神经网络输出采用One-Hot编码(一位有效编码)的方式,即10个神经元中1个期望输入为1,其余9个为0。比如期望输出为5,则神经网络的输出层的目标输出应为(0,0,0,0,0,1,0,0,0,0)T。
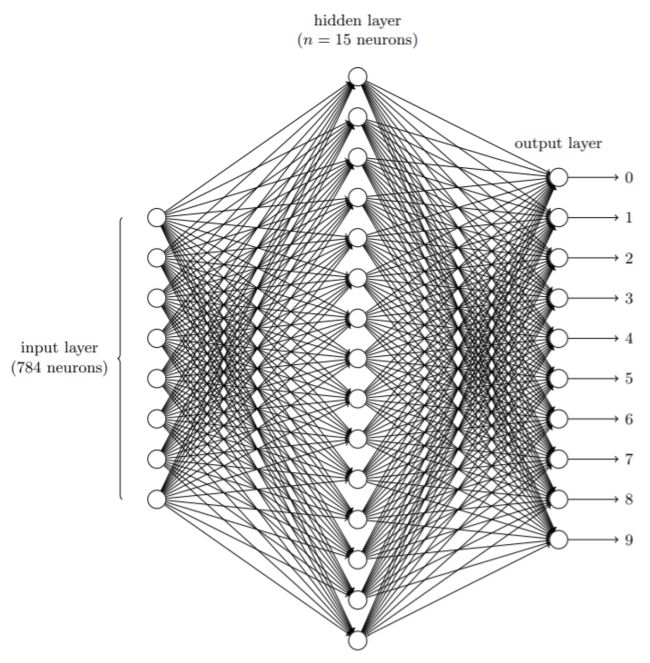
思考:为什么不用4个神经元作为输出,即以二进制表示对应数字,而是采用10个?
4、梯度下降算法
① 我们说神经网络拥有一定的智能是因为它具备一定的学习和决策能力
- 通过训练权重 w w w和偏置 b b b,神经网络可以被塑造成我们想要的滤波器
- 或训练成辨识模型(黑箱:对应X—>Y的映射关系f),训练好的模型对于新的输入就可得到模型的预测输出。
② 我们需要一个能自动学习权重和偏置的算法,使得神经网络通过更新权重或偏置,让神经网络的输出接近我们期望的输出。为此,我们先来定义损失函数(cost function),下面是一个二次损失函数(quadratic cost function),它也被称为均方误差(mean squared error)或 MSE。
C ( w , b ) ≡ 1 2 n ∑ x ∥ y ( x ) − a ∥ 2 C(w, b) \equiv \frac{1}{2 n} \sum_{x}\|y(x)-a\|^{2} C(w,b)≡2n1x∑∥y(x)−a∥2其中,w 表示所有的网络中权重的集合,b 表示所有的偏置,n 表示训练输⼊数据的个数,a 表示当输⼊为 x 时输出的真实输入,y(x)表示当输入为x时的实际输出,求和则是在总的训练输入 x 上进⾏的。
③ 我们的目标是使得损失函数 C ( w , b ) C(w,b) C(w,b)最小化。损失C是关于w和b的函数,可以通过负梯度来逐步修正权值,使损失朝着极值点的方向前进,这被称作梯度下降法(gradient descent)。
假设我们要用梯度下降法来优化一个函数 C ( v ) C(v) C(v),我们关心的是 C ( v ) C(v) C(v)在哪里取到它的全局最小值。
- 有一个很好的比喻来解释梯度下降算法。让我们想象待优化的函数是一个山谷,有一个球在山谷的斜坡上滚下来。日常经验告诉我们,球将最终滚到山谷的底部。
- 也许我们可以使用这个想法来找到函数的最小值?
我们将随机选择一个球的起点,然后模拟球滚动到山谷底部的运动。我们需要了解山谷的局部“形状”,从而知道球应该如何滚动。
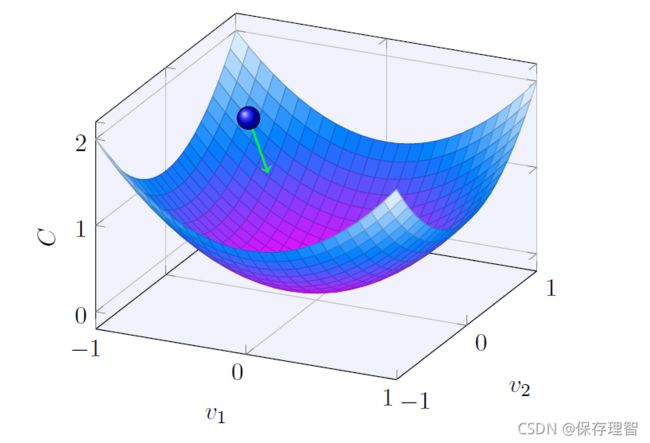
我们让球在 v 1 v1 v1上滚动 Δ v 1 Δv1 Δv1,在 v 2 v2 v2上滚动 Δ v 2 Δv2 Δv2, Δ C ΔC ΔC近似等于: Δ C ≈ ∂ C ∂ v 1 Δ v 1 + ∂ C ∂ v 2 Δ v 2 \Delta C \approx \frac{\partial C}{\partial v_{1}} \Delta v_{1}+\frac{\partial C}{\partial v_{2}} \Delta v_{2} ΔC≈∂v1∂CΔv1+∂v2∂CΔv2我们需要找到 Δ v 1 Δv1 Δv1与 Δ v 2 Δv2 Δv2使得 Δ C ΔC ΔC为负数,这样就能逐渐使球滚入谷底。为此,定义函数 C ( v ) C(v) C(v)的梯度:
∇ C ≡ ( ∂ C ∂ v 1 , ∂ C ∂ v 2 ) \nabla C \equiv\left(\frac{\partial C}{\partial v_{1}}, \frac{\partial C}{\partial v_{2}}\right) ∇C≡(∂v1∂C,∂v2∂C)则有 Δ v ≡ ( Δ v 1 , Δ v 2 ) T \Delta v \equiv\left(\Delta v_{1}, \Delta v_{2}\right)^{T} Δv≡(Δv1,Δv2)T Δ C ≈ ∇ C ⋅ Δ v \Delta C \approx \nabla C \cdot \Delta v ΔC≈∇C⋅Δv
由此当 Δ v Δv Δv取下面的形式时, Δ C ΔC ΔC定为负。其中 η η η是一个很小的正数,被称为学习率(learning rate)。 Δ v = − η ∇ C \Delta v=-\eta \nabla C Δv=−η∇C则,其中 Δ C ≥ 0 ΔC ≥ 0 ΔC≥0 Δ C ≈ − η ∇ C ⋅ ∇ C = − η ∥ ∇ C ∥ 2 \Delta C \approx-\eta \nabla C \cdot \nabla C=-\eta\|\nabla C\|^{2} ΔC≈−η∇C⋅∇C=−η∥∇C∥2由此,无论C是多少维变量的函数,通过反复应用梯度下降更新规则,就可以到达函数最小值(这是对凸函数而言,非凸函数只能保证收敛到局部最小值)。
而新位置 v ′ = v + Δ v : v' = v+Δv: v′=v+Δv: v → v ′ = v − η ∇ C v \rightarrow v^{\prime}=v-\eta \nabla C v→v′=v−η∇C对于神经网络,我们可以用下面的式子来更新权值和偏值: w k → w k ′ = w k − η ∂ C ∂ w k b l → b l ′ = b l − η ∂ C ∂ b l \begin{aligned}w_{k} \rightarrow w_{k}^{\prime} &=w_{k}-\eta \frac{\partial C}{\partial w_{k}} \\b_{l} \rightarrow b_{l}^{\prime} &=b_{l}-\eta \frac{\partial C}{\partial b_{l}}\end{aligned} wk→wk′bl→bl′=wk−η∂wk∂C=bl−η∂bl∂C实际计算中,为了计算 ∇ C \nabla C ∇C,我们需要对每个输入x计算相应的 ∇ C x \nabla C_x ∇Cx,然后取平均值求出: ∇ C = 1 n ∑ x ∇ C x \nabla C=\frac{1}{n} \sum_{x} \nabla C_{x} ∇C=n1x∑∇Cx④ 当输入数据的量很大时,这会花费很长的时间,随机梯度下降算法(stochastic gradient descent)可以用于提高学习速度。
- 思路:分批训练,即随机地从训练集中选取m个样本组成小批量数据(mini-batch) { x 1 , x 2 , … , x m } \{x1, x 2, \ldots ,x_m\} {x1,x2,…,xm},用该小批量数据的梯度变化 ∇ C m i n i \nabla C_{mini} ∇Cmini(m个x的平均梯度)来估算整个 ∇ C \nabla C ∇C(n个x的平均梯度): ∑ j = 1 m ∇ C X j m ≈ ∑ x ∇ C x n = ∇ C \frac{\sum_{j=1}^{m} \nabla C_{X_{j}}}{m} \approx \frac{\sum_{x} \nabla C_{x}}{n}=\nabla C m∑j=1m∇CXj≈n∑x∇Cx=∇C随机梯度下降算法的梯度下降更新规则如下: w k → w k ′ = w k − η m ∑ j ∂ C X j ∂ w k b l → b l ′ = b l − η m ∑ j ∂ C X j ∂ b l \begin{aligned}w_{k} \rightarrow w_{k}^{\prime}&=w_{k}-\frac{\eta}{m} \sum_{j} \frac{\partial C_{X_{j}}}{\partial w_{k}} \\b_{l}\rightarrow b_{l}^{\prime} &=b_{l}-\frac{\eta}{m} \sum_{j} \frac{\partial C_{X_{j}}}{\partial b_{l}}\end{aligned} wk→wk′bl→bl′=wk−mηj∑∂wk∂CXj=bl−mηj∑∂bl∂CXj实际代码实现过程,需要对神经网络进行多次迭代学习,每一次迭代先对训练集进行洗牌,然后选取 m m m个组成小批量数据进行训练,一直往下取 m m m个进行训练,直到到达训练集底部,如果最后一个小批量数据的样本数(训练集剩余样本数)小于 m m m,则进入下一代学习,在对训练集洗牌后,将训练集开头的若干个补全至小批量数据凑成 m m m个样本。