CS224W图神经网络笔记自用：Message passing and Node Classification

Message Passing and Node Classification

1. outline

1.1 前言

要解决的问题：给定一个在某些节点上有标签的网络，我们如何为网络中的所有其他节点分配标签（半监督节点分类问题）？

在第三章，我们采用节点嵌入的方法来解决这个问题，今天我们将讨论一个替代解决框架：消息传递，背后的思想是，网络中存在相关性（依赖性），即相似的节点是相互连接的。核心概念是collective classification（集体分类）：即将标签一起分配给网络中所有节点的想法。
今天我们将介绍三种技术：

• Relational classification（关系分类）
• Iterative classification（迭代分类）
• Correct & Smooth（正确性和平滑性）

1.2 网络中存在相关性

节点的行为在网络的链接中相互关联，相关性是指：相近的节点颜色相同（属于同一类）。

关于网络中节点行为的相关性，存在以下两种解释：

1.2 Social Homophily

同质性：个体有与相似的人交往和联系的倾向（“物以类聚”）
这种同质性已在大量基于各种属性（例如，年龄、性别、组织角色等）的网络研究中观察到：
例如，专注于同一研究领域的研究人员更有可能建立联系（在会议上开会、在学术会谈中进行互动等）。
example:在线社交网络

志趣相投的人因为同质性联系更加紧密

1.3 Social Influence

影响：社会关系可以影响一个人的个人特征

2. 如何利用网络中的节点相关性

2.1 启发点（Motivation）

• 类似节点通常在网络中紧密连接或直接连接：
  • Guilt-by-assoiation：如果我连接到带有标签X的节点，那么我很可能会带有标签X。
  • example：恶意/良性网页：
    恶意网页相互链接，以提高可见性，看起来可信，并在搜索引擎中排名更高，所以如果一个网页是恶意的，那么连接到它的网页应该也是恶意的。
• 在网络中节点v的分类标签可能取决于：
  • 节点v的特征
  • 节点v邻居的标签
  • 节点v邻居的特征

2.2 半监督学习

下面是一个半监督学习任务：



Task：根据节点特征和网络结构信息找出节点的各个标签的概率$P(Y_v)$

**集体分类（collective classification）**问题概述：

• 想法：使用相关性同时分类互连节点
• Probabilistic framework
• 马尔可夫假设：节点v的标签$Y_v$仅取决于其邻居集$N_v$的标签
  $$P(Y_v)=P(Y_v|N_v)$$
• 集体分类有三步：
  1. Local Classifier: 设置初始标签（按照节点属性，不依赖网络信息）
  2. Relational Classifier：捕获节点之间的相关性
  3. Collective Inference（集体推理）：在图中传递相关性（迭代地将关系分类器应用于每个节点并更新，以传递相关性）

应用：

• 文档分类
• 词性标记
• 链接预测
• 光学字符识别
• 图像/三维数据分割
• 传感器网络中的实体分辨率
• 垃圾邮件和欺诈检测

接下来我们将专注讨论半监督节点问题，并介绍三种解决方法：

• Relational classification（关系分类）
• Iterative classification（迭代分类）
• Correct & Smooth（正确性和平滑性）

3. Relational Classification

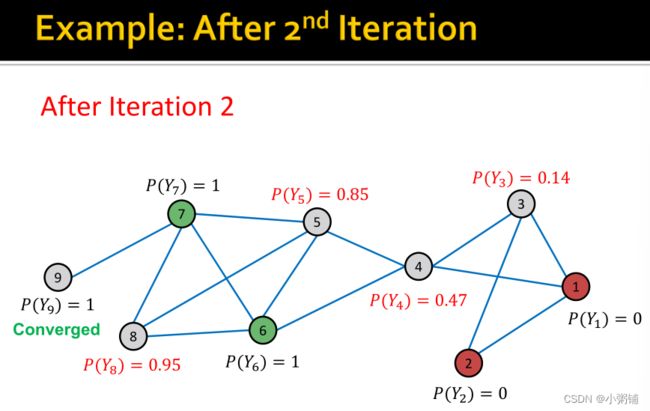
思想：在网络中传播节点标签，节点v的类概率$Y_v$是其邻居类概率的加权平均。
初始化：对于已标记的节点v，用真实的标签初始化$Y_v$；如果v未被标记，就初始化$Y_v=0.5$。以随机顺序更新所有节点，直到收敛或达到最大迭代次数。
update：用以下公式更新节点v及其标签c（例如0或1），该公式的基本假设是有边相连的节点标签相同。如果边具有强度/权重信息，$A_{v,u}$的值可以是边之间的权重，$P(Y_v=c)$是节点v具有标签c的概率。
这样做的问题在于：

• 无法保证收敛
• 模型不能利用节点的特征信息
  
  
  
  
  
  
  
  
  

4. Iterative Classification

Relational classifier没有利用节点的属性，iterative classification方法利用节点v的属性$f_v$和其邻居集$N_v$的标签$z_v$来分类节点v，我们训练两个分类器：基础分类器和关系分类器

4.1 computing the Summary $z_v$

$Z_v$是能捕获节点v周围标签的向量，我们可以用以下几种不同的方式设置$Z_v$：

• 将其设置为$N_v$中每个标签的比例
• 将其设置为$N_v$中最常见的标签
• 将其设置为$N_v$中标签的数量
  

4.2 迭代分类器的架构

阶段一：仅根据节点属性进行分类，同时在标记的训练集上，训练两个分类器（可以使用线性分类器，神经网络等方法）阶段二：迭代直至收敛。

• 在测试集上，基于分类器${\varphi }_1$设置标签$Y_v$，计算$z_v$，然后基于分类器${\varphi }_2$预测标签
• 对每个结点v重复一下过程
  • 根据所有结点$u\in N_u$的标签$Y_u$ 更新$z_v$
  • 根据新的$z_v({\varphi }_2)$更新$Y_v$
• 迭代直到类标签稳定或达到最大迭代次数
• 注意：不保证收敛

4.3 Example: Web Page Classification

根据只靠节点特征分类的基础分类器${\varphi }_1$，要预测的节点被错误分类成了类0，我们能通过网络结构信息改进这个结果吗？
接下来，我们将创建能捕获网络结构信息的向量$z_v$来改进分类结果：

$I$的第一个值$I_0$代表传入边中预测为0的节点数；
$I$的第一个值$I_1$代表传入边中预测为1的节点数
$O_0，O_1$同理

然后我们根据$f_v和z_v$训练分类器，分类器${\varphi }_1$只使用$f_v$进行训练，分类器${\varphi }_2$使用$f_v和z_v$进行训练。

5. Collective Classification: Correct & Smooth

5.1 C&S

最后，我们介绍C&S，一种最新的集体分类方法。
C&S方法在当前的OGB（节点属性预测）排行榜中名列前茅
现在我们有一个部分标记的图和图上节点的特征，我们用C&S做节点分类任务：
C&S方法有三个步骤：

• 训练基础预测器
• 使用基础预测仪预测所有节点的软标签
• 使用图结构对预测进行后期处理，以获得所有节点的最终预测

5.2 Train Base Predictor

训练预测所有节点上的软标签（类概率）的基本预测器。

• 标记节点用于测试/验证数据
• 基本预测器可以很简单：仅使用节点特征的线性模型/多层感知器（MLP）
  

5.3 Predict Over All Nodes

给定一个经过训练的基预测器，我们应用它来获得所有节点的软标签。

• 虽然我们希望这些软标签准确无误，但是事实肯定并非如此。
• 我们是否可以使用图形结构对预测进行后处理，使其更准确？

5.4 Post-Process Predictions

C&S使用两个步骤对软预测(soft predictions)进行后期处理

• Correct step
• Smooth step

Correct step: 核心思想是：我们期望基本预测中的误差沿图中的边呈正相关。换言之，节点u处的错误会增加u的相邻节点发生类似错误的概率。因此，我们应该在图表上“spread”这种不确定性。
C&S背后的思想：

• Correct step:

  • 软标签的误差程度是有偏差(biased)的
  • 我们需要纠正误差偏差。

• Smooth step:

  • 预测得到的软标签在图形上可能不平滑
  • 我们需要平滑软标签

C&S Post-Processing: Correct Step

• Correct step：
  • 计算节点的训练误差
    • 训练误差：真实标签减去软标签，未标记节点误差为0。
      
• 归一化扩散矩阵$\tilde{A}\equiv D^{-1/2}A{D}^{-1/2}$
  • $A$为邻接矩阵，$\tilde{A}$是扩散矩阵
  • $D\equiv Diag(d_1,...,d_N)$是degree matrix(度数矩阵）
  • $A_{ii}$=1。
• 所有的特征值${\lambda }^{\prime }s$都在范围[-1,1]内
  • 特征值$\lambda =1$的特征向量为$D^{1/2}1$($1$是值全为1的特征向量）
    • 证明：$\tilde{A}{D}^{-1/2}1=D^{-1/2}A{D}^{-1/2}{D}^{1/2}1=D^{-1/2}A1=D^{-1/2}D1=1\cdot D^{1/2}1$
  • $\tilde{A}$的幂（${\tilde{A}}^K$)对于任何K都是well-behaved
    • ${\tilde{A}}^K$的特征值都在[-1,1]之内
    • 最大的特征总是1
• 如果节点i和j相连，那么the weight $\tilde{A}$是$\frac{1}{\sqrt{d_i}\sqrt{d_j}}$
  • 如果i和j仅和对方相连，那么$\tilde{A}$会很大
  • 如果i和j还和其他很多节点相连，$\tilde{A}$会比较小
• 扩散训练误差：$E^{(t+1)}\leftarrow (1-\alpha )\cdot E^{(t)}+\alpha \cdot \tilde{A}{E}^{(t)}$，假设邻近节点的预测误差相近，和PageRank的迭代公式类似，$\alpha$是超参数，沿边缘扩散训练误差。假设：附近节点的误差相似

• 将缩放的扩散训练误差添加到预测的软标签中
  

• 沿图中的边平滑校正的软标签

  • 假设：邻近的节点倾向于共享相同的标签
  • 注意：对于训练节点，我们使用真实的硬标签而不是软标签
    

• Smooth step

  • 沿着图结构扩散标签$Z^{(0)}$
  • $Z^{(t+1)}\leftarrow (1-\alpha )\cdot Z^{(t)}+\alpha \cdot \tilde{A}{Z}^{(t)}$，$\tilde{A}{Z}^{(t)}$表示沿边扩散标签
    
    

• 更多细节见Zhu et al. ICML 2013
  这个示例表明，C&S使用图形结构成功地提高了基础模型的性能。
  
  

5.5 总结

• Correct&Smooth（C&S）使用图形结构对任何基础模型预测的软节点标签进行后期处理。
• 校正步骤：扩散并校正基础预测器的训练误差。
• 平滑步骤：平滑基础预测器的预测。
• C&S在半监督节点分类方面取得了很好的性能。