CS224W-6-message passing and node classification 第1部分
视频地址,课件和笔记可见官网。
http://web.stanford.edu/class/cs224w/

主要解决问题:给定一个网络,部分节点有标签,我们如何预测其它节点的标签。
例子:反欺诈案例,一些节点是欺诈者,一些节点是合法客户,我们怎么找到其它的欺诈者和合法客户。
补充:
图算法应用的任务有:
1、node focused,以节点为主体,预测节点的标签等,比如上面的反欺诈的例子;
2、edge focused,以边为主体,预测边的标签,比如推荐系统中 用户与商品是否发生关联(即用户是否购买商品),对这种关联关系是否发生进行预测;
3、graph focused,以整个图为主题,预测图的标签等,比如化学分子的类别预测,整个化学分子是一副完整的图,其节点是不同的化学原子;
这节课主要讲节点分类的问题,也是目前图算法应用较多的领域,我们熟悉的gcn就是属于解决node focused任务的gnn的变体结构之一。

很多时候半监督和有监督问题的定义界限模棱两可,这里之所以称之为半监督,主要是因为获取的有标签的节点数量非常稀少,所以希望通过半监督的方法来处理,如果有标签节点的数量非常多,其实用有监督也可以。

因为图的特殊性,所以这里的思路是利用网络的相似性来给所有样本进行打标,使用了红绿蓝下面三种方案。
分别是关系分类、迭代分类、信仰传播,先进程度依次递进,下面从最简单的关系分类讲起。
这里距了一个社交网络的例子来说明为什么网络结构存在相关性。
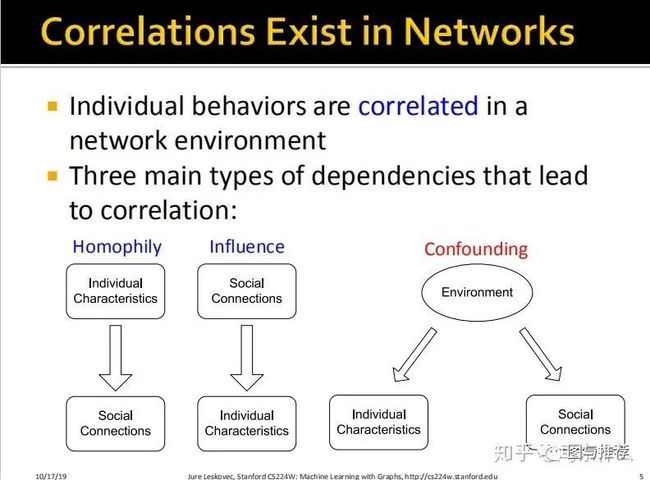
个体行为在网络环境中是相互关联的;
导致相关性的三种主要原因:
1、同质性:个体的不同特征会导致社交过程中的connection,比如相似的年龄、工作、种族、宗教信仰等会导致相似的一批人发生social connections;
2、影响力:可以看到,人的社交关系social connections反过来还会影响到个体的特征,所谓近朱者赤近墨者黑。
3、其它令人困惑的原因来自于环境environment,前面的两种是已知的能够左右人的社交关系和个人特征的重要原因之二,但是实际上还有其它的原因,这里统一归结为环境因素,例如在暴力的环境成长下的儿童成年后可能个人心里会有一定的扭曲,这同样会很重要的影响到他的社交行为和个体特征的形成。
不过大部分时候,前两者足够产生较为强大的网络相关性了,毕竟大部分人不会受到极端的环境的影响。。。

关于同质性和影响力的一些案例(讲了一些关于这类研究很成熟很全面之类的,感觉没什么价值,就不写了)

facebook的社交网络图,注释入原图,很有意思的一张图。
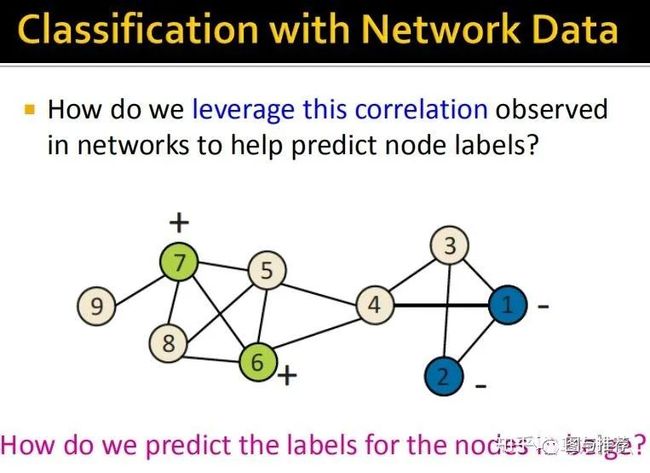
那么我们如何利用这种相关性来预测无标签的节点,上图中米色的节点为无标签的;

如何确定标签,一个naive的思路就是——一丘之貉,你和label X的人相关联则你也可能是label为X的人。下面举了一个例子:在搜索引擎中,有一些恶意网站会大量互相关联从而提高自己在搜索引擎中的排名(早期google的搜索引擎是根据网页的链接数量来排名的貌似,《数学之美》里面有提到过感兴趣的可以看看),后来,pagerank的出现很好的改善了这些问题。

未知样本的标签取决于:
1、这个未知样本O的特征;
2、这个未知样本O的相邻节点;
3、这个未知样本O的相邻节点的特征;
实际上如果仅仅考虑第一个条件就回到了我们传统的机器学习算法的范畴里了;
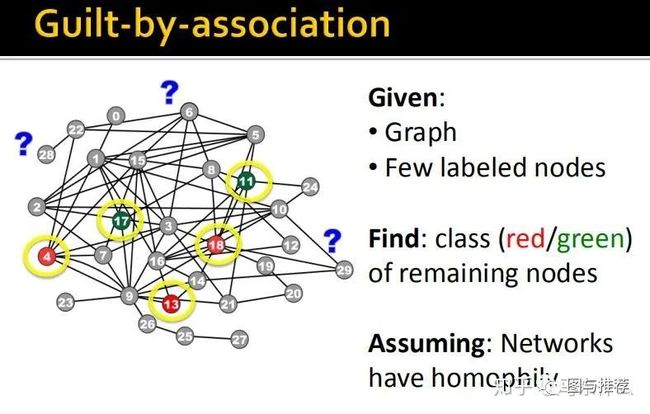

假设我们存在上面的一个巨大的网络数据,我们用n*n的W(邻接矩阵:使用二维矩阵表示这个网络图,常见的图数据的表示形式之一),假设标签为1,-1,0,分别表示正节点,负节点和无标签节点,我们首先的目标是预测哪些无标签节点可能是正节点;

利用相似性来进行分类的应用包括上述的这些。

马尔可夫假设,节点的标签取决于其邻节点的标签,实施 collective classification(翻译过来叫 集体分类。。)
具体分为三个步骤:
1、有标签样本训练分类器然后对无标签样本进行估计得到伪标签;
2、获取不同节点之间的相关性;
3、通过网络传播这些相关性;
4、不断迭代,直到收敛

首先是local classifier,就是一个标准的机器学习分类问题,不使用到网络的信息,仅仅是基于节点的特征进行分类的,说白了就是一个节点代表一个样本,这个节点的属性就是样本的特征列,然后我们可以使用lr、gbdt之类的算法来求解这个二分类问题。
(这里学生问了一个大部分初学者都会问的问题,貌似我们通过第一步就可以得到一个分类器用于预测无标签的节点,实际上如果节点的特征能够提供足够好的模型来进行预测,我们确实不太需要再深入了,问题是很多时候仅仅使用节点特征训练的模型效果一般甚至比较差,这个时候就要考虑到使用网络信息来对原始特征进行有力的补充或代替。)
然后训练一个relational classifier,使用样本的邻节点的标签和(或)特征来预测这个样本的标签,因为上一步生成了伪标签了所以此时所有节点都有标签了;
最后是实施集体学习,使用relational classifier预测每个节点的标签,这样我们会得到一批新的标签,然后再重新训练relational classifier,一直迭代到相邻节点之间的不一致性最小化(这里后面讲述的实际上是 预测的概率值不在发生变动或者变动很小的时候或者是到达了指定的迭代次数),网络的结构对于最终训练出来的模型的影响是很大的。
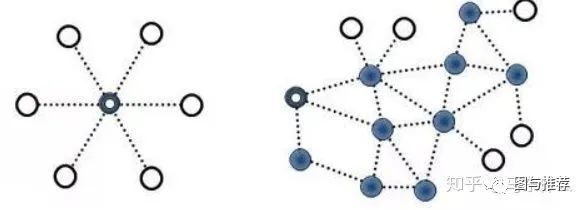
例如你在左图训练出来的概率结果会受到中心点标签的重大影响,而右图相对均匀的图结构则互相之间的影响比较平均;
实际上思路非常类似于半监督中的self-training。

这里谈到了精确推断和近似推断的问题,因为上面的步骤看起来不太靠谱,略随意的样子,为什么不进行精确推断,因为精确推断只能适用于极少的条件下,比如上面的例子,标签太少,不可能实施精确推断,除此之后精确推断对于任意结构的网络是一个np-hard的问题,也就是没有精确的解。因此我们使用近似推断来代替精确推断。
好消息是这种近似推断的做法大部分时候运行良好。

回到之前的问题,给定节点属性(特征)和小部分标签,如何预测无标签样本的标签。
下面开始正式介绍第一种方法,relational classifier

基本假设是,节点的预测概率值是其邻节点的预测概率值的加权平均。
对于有标签样本,使用真实标签进行初始化,对于无标签样本,统一0.5初始化(这里学生问了另一个问题可不可以使用别的初始化方案,答案是可以,如果有先验知识对某些标签的把握更大可以赋予更大的初始概率值,只不过使用0.5初始化比较简单而已);
然后不断随机(不一定使用随机更新的策略,但是记住不同的更新策略会影响最终的结果,再在大型的图上,使用随机更新的策略常常就足够好了)更新所有节点的预测概率值直到收敛(预测概率整体不再变化或者变换很小)或者达到指定的最大迭代次数。

这里课件和视频上的不一样,不过显然课件是正确的,因为如果按照原始视频中公式的分母使用Ni即第i个节点的邻节点的数量之和,则默认权重为1,那么和后面的权重项对不上,自相矛盾。
那么这里的思路就很直接了,随机初始化之后,我们不断使用上面的公式对节点的概率值进行更新,直到收敛为止,其中Wij表示节点i和节点j之间的边的权重,以社交网络为例,如果用户i和j之间的互动频繁则权重就更大。
但是这种方法的问题在于:
1、无法保证一定能收敛(就是可能收敛也可能不收敛)(这里讲课的大佬给了一个经验法则,如果不收敛,但是随着时间的推移,不收敛的程度没有变大而是周期性的变动,那么这个时候我们也可以结束迭代)
2、模型仅仅使用的是节点的标签信息,但是没有用到节点的属性信息(特征);
下面给了一个很详细的过程:
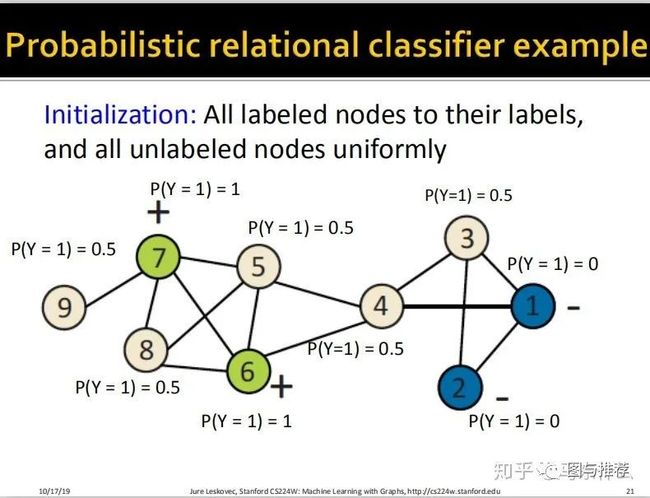




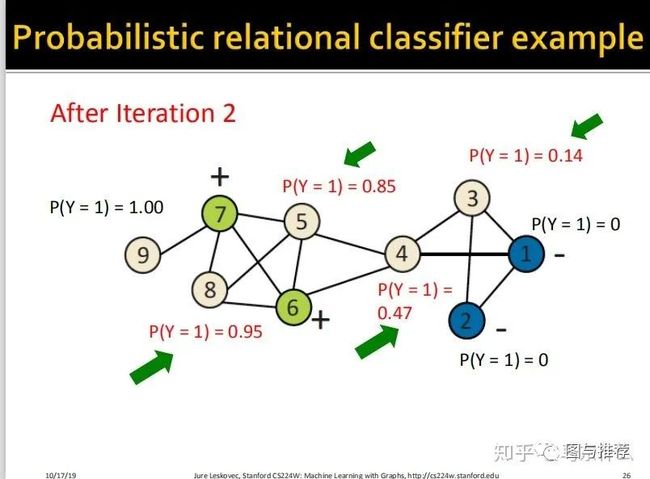

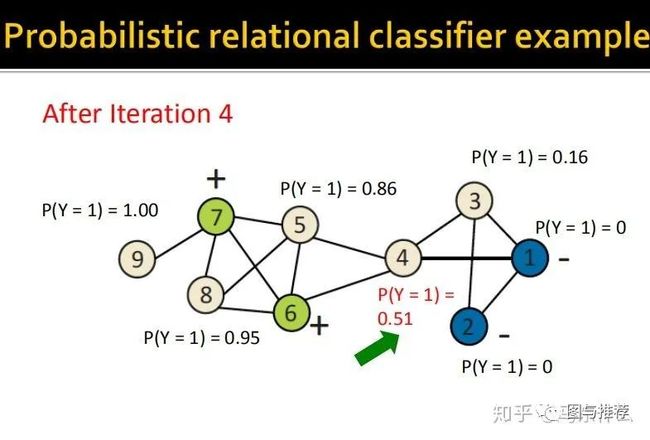
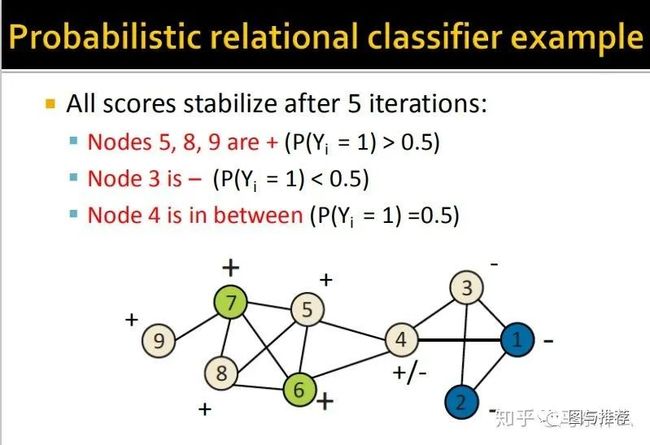
举例子永远是对于初学者来说最快的理解方式之一,这样一看对整个算法的逻辑就非常清楚了。。。
最终,经过5此迭代,预测的结果不再发生变化了,可以发现,最终的结果非常符合人类的直观认知,左侧都是正样本,因为他们看起来属于一个团体结构,右边属于负样本,他们看起来形成了一个小团体,中间的连接点4则无法判断,概率在0.5左右,从人类的理解上来说也是合理的,处于中间比较尴尬的位置。