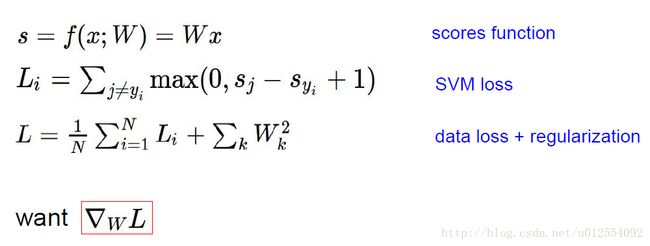CS231n学习笔记--4.Backpropagation and Neural Networks
1.损失函数
其中SVM损失函数计算的是不正确分类的得分惩罚,即Syi是正确分类结果的得分,Sj是错误分类结果的得分,超参数(1)度量正确分类得分的优越性。
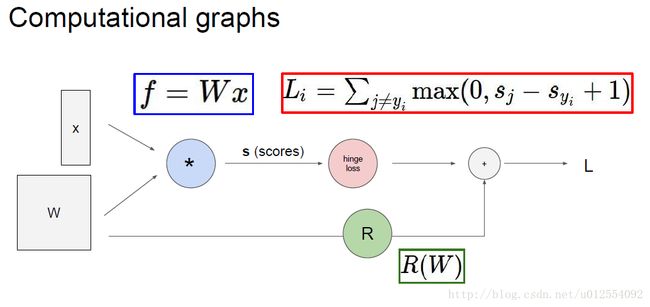
2.简单损失函数流程图:
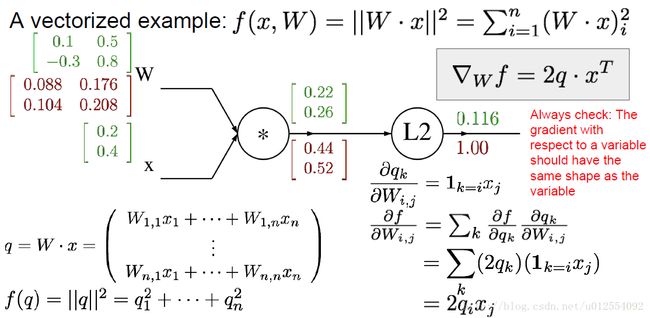
3.求解损失函数的梯度矩阵
其中,绿色数值代表前向网络中的实际值,红色数值代表反向神经网络得到的梯度值。
4.常见的激活函数
sigmoid
有点落伍了(fallen out of favor and it is rarely ever used)
原因 1:梯度饱和问题(sigmoid saturate and kill gradients),即如果神经元的激活值很大,返回的梯度几乎为零,因此反向传播的时候,也会阻断(or kill)从此处流动的梯度。此外初始化的时候,也要注意,如果梯度很大的话,也很容易造成梯度饱和。
原因 2:sigmoid outputs are not zero-centered,因为输出结果在 [0,1] 之间,都是整数,所以造成了某些维度一直更新正的梯度,某些则相反。就会造成 zig-zagging 形状的参数更新。不过利用批随机梯度下降法就会缓解这个问题,没有第一个问题严重。
tanh
很明显,tanh(non-linearity )虽然也有梯度饱和问题,但是起码是 zero-centered,因此实际中比 sigmoid 效果更好。
ReLU
好处:能够加速收敛速度,据说是因为线性,非饱和(non-saturating)的形式;运算(oprations)很实现都很简单,不用指数(exponentials)操作。
坏处:很脆弱(fragile),容易死掉(die),即如果很大的梯度经过神经元,那么就会造成此神经元不会再对任何数据点有激活。不过学习率设置小一点就不会有太大的问题。
Leaky ReLU
不是单纯的把负数置零,而是加一个很小的 slope,比如 0.01
f(x)=1(x<0)(αx)+1(x≥0)(x)。这样做是为了修复 “dying ReLU的 问题。
如果 α 作为参数,即每个神经元的 slope 都不一样,如果可以自学习的话,称为 PReLU。
Maxout
每个神经元会有两个权重,激活函数为 max(wT1x+b1,wT2+b2)
当 w1=b1=0 时,就是 ReLU
虽然和 ReLU 一样没有梯度饱和问题,也没有 dying ReLU 问题,但是参数确实原来的两倍
实践中,用 ReLU 较多,学习率要调小一点,如果 dead units 很多的话,用 PReLU 或者 Maxout 试一下。
5.minbath
深度学习的优化算法,说白了就是梯度下降。每次的参数更新有两种方式。
第一种,遍历全部数据集算一次损失函数,然后算函数对各个参数的梯度,更新梯度。这种方法每更新一次参数都要把数据集里的所有样本都看一遍,计算量开销大,计算速度慢,不支持在线学习,这称为Batch gradient descent,批梯度下降。
另一种,每看一个数据就算一下损失函数,然后求梯度更新参数,这个称为随机梯度下降,stochastic gradient descent。这个方法速度比较快,但是收敛性能不太好,可能在最优点附近晃来晃去,hit不到最优点。两次参数的更新也有可能互相抵消掉,造成目标函数震荡的比较剧烈。
为了克服两种方法的缺点,现在一般采用的是一种折中手段,mini-batch gradient decent,小批的梯度下降,这种方法把数据分为若干个批,按批来更新参数,这样,一个批中的一组数据共同决定了本次梯度的方向,下降起来就不容易跑偏,减少了随机性。另一方面因为批的样本数与整个数据集相比小了很多,计算量也不是很大。
6.Assinment 1:
参考博客:cs231n 课程作业 Assignment 1
KNN分类器
import numpy as np
class KNearestNeighbor(object):
""" a kNN classifier with L2 distance """
def __init__(self):
pass
def train(self, X, y):
"""
Train the classifier. For k-nearest neighbors this is just
memorizing the training data.
Inputs:
- X: A numpy array of shape (num_train, D) containing the training data
consisting of num_train samples each of dimension D.
- y: A numpy array of shape (N,) containing the training labels, where
y[i] is the label for X[i].
"""
self.X_train = X
self.y_train = y
def predict(self, X, k=1, num_loops=0):
"""
Predict labels for test data using this classifier.
Inputs:
- X: A numpy array of shape (num_test, D) containing test data consisting
of num_test samples each of dimension D.
- k: The number of nearest neighbors that vote for the predicted labels.
- num_loops: Determines which implementation to use to compute distances
between training points and testing points.
Returns:
- y: A numpy array of shape (num_test,) containing predicted labels for the
test data, where y[i] is the predicted label for the test point X[i].
"""
if num_loops == 0:
dists = self.compute_distances_no_loops(X)
elif num_loops == 1:
dists = self.compute_distances_one_loop(X)
elif num_loops == 2:
dists = self.compute_distances_two_loops(X)
else:
raise ValueError('Invalid value %d for num_loops' % num_loops)
return self.predict_labels(dists, k=k)
def compute_distances_two_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a nested loop over both the training data and the
test data.
Inputs:
- X: A numpy array of shape (num_test, D) containing test data.
Returns:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
is the Euclidean distance between the ith test point and the jth training
point.
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in xrange(num_test):
for j in xrange(num_train):
#####################################################################
# TODO: #
# Compute the l2 distance between the ith test point and the jth #
# training point, and store the result in dists[i, j]. You should #
# not use a loop over dimension. #
#####################################################################
pass
dists[i][j] = np.sum((X[i] - self.X_train[j]) ** 2)
#####################################################################
# END OF YOUR CODE #
#####################################################################
return dists
def compute_distances_one_loop(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a single loop over the test data.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in xrange(num_test):
#######################################################################
# TODO: #
# Compute the l2 distance between the ith test point and all training #
# points, and store the result in dists[i, :]. #
#######################################################################
pass
dists[i] = np.sum((self.X_train - X[i]) ** 2, 1)
#######################################################################
# END OF YOUR CODE #
#######################################################################
return dists
def compute_distances_no_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using no explicit loops.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
#########################################################################
# TODO: #
# Compute the l2 distance between all test points and all training #
# points without using any explicit loops, and store the result in #
# dists. #
# #
# You should implement this function using only basic array operations; #
# in particular you should not use functions from scipy. #
# #
# HINT: Try to formulate the l2 distance using matrix multiplication #
# and two broadcast sums. #
#########################################################################
pass
dists += np.sum(self.X_train ** 2, axis=1).reshape(1, num_train)
dists += np.sum(X ** 2, axis=1).reshape(num_test, 1) # reshape for broadcasting
dists -= 2 * np.dot(X, self.X_train.T)
#########################################################################
# END OF YOUR CODE #
#########################################################################
return dists
def predict_labels(self, dists, k=1):
"""
Given a matrix of distances between test points and training points,
predict a label for each test point.
Inputs:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
gives the distance betwen the ith test point and the jth training point.
Returns:
- y: A numpy array of shape (num_test,) containing predicted labels for the
test data, where y[i] is the predicted label for the test point X[i].
"""
num_test = dists.shape[0]
y_pred = np.zeros(num_test)
for i in xrange(num_test):
# A list of length k storing the labels of the k nearest neighbors to
# the ith test point.
closest_y = []
#########################################################################
# TODO: #
# Use the distance matrix to find the k nearest neighbors of the ith #
# testing point, and use self.y_train to find the labels of these #
# neighbors. Store these labels in closest_y. #
# Hint: Look up the function numpy.argsort. #
#########################################################################
pass
closest_y = self.y_train[np.argsort(dists[i])[0:k]]
#########################################################################
# TODO: #
# Now that you have found the labels of the k nearest neighbors, you #
# need to find the most common label in the list closest_y of labels. #
# Store this label in y_pred[i]. Break ties by choosing the smaller #
# label. #
#########################################################################
pass
# to find the most common element in list, you can use np.bincount
y_pred[i] = np.bincount(closest_y).argmax()
#########################################################################
# END OF YOUR CODE #
#########################################################################
return y_pred前向/后向神经网络
a.损失函数为SVM:
Python代码:
import numpy as np
#from random import shuffle
def svm_loss_naive(W, X, y, reg):
"""
Structured SVM loss function, naive implementation (with loops).
Inputs have dimension D, there are C classes, and we operate on minibatches
of N examples.
Inputs:
- W: A numpy array of shape (D, C) containing weights.
- X: A numpy array of shape (N, D) containing a minibatch of data.
- y: A numpy array of shape (N,) containing training labels; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) regularization strength
Returns a tuple of:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
"""
dW = np.zeros(W.shape) # initialize the gradient as zero
# compute the loss and the gradient
num_classes = W.shape[1]
num_train = X.shape[0]
loss = 0.0
for i in xrange(num_train):
scores = X[i].dot(W)
correct_class_score = scores[y[i]]
for j in xrange(num_classes):
if j == y[i]:
continue
margin = scores[j] - correct_class_score + 1 # note delta = 1
if margin > 0:
loss += margin
dW[:, j] += X[i]
dW[:, y[i]] -= X[i]
# Right now the loss is a sum over all training examples, but we want it
# to be an average instead so we divide by num_train.
loss /= num_train
dW /= num_train
# Add regularization to the loss.
loss += 0.5 * reg * np.sum(W * W)
dW += reg * W
#############################################################################
# TODO: #
# Compute the gradient of the loss function and store it dW. #
# Rather that first computing the loss and then computing the derivative, #
# it may be simpler to compute the derivative at the same time that the #
# loss is being computed. As a result you may need to modify some of the #
# code above to compute the gradient. #
#############################################################################
return loss, dW
def svm_loss_vectorized(W, X, y, reg):
"""
Structured SVM loss function, vectorized implementation.
Inputs and outputs are the same as svm_loss_naive.
"""
loss = 0.0
dW = np.zeros(W.shape) # initialize the gradient as zero
#############################################################################
# TODO: #
# Implement a vectorized version of the structured SVM loss, storing the #
# result in loss. #
#############################################################################
pass
N = X.shape[0]
#scores = np.dot(X, W)
#margin = scores - scores[range(0, N), y].reshape(N, 1) + 1
#margin[range(0, N), y] = 0
#margin = margin * (margin > 0) # max(0, s_j - s_yi + delta)
#loss += np.sum(margin) / N + 0.5 * reg * np.sum(W * W)
scores = X.dot(W) # N x C
margin = scores - scores[range(0,N), y].reshape(-1, 1) + 1 # N x C
margin[range(N), y] = 0
margin = (margin > 0) * margin
loss += margin.sum() / N
loss += 0.5 * reg * np.sum(W * W)
#############################################################################
# END OF YOUR CODE #
#############################################################################
#############################################################################
# TODO: #
# Implement a vectorized version of the gradient for the structured SVM #
# loss, storing the result in dW. #
# #
# Hint: Instead of computing the gradient from scratch, it may be easier #
# to reuse some of the intermediate values that you used to compute the #
# loss. #
#############################################################################
pass
counts = (margin > 0).astype(int)
counts[range(N), y] = - np.sum(counts, axis = 1)
dW += np.dot(X.T, counts) / N + reg * W
#############################################################################
# END OF YOUR CODE #
#############################################################################
return loss, dWb.损失函数为Softmax:
(不同之处仅在损失函数及其梯度计算部分):

python代码:
import numpy as np
#from random import shuffle
def softmax_loss_naive(W, X, y, reg):
"""
Softmax loss function, naive implementation (with loops)
Inputs have dimension D, there are C classes, and we operate on minibatches
of N examples.
Inputs:
- W: A numpy array of shape (D, C) containing weights.
- X: A numpy array of shape (N, D) containing a minibatch of data.
- y: A numpy array of shape (N,) containing training labels; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) regularization strength
Returns a tuple of:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
"""
# Initialize the loss and gradient to zero.
loss = 0.0
dW = np.zeros_like(W)
#############################################################################
# TODO: Compute the softmax loss and its gradient using explicit loops. #
# Store the loss in loss and the gradient in dW. If you are not careful #
# here, it is easy to run into numeric instability. Don't forget the #
# regularization! #
#############################################################################
pass
N, C = X.shape[0], W.shape[1]
for i in range(N):
f = np.dot(X[i], W)
f -= np.max(f) # f.shape = C
loss = loss + np.log(np.sum(np.exp(f))) - f[y[i]]
dW[:, y[i]] -= X[i]
s = np.exp(f).sum()
for j in range(C):
dW[:, j] += np.exp(f[j]) / s * X[i]
loss = loss / N + 0.5 * reg * np.sum(W * W)
dW = dW / N + reg * W
#############################################################################
# END OF YOUR CODE #
#############################################################################
return loss, dW
def softmax_loss_vectorized(W, X, y, reg):
"""
Softmax loss function, vectorized version.
Inputs and outputs are the same as softmax_loss_naive.
"""
# Initialize the loss and gradient to zero.
loss = 0.0
dW = np.zeros_like(W)
#############################################################################
# TODO: Compute the softmax loss and its gradient using no explicit loops. #
# Store the loss in loss and the gradient in dW. If you are not careful #
# here, it is easy to run into numeric instability. Don't forget the #
# regularization! #
#############################################################################
pass
N = X.shape[0]
f = np.dot(X, W) # f.shape = N, C
f -= f.max(axis = 1).reshape(N, 1)
s = np.exp(f).sum(axis = 1)
loss = np.log(s).sum() - f[range(N), y].sum()
counts = np.exp(f) / s.reshape(N, 1)
counts[range(N), y] -= 1
dW = np.dot(X.T, counts)
loss = loss / N + 0.5 * reg * np.sum(W * W)
dW = dW / N + reg * W
#############################################################################
# END OF YOUR CODE #
#############################################################################
return loss, dW
简单的两层网络:
步骤:
1。设置learning_rate, learning_rate_decay(每个epoch(数据集)训练后learning_rate下降的倍率,因为越训练到后面学习率应该越低,以防止震荡), num_iters,batch_size。
2。根据随机梯度下降法随机从epoch中抽取batch_size个训练样本。
3。根据batch_size个训练样本计算各中间变量(w,b…)的梯度,并根据学习率更新这些中间变量。
4。如果一个epoch训练结束,更新学习率进行下一个epoch的训练。
import numpy as np
#import matplotlib.pyplot as plt
class TwoLayerNet(object):
"""
A two-layer fully-connected neural network. The net has an input dimension of
N, a hidden layer dimension of H, and performs classification over C classes.
We train the network with a softmax loss function and L2 regularization on the
weight matrices. The network uses a ReLU nonlinearity after the first fully
connected layer.
In other words, the network has the following architecture:
input - fully connected layer - ReLU - fully connected layer - softmax
The outputs of the second fully-connected layer are the scores for each class.
"""
def __init__(self, input_size, hidden_size, output_size, std=1e-4):
"""
Initialize the model. Weights are initialized to small random values and
biases are initialized to zero. Weights and biases are stored in the
variable self.params, which is a dictionary with the following keys:
W1: First layer weights; has shape (D, H)
b1: First layer biases; has shape (H,)
W2: Second layer weights; has shape (H, C)
b2: Second layer biases; has shape (C,)
Inputs:
- input_size: The dimension D of the input data.
- hidden_size: The number of neurons H in the hidden layer.
- output_size: The number of classes C.
"""
self.params = {}
self.params['W1'] = std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def loss(self, X, y=None, reg=0.0):
"""
Compute the loss and gradients for a two layer fully connected neural
network.
Inputs:
- X: Input data of shape (N, D). Each X[i] is a training sample.
- y: Vector of training labels. y[i] is the label for X[i], and each y[i] is
an integer in the range 0 <= y[i] < C. This parameter is optional; if it
is not passed then we only return scores, and if it is passed then we
instead return the loss and gradients.
- reg: Regularization strength.
Returns:
If y is None, return a matrix scores of shape (N, C) where scores[i, c] is
the score for class c on input X[i].
If y is not None, instead return a tuple of:
- loss: Loss (data loss and regularization loss) for this batch of training
samples.
- grads: Dictionary mapping parameter names to gradients of those parameters
with respect to the loss function; has the same keys as self.params.
"""
# Unpack variables from the params dictionary
W1, b1 = self.params['W1'], self.params['b1']
W2, b2 = self.params['W2'], self.params['b2']
N, D = X.shape
# Compute the forward pass
scores = None
#############################################################################
# TODO: Perform the forward pass, computing the class scores for the input. #
# Store the result in the scores variable, which should be an array of #
# shape (N, C). #
#############################################################################
pass
hidden_layer = np.maximum(0, np.dot(X, W1) + b1)
scores = np.dot(hidden_layer, W2) + b2
#############################################################################
# END OF YOUR CODE #
#############################################################################
# If the targets are not given then jump out, we're done
if y is None:
return scores
# Compute the loss
loss = None
#############################################################################
# TODO: Finish the forward pass, and compute the loss. This should include #
# both the data loss and L2 regularization for W1 and W2. Store the result #
# in the variable loss, which should be a scalar. Use the Softmax #
# classifier loss. So that your results match ours, multiply the #
# regularization loss by 0.5 #
#############################################################################
pass
f = scores - np.max(scores, axis = 1, keepdims = True)#负值化
loss = -f[range(N), y].sum() + np.log(np.exp(f).sum(axis = 1)).sum()
loss = loss / N + 0.5 * reg * (np.sum(W1 * W1) + np.sum(W2 * W2))
#############################################################################
# END OF YOUR CODE #
#############################################################################
# Backward pass: compute gradients
grads = {}
#############################################################################
# TODO: Compute the backward pass, computing the derivatives of the weights #
# and biases. Store the results in the grads dictionary. For example, #
# grads['W1'] should store the gradient on W1, and be a matrix of same size #
#############################################################################
pass
dscore = np.exp(f) / np.exp(f).sum(axis = 1, keepdims = True)
dscore[range(N), y] -= 1
dscore /= N
grads['W2'] = np.dot(hidden_layer.T, dscore) + reg * W2
grads['b2'] = np.sum(dscore, axis = 0)
dhidden = np.dot(dscore, W2.T)
dhidden[hidden_layer <= 0.00001] = 0
grads['W1'] = np.dot(X.T, dhidden) + reg * W1
grads['b1'] = np.sum(dhidden, axis = 0)
#############################################################################
# END OF YOUR CODE #
#############################################################################
return loss, grads
def train(self, X, y, X_val, y_val,
learning_rate=1e-3, learning_rate_decay=0.95,
reg=1e-5, num_iters=100,
batch_size=200, verbose=False):
"""
Train this neural network using stochastic gradient descent.
Inputs:
- X: A numpy array of shape (N, D) giving training data.
- y: A numpy array f shape (N,) giving training labels; y[i] = c means that
X[i] has label c, where 0 <= c < C.
- X_val: A numpy array of shape (N_val, D) giving validation data.
- y_val: A numpy array of shape (N_val,) giving validation labels.
- learning_rate: Scalar giving learning rate for optimization.
- learning_rate_decay: Scalar giving factor used to decay the learning rate
after each epoch.
- reg: Scalar giving regularization strength.
- num_iters: Number of steps to take when optimizing.
- batch_size: Number of training examples to use per step.
- verbose: boolean; if true print progress during optimization.
"""
num_train = X.shape[0]
iterations_per_epoch = max(num_train / batch_size, 1)
# Use SGD to optimize the parameters in self.model
loss_history = []
train_acc_history = []
val_acc_history = []
for it in xrange(num_iters):
X_batch = None
y_batch = None
#########################################################################
# TODO: Create a random minibatch of training data and labels, storing #
# them in X_batch and y_batch respectively. #
#########################################################################
pass
indices = np.random.choice(num_train, batch_size, replace=True)
X_batch = X[indices]
y_batch = y[indices]
#########################################################################
# END OF YOUR CODE #
#########################################################################
# Compute loss and gradients using the current minibatch
loss, grads = self.loss(X_batch, y=y_batch, reg=reg)
loss_history.append(loss)
#########################################################################
# TODO: Use the gradients in the grads dictionary to update the #
# parameters of the network (stored in the dictionary self.params) #
# using stochastic gradient descent. You'll need to use the gradients #
# stored in the grads dictionary defined above. #
#########################################################################
pass
self.params['W1'] -= learning_rate * grads['W1']
self.params['b1'] -= learning_rate * grads['b1']
self.params['W2'] -= learning_rate * grads['W2']
self.params['b2'] -= learning_rate * grads['b2']
#########################################################################
# END OF YOUR CODE #
#########################################################################
if verbose and it % 100 == 0:
print 'iteration %d / %d: loss %f' % (it, num_iters, loss)
# Every epoch, check train and val accuracy and decay learning rate.
if it % iterations_per_epoch == 0:
# Check accuracy
train_acc = (self.predict(X_batch) == y_batch).mean()
val_acc = (self.predict(X_val) == y_val).mean()
train_acc_history.append(train_acc)
val_acc_history.append(val_acc)
# Decay learning rate
learning_rate *= learning_rate_decay
return {
'loss_history': loss_history,
'train_acc_history': train_acc_history,
'val_acc_history': val_acc_history,
}
def predict(self, X):
"""
Use the trained weights of this two-layer network to predict labels for
data points. For each data point we predict scores for each of the C
classes, and assign each data point to the class with the highest score.
Inputs:
- X: A numpy array of shape (N, D) giving N D-dimensional data points to
classify.
Returns:
- y_pred: A numpy array of shape (N,) giving predicted labels for each of
the elements of X. For all i, y_pred[i] = c means that X[i] is predicted
to have class c, where 0 <= c < C.
"""
y_pred = None
###########################################################################
# TODO: Implement this function; it should be VERY simple! #
###########################################################################
pass
W1, b1 = self.params['W1'], self.params['b1']
W2, b2 = self.params['W2'], self.params['b2']
hidden_layer = np.maximum(0, np.dot(X, W1) + b1)
scores = np.dot(hidden_layer, W2) + b2
y_pred = np.argmax(scores, axis = 1)
###########################################################################
# END OF YOUR CODE #
###########################################################################
return y_pred