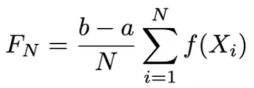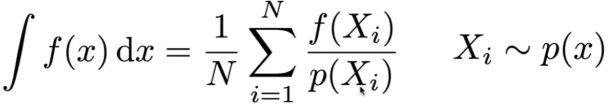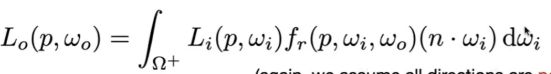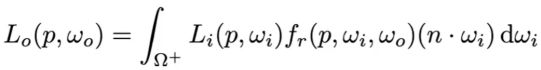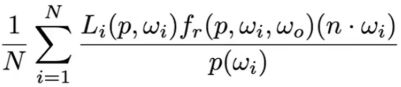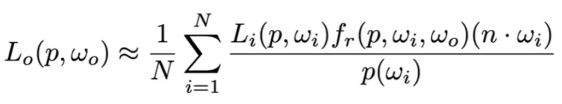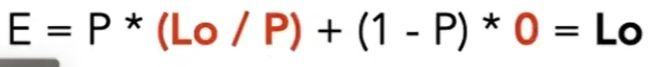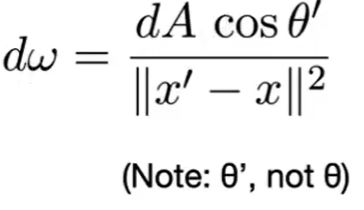Games101-课程16笔记
目录
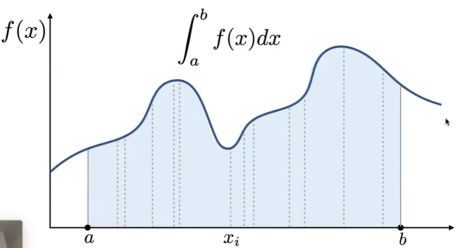
蒙特卡罗积分
(Why)为什么要用蒙特卡罗积分?
(How)怎么使用蒙特卡罗积分?
示例: 均匀蒙特卡罗积分
蒙特卡罗积分公式
路径追踪
对于有光泽的材质,光线应该在哪里反射?
漫反射材质之间没有反射?
简单的蒙特卡罗方法: 用于直接光照
得到直接光照的正确着色算法
算法伪代码
全局光照(加入了间接光照)
目前为止的算法伪代码
一个问题: N(反射光线)过多计算量爆炸
解决方法
解决了N过多问题的路径追踪
但是由于N=1,导致噪声大
解决方法
生成射线伪代码
还有一个问题: 递归不会停止
怎么解决? 引入(RR)俄罗斯轮盘赌
通过加入RR得到的路径追踪
现在我们已经有了正确版本的路径追踪, 但这并不是很有效
了解效率低下的原因
拆分成两部分的radiance(辐射度)的算法
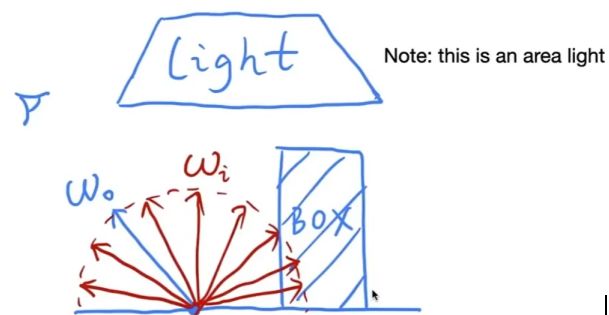
如何知道灯上的样品光线是否没有被阻挡?
最终版本路径追踪
以前的光线追踪vs现代的光线追踪
以前
现代(闫大神对Ray tracing的定义)
具体算法中遇到的问题(有兴趣自行查找答案)
第十六节课: 蒙特卡罗路径追踪( Monte Carlo Path Tracing )
蒙特卡罗积分
(Why)为什么要用蒙特卡罗积分?
我们想求解一个积分,但解析不定积分求解可能太难了
(How)怎么使用蒙特卡罗积分?
通过平均函数值的随机采样来估计函数的积分 (类似黎曼积分 : 通过切割近似成矩形面积的和与“曲线下方”的面积的差需要越来越小, 这样会越来越准确)
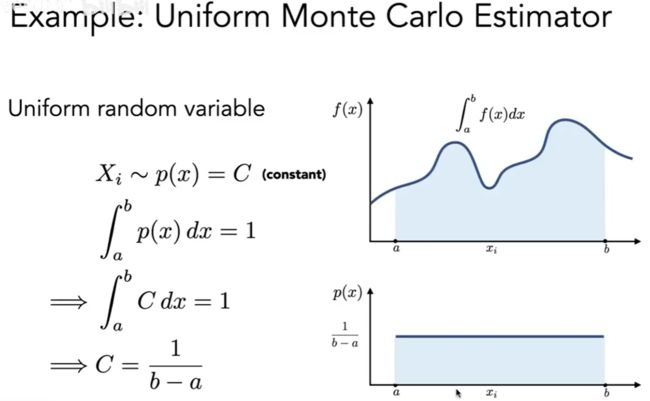
示例: 均匀蒙特卡罗积分
均匀随机变量
让我们为给定函数的定积分定义蒙特卡罗积分
蒙特卡罗积分公式
p(Xi) == 1/b-a
注意事项:
① 样本越多, 方差(误差)越小
② 在 x上采样, 则在 x 上积分
Path Tracing(路径追踪)
whitted 风格的光线追踪-总是执行镜面反射/折射
这些简化合理吗?
更深一层:让我们逐步改进 whitted 风格的光线追踪并引入我们的路径追踪算法!
对于有光泽的材质,光线应该在哪里反射?
光泽茶壶被光线射中, 不能按照光线追踪的计算得到结果, 因为它的表面比镜面材质要粗糙, 应该是在光线射中茶壶某个点时, 它的周围也会被这个点所反射到光照射到.
Mirror reflection: 镜面反射
Glossy reflection: 光泽反射
漫反射材质之间没有反射?
答:
① 两个图都使用Path tracing, 里面的盒子物体是漫反射材质
② 当光线从头顶光源发射到红色墙面时, 反射到带有漫反射材质的长方形面上, 物体某个点接受到反射光后均匀的反射到各个方向(那一面呈现出红色)
③ 人们称这种现象: color-bleed(颜色流出)
总结: 漫反射材质是有反射的. 显然Whitted-Style Ray Tracing不符合, 因为它只会反射和折射.
whitted 风格的光线追踪是错误的
渲染方程是正确的, 它涉及 ① 求解半球上的积分 ② 递归执行
1.如何以数值方式求解积分?
蒙特卡罗方法!
简单的蒙特卡罗方法: 假设我们只想在以下场景中渲染一个像素(点)以用于直接光照
假设只有直接光照(不考虑反射,自发光)
稍微滥用反射方程的概念
再次,我们假设所有方向都指向外面
上面的式子看起来很复杂, 其实就是各个方向的半球积分
所以,当然我们可以使用蒙特卡罗积分来解决它
我们要计算 p 点处朝向相机的辐射度
蒙特卡洛积分:
f(x):
pdf (等于积分式子p(Xk)):
(假设对半球进行均匀采样, 球面面积4Πr , 半球的x轴区间为0~2Π,整个pdf积分为1, 那么p(wi)自然等于1/2Π)
通过上述的假设推理, 代入f(x) 和 p(x) 得到:
这意味着得到直接光照的正确着色算法.
相关参数详解如下:
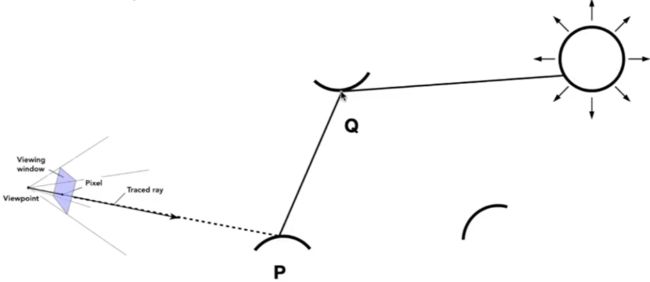
wo: 观测方向 wi: 入射方向 p: 着色点(光照点) n: 法线
算法伪代码如下:
shade(p,wo)
从着色点发出不同方向光线, 选择其中的 N个, 命名wi , 按照某一种pdf
初始化辐射度Lo
对于任何一个入射方向wi
从p(光照点)往wi方向发射一条光线
如果光线碰到光源
return Lo
到此为止, 只解决了直接光照的计算. 剩下间接光照
例如下图: Q也将光反射到P!
将它理解为, 从Q点直接光照到P点.
由此引出间接光, 得到全局光照.
全局光照
比直接光照算法多了一条Else If分支:
如果光碰到一个物体而不是一个光源, 则递归shade(所碰物体的P点, 从Q反射来的方向)
因为一开始假设光线都是着色点向外的方向.
目前为止,算法如下:
这样的算法做完了全局光照吗? NO!
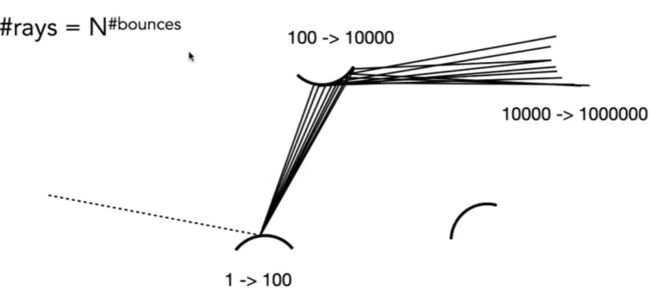
随着#bounces(反弹次数)的增加, #rays(总射线数量)过多, 导致计算量爆炸
#rays(总射线数量) = N(出射射线数量)的#bounces(反弹次数)次方
如果 N= ? ,#rays 不会过多爆炸.
答案是等于1, 如果每次N(出射光线数量)为1.
N大的话, 噪声小;
N小的话, 噪声大, 但是结果是正确的, 噪声越大越不还原.
从现在开始,我们总是假设在每个着色点只追踪 1 条光线:
这就是路径追踪
仅供参考: 当N !=1, 叫做分布式光线追踪, 计算量爆炸.
但这会很吵
没问题,只需通过每个像素追踪更多路径并平均它们的辐射度
生成射线伪代码如下: (非常类似于光线追踪中的光线投射)
ray_generation(摄像机位置, 像素)
在像素里, 均匀地选择 N个样本位置
初始化pixel_radiance(所求值)
遍历在像素里的样本
从摄像机位置往样本位置射向一条射线r
如果射线r碰到场景中物体p
![]()
↑ (平均辐射度操作)
return pixel_radiance
解决了计算量爆炸问题
还有一个问题: 递归不会停止
困境:1.光确实不会停止弹跳
2.切割能量
怎么解决? 引入Russian Roulette(RR)俄罗斯轮盘赌
俄罗斯轮盘赌就是概率
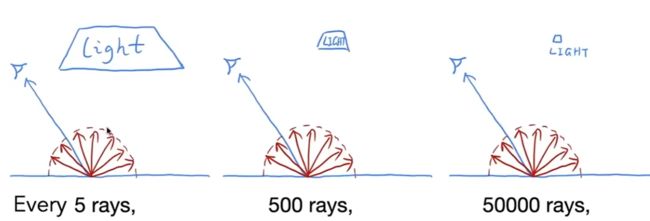
概率为 0 以前,我们总是在一个着色点上射一条射线,得到着色结果 Lo 假设现在我们手动设置一个概率 P(0 ① 以概率 P,射出一条射线并返回(着色结果除以 P):Lo/P ② 以 1-P 的概率,不射光线,你会得到 0 这样,你仍然可以期望得到 Lo: ① 手动设定概率 P_RR ② 在均匀的 dist.in[0,1] 中随机选择 ksi ③ 如果(ksi > P_RR)返回 0.0 ④ 最后只需要: (原有公式) / P_RR SPP(像素里的样本) 左(5根光线就打到光源)中(500根打到光源)右(5w根才打到) 将有 1 条光线击中光源。因此,如果我们在着色点对半球进行均匀采样,则会“浪费”很多光线 这是因为我们之前使用的是半球的均匀采样方法. 所有我们要改变pdf 蒙特卡罗方法允许任何采样方法,因此我们可以对光源进行采样(因此不会“浪费”光线) 假设对光进行均匀采样: pdf = 1/A(因为 ∫pdf dA=1) 但渲染方程整合 立体角上:Lo = ∫Li fr cos dw。 回忆蒙特卡洛积分: 在 x 上采样并在 x 上积分 所以我们在灯光上采样的地方,我们可以在灯光上积分吗? 答案是可以的! ① 需要将渲染方程作为 dA 的积分 ② 需要dw和dA的关系(dw转换为dA) 回忆一下立体角的替代定义:单位球面上的投影面积 然后我们可以将渲染方程重写为 现在在光源上采样! 蒙特卡洛积分: “f(x)”:里面的一切样本 pdf: 1/A 以前,我们假设光线是由均匀半球采样“意外”入摄像机的 现在我们考虑来自两部分的radiance(辐射度): 1.光源(直接,无需RR) 2.其他反射光(间接,RR) ① 注意: 在什么领域采样, 就要在什么领域积分 例如: L_dir(直接光照)使用的是转换后dw->dA在光源采样的渲染方程, 而L_indir(间接光照)使用的是在均匀半球采样且积分的渲染方程 ② 只有间接光照需要RR(俄罗斯轮盘转), 因为是区分直接光照部分.所以那部分不考虑反射, 考虑反射都在间接光照部分. shade(p,wo) 伪代码如下: #来自光源直接光照的贡献 在 x'(pdf_light = 1/A) 处均匀采样光 #来自其他反射光的贡献 初始化总(其它反射光的贡献) L_indir=0.0 用概率 P_RR 测试俄罗斯轮盘赌 将半球均匀地采样到方向 wi (pdf_hemi = 1/2pi) 追踪射线 r (p, wi) 点p往wi方向 如果射线 r 在 q 处击中一个非发射物体 最后一件事: #来自光源的贡献 初始化L_dir = 0.0 在 x'(pdf_light = 1/A) 处均匀采样光 从 p 射出一条射线到 x' 如果光线没有被中间挡住 L_dir=... 被遮挡的都不加进L_dir 现在路径追踪终于完成了 #来自光源的贡献 { 初始化L_dir = 0.0 在 x'(pdf_light = 1/A) 处均匀采样光 从 p 射出一条射线到 x' If光线没有被中间挡住: ps:( 被遮挡的都不加进L_dir } #来自其他反射光的贡献 { 初始化总其它反射光的贡献 用概率 P_RR 测试俄罗斯轮盘赌 将半球均匀地采样到方向 wi (pdf_hemi = 1/2pi) 追踪射线 r (p, wi) 点p往wi方向 If射线 r 在 q 处击中一个非发射物体 } Path Tracing 几乎百分百还原照片既视感 光传输的一般解决方案,包括 ① (单向和双向)路径跟踪 (path tracing) ② 光子映射(photon mapping) ③ metropolis light transport(MLT) ④ VCM/UPBP 1.均匀采样半球 -如何做? 一般来说,问题是如何对任何函数进行采样? 2.蒙特卡罗积分允许任意 pdf 什么是最好的选择?(重要性抽样) 3.随机数重要吗? -是的!(低差异序列) 我们没有涵盖/不会涵盖的东西 我可以采样半球和光源 我可以把它们结合起来吗?是的!(多个 imp.sampling) 像素的辐射度是通过它的所有路径的辐射度平均值 -为什么?(pixel reconstruction filter) 像素的辐射度是像素的颜色吗? - 否(还需要gamma correction, curves, color space) 再问,path tracing还“入门”吗 -这一次,是的,敬畏科学 (闫大神在这节课说: 他什么都不会!!!!!!)通过加入RR得到的路径追踪
现在我们已经有了正确版本的路径追踪, 但这并不是很有效
了解效率低下的原因
拆分成两部分的radiance(辐射度)的算法:
![]()
![]()
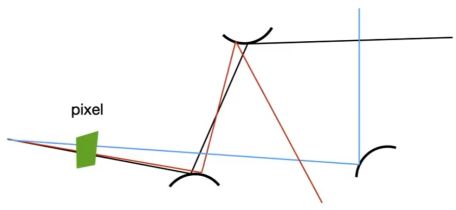
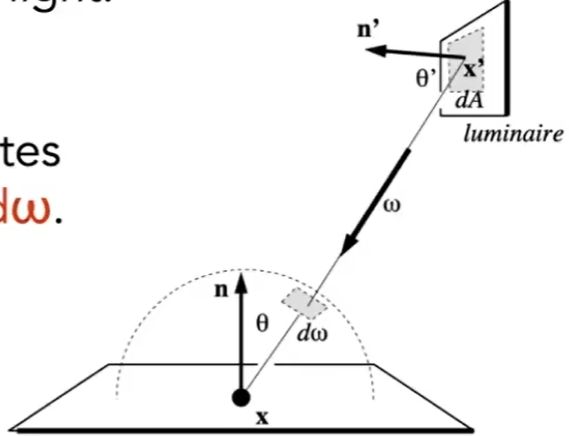
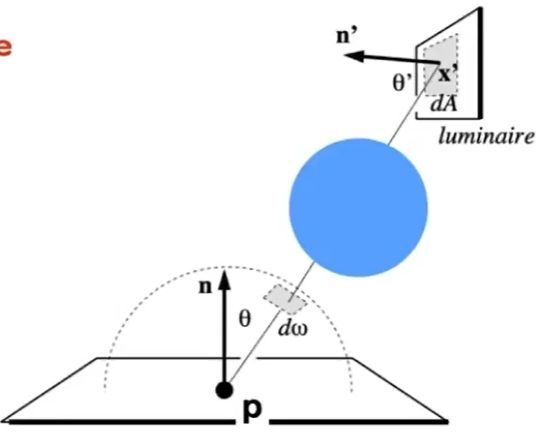
我们如何知道灯上的样品光线是否没有被阻挡?
最终版本路径追踪
![]()
![]() : 入射光与物体法线的夹角;
: 入射光与物体法线的夹角; ![]() : p 射出一条射线到 x'与光源的夹角)
: p 射出一条射线到 x'与光源的夹角)![]()
![]()

以前的:
![]()
现代(闫大神对Ray tracing的定义)
具体算法中遇到的问题(有兴趣自行查找答案)