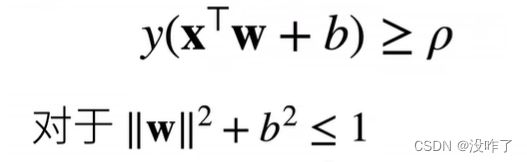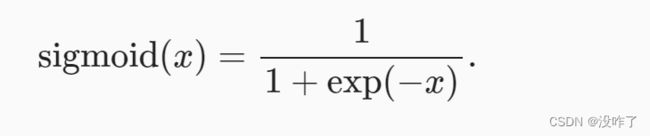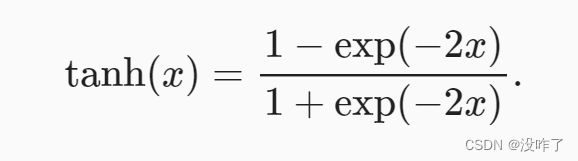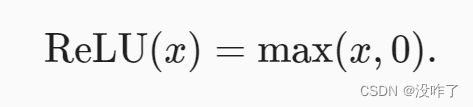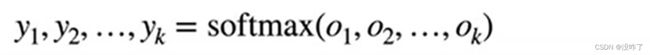感知机&激活函数(动手学深度学习v2)笔记
感知机定义
是二分类模型。给定输入x,权重w,和偏移b,感知机输出: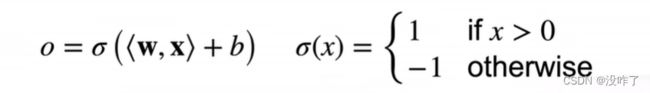
二分类:-1或1(0或1)
Vs.回归输出实数
Vs.Softmax回归输出概率
训练感知机
收敛定理
1、数据在半径 r 内
2、余量 ![]() 分类两类
分类两类
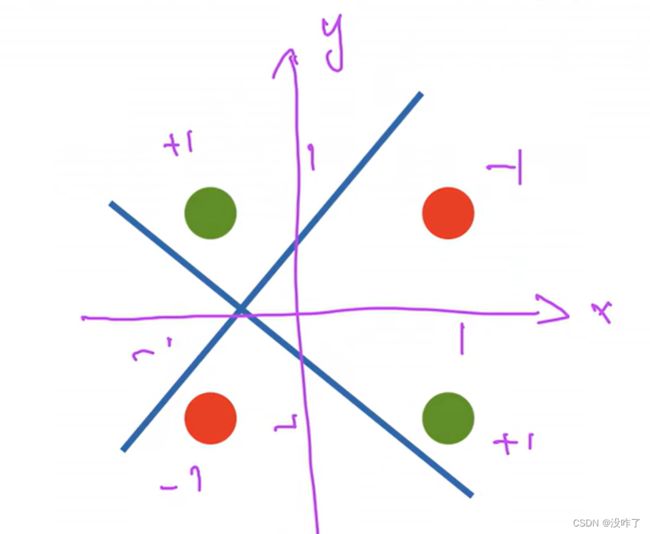
XOR问题(Minsky & Papert,1969)
感知机不能拟合XOR函数,它只能产生线性分割面。
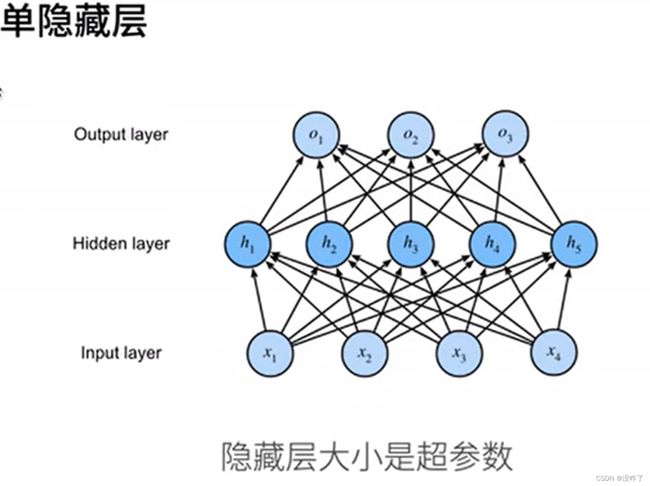
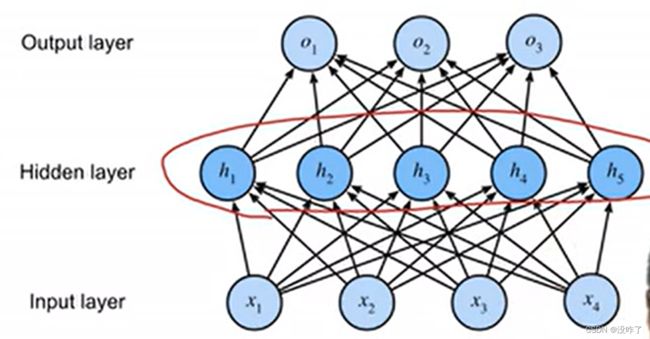
多层感知机
激活函数
激活函数(activation function)通过计算加权和并加上偏置来确定神经元是否应该被激活, 它们将输入信号转换为输出的可微运算。 大多数激活函数都是非线性的。
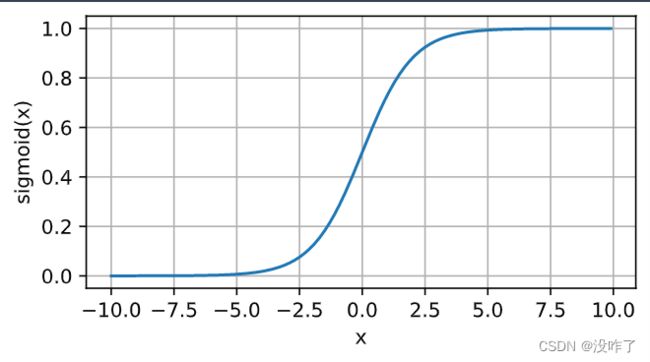
sigmoid函数
定义域在R中的输入,sigmoid函数将输入变换为区间(0, 1)上的输出。 因此,sigmoid通常称为挤压函数(squashing function): 它将范围(-inf, inf)中的任意输入压缩到区间(0, 1)中的某个值。
%matplotlib inline # 将matplotlib的图表直接嵌入到Notebook之中
import torch
from d2l import torch as d2l
x = torch.arange(-10.0, 10.0, 0.1, requires_grad=True)
y = torch.sigmoid(x)
d2l.plot(x.detach(), y.detach(), 'x', 'sigmoid(x)', figsize=(5, 2.5))
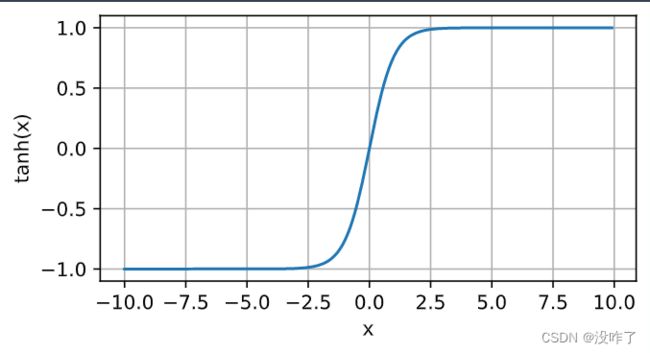
tanh(双曲正切)函数
与sigmoid函数类似, tanh(双曲正切)函数也能将其输入压缩转换到区间(-1, 1)上。
x = torch.arange(-10.0, 10.0, 0.1, requires_grad=True)
y = torch.tanh(x)
d2l.plot(x.detach(), y.detach(), 'x', 'tanh(x)', figsize=(5, 2.5))ReLU函数
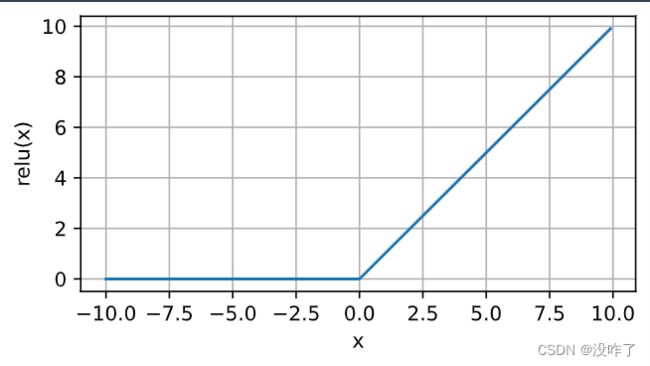
最受欢迎的激活函数是修正线性单元(Rectified linear unit,ReLU), 因为它实现简单,同时在各种预测任务中表现良好。 ReLU提供了一种非常简单的非线性变换。 给定元素x,ReLU函数被定义为该元素与0的最大值:
x = torch.arange(-10.0, 10.0, 0.1, requires_grad=True)
y = torch.relu(x)
d2l.plot(x.detach(), y.detach(), 'x', 'relu(x)', figsize=(5, 2.5))多类分类
总结
- 多层感知机使用隐藏层和激活函数来得到非线性模型
- 常用激活函数是Sigmoid,Tanh,ReLU
- 使用Softmax来处理多类分类
- 超参数为隐藏层数,和各个隐藏层大小
代码从零开始实现:
import torch
from torch import nn
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# 实现一个具有单隐藏层的多层感知机,它包含256个隐藏单元
num_inputs, num_outputs, num_hiddens = 784, 10, 256 # Fashion-MNIST中的每个图像由28*28个灰度像素值组成。所有图像共分为10个类别
W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True) * 0.01) # 784*256
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True)) # 256
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01) # 256*10
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True)) # 10
params = [W1, b1, W2, b2]
# 实现ReLU激活函数,而不是直接调用内置的relu函数
def relu(X):
a = torch.zeros_like(X)
return torch.max(X, a)
# 实现我们的模型
# 因为我们忽略了空间结构,所以我们使用reshape将每个二维图像转换为一个长度为num_inputs的向量
def net(X):
X = X.reshape((-1, num_inputs)) # ?*784
H = relu(X @ W1 + b1) # 这里“@”代表矩阵乘法。[?*784] * [784*256] + [256] = [?*256]
return (H @ W2 + b2) # [?*256] * [256*10] + [10] = [?*10]
loss = nn.CrossEntropyLoss(reduction='none')
num_epochs, lr = 15, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
d2l.predict_ch3(net, test_iter)