【机器学习】吴恩达机器学习个人笔记
文章目录
- 机器学习（Machine Learning）
-
- 监督学习（supervised learning）
- 无监督学习（unsupervised learning）
- 模型表示（Model Representation）
-
- 假设函数（hypothesis function）
- 代价函数（cost function）
- 梯度下降（gradient descent）
- 矩阵与向量（matrices and vector）
- 多特征值（Multiple Features）
-
- 假设函数（hypothesis function）
- 代价函数（cost function）
- 梯度下降（gradient descent）
- 特征缩放（Feature Scaling）
- 学习率α（Learning rate）
- 多项式回归（Polynomial Regression）
- 正规方程(Normal Equation)
- 分类（Classification）
-
- 逻辑回归（Logistic Regression）
-
- 假设表示（Hypothesis Representation）
- 决策边界（Decision Boundary）
- 代价函数（Cost Function）
- 梯度下降（Gradient Descent）
- 进阶优化器（Advanced Optimization）
- 多级分类（Multiclass Classification：One-vs-all）
- 过拟合问题（The Problem of Overfitting）
- 正则化（Regularization）
-
- 正则化线性回归（Regularized Linear Regression）
-
- 代价函数（Cost Function）
- 梯度下降（Gradient Descent）
- 正规方程(Normal Equation)
- 正则化逻辑回归（Regularized Logistic Regression）
- 神经网络（Neural Networks）
-
- 模型表示（Model Representation）
- 应用（Application）
-
- 逻辑运算
- 多分类（Multiclass Classification）
- 代价函数与反向传播（Cost Function and Backpropagation）
-
- 代价函数（Cost Function）
- 反向传播算法（Backpropagation Algorithm）
- 梯度校验（Gradient Checking）
- 随机初始化（Random Initialization）
- 总结
- 评估学习算法（Evaluating a Learning Algorithm）
-
- 评估假设函数（Evaluating a Hypothesis）
- 模型选择（Model Selection）
- 偏差与方差（Bias vs. Variance）
-
- 诊断（Diagnosing Bias vs. Variance）
- 正规化与偏差/方差（Regularization and Bias/Variance）
- 学习曲线（Learning Curves）
- 总结
- 拓展
- 支持向量机（Support Vector Machine）
-
- 优化目标（Optimization Objective）
- 假设函数
- 核函数（kernels）
-
- 高斯核函数（Gauss kernels）
- 支持向量机的参数（SVM parameters）
- 逻辑回归与支持向量机
- 无监督学习（Unsupervised Learning）
-
- K均值算法（K-Means Algorithm）
-
- 优化目标函数（Optimization Objective）
- k-means随机初始化（Random Initialization）
- 选择簇的数量（Choosing the Number of Clusters）
-
- 1.肘部法则（Elbow method）
- 2.根据下游现象（目的或希望得到的结果），手动选择簇的数量【推荐】
- 维数约减（Dimensionality Reduction）
-
- 主成分分析法PCA（Principal Component Analysis）
-
- PCA的步骤
- PCA算法的重建
- PCA中k（降低后的维度）的选择
- 异常检测（Anomaly detection）
-
- 异常检测算法
-
- 异常检测系统的评价
- 异常检测和监督学习的选择
- 异常检测中特征值的选择
- 多元正态分布异常检测
- 推荐算法
-
- 协同过滤算法（Collaborative Filtering）
- 大规模机器学习（Learning With Large Datasets）
-
- 是否要选择大数据量
- 随机梯度下降(Stochastic Gradient Descent)
- 小批量梯度下降(Mini-Batch Gradient Descent)
- 线上学习(Online Learning)
- 映射约减与数据并行(Map Reduce and Data Parallelism)
-
- 映射约减
- 数据并行
- 图像识别(Photo OCR)
-
- 问题描述与流水线(Problem Description and Pipline)
- 滑动窗口(Sliding Windows)
- 获取大量数据喝人造数据(Getting Lots of Data and Artificial Data)
-
- 随机生成数据
- 扩大训练集
- 上限分析(Ceiling Analysis)
机器学习（Machine Learning）
监督学习（supervised learning）
- 有标签的数据作为训练集
- 回归（regression）问题：在连续的输出中预测结果
+ 房价预测，天气预测等 - 分类（classification）问题：对离散的输出结果进行分类
+ 良性与恶性肿瘤的判断等
无监督学习（unsupervised learning）
- 无标签数据作为训练集
- 聚类（clustering）问题：
+ 基因序列归类等 - 非聚类（non-clustering）问题：
+ 鸡尾酒聚会算法
模型表示（Model Representation）
假设函数（hypothesis function）
h θ ( x ) = θ 0 + θ 1 x h_\theta(x)=\theta_0+\theta_1x hθ(x)=θ0+θ1x
代价函数（cost function）
- 目的：使代价函数最小化
- 平方差代价函数（Squared error function）
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_0,\theta_1)={1\over2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2 J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2
梯度下降（gradient descent）
- 通过梯度逐步寻找θ最小值的点，α步长（learning rate）
θ j ≔ θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) ( f o r j = 0 a n d j = 1 ) \theta_j\coloneqq\theta_j-\alpha{\partial\over\partial\theta_j}J(\theta_0,\theta_1) \\(for\ j = 0\ and\ j=1) θj:=θj−α∂θj∂J(θ0,θ1)(for j=0 and j=1) - 所有的θ值需要同时计算，同时更新。（θ0先更新后代入计算θ1是错误的）
- 在线性回归的梯度下降中，只存在一个局部最优解，也就是全局最优解
矩阵与向量（matrices and vector）
- 略
多特征值（Multiple Features）
假设函数（hypothesis function）
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n = θ T x h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n=\theta^Tx hθ(x)=θ0+θ1x1+θ2x2+...+θnxn=θTx
代价函数（cost function）
J ( θ 0 , θ 1 , . . . , θ n ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_0,\theta_1,...,\theta_n)={1\over2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2 J(θ0,θ1,...,θn)=2m1i=1∑m(hθ(x(i))−y(i))2
梯度下降（gradient descent）
θ j ≔ θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 , . . . , θ n ) ( f o r j = 0... n ) \theta_j\coloneqq\theta_j-\alpha{\partial\over\partial\theta_j}J(\theta_0,\theta_1,...,\theta_n) \\(for\ j = 0...n) θj:=θj−α∂θj∂J(θ0,θ1,...,θn)(for j=0...n)
特征缩放（Feature Scaling）
- 目的：优化梯度下降的速度
- 使不同的特征值缩放到近似相同的比例范围（如x1：[0-2000], x2:[0-5]，则令x1 = x1/2000, x2 = x2/5）
- 特征归一化（Mean normalization）
+ 用 xi-μi 代替 xi，使 xi 的平均值接近0
x 1 ← x 1 − μ 1 S 1 x_1\leftarrow{x_1-\mu_1 \over S_1} x1←S1x1−μ1
学习率α（Learning rate）
- 如果α太小：收敛较慢
- 如果α太大：并不会在每次迭代都下降，或者无法收敛
- tip1：如果梯度下降出现异常，可以尝试缩小α值
- tip2：吴恩达个人选择学习率α的经验（仅供参考）
. . . , 0.001 , 0.003 , 0.01 , 0.03 , 0.1 , 0.3 , 1 , . . . ...,0.001,0.003,0.01,0.03,0.1,0.3,1,... ...,0.001,0.003,0.01,0.03,0.1,0.3,1,...
多项式回归（Polynomial Regression）
- 假设函数（hypothesis function）举例
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 = θ 0 + θ 1 ( s i z e ) + θ 2 ( s i z e ) 1 + θ 3 ( s i z e ) 3 x 1 = ( s i z e ) x 2 = ( s i z e ) 2 x 3 = ( s i z e ) 3 \begin{aligned} h_\theta(x)&=\theta_0+\theta_1x_1+\theta_2x_2 \\&=\theta_0+\theta_1(size)+\theta_2(size)^1+\theta_3(size)^3 \\x_1&=(size) \\x_2&=(size)^2 \\x_3&=(size)^3 \end{aligned} hθ(x)x1x2x3=θ0+θ1x1+θ2x2=θ0+θ1(size)+θ2(size)1+θ3(size)3=(size)=(size)2=(size)3
正规方程(Normal Equation)
- 公式计算θ最小值(X前增加一列全为1的特征值)
θ = ( X T X ) − 1 X T y X = [ 1 x 1 ( 1 ) x 1 ( 2 ) … x 1 ( n ) 1 x 2 ( 1 ) x 2 ( 2 ) … x 2 ( n ) ⋮ ⋮ ⋮ ⋮ ⋮ 1 x m ( 1 ) x m ( 2 ) … x m ( n ) ] \theta=(X^TX)^{-1}X^Ty \\ \\ X=\begin{bmatrix} 1 & x^{(1)}_1& x^{(2)}_1&\dots&& x^{(n)}_1 \\1 & x^{(1)}_2& x^{(2)}_2&\dots&& x^{(n)}_2 \\\vdots&\vdots&\vdots&\vdots&&\vdots \\1 & x^{(1)}_m& x^{(2)}_m&\dots&& x^{(n)}_m \end{bmatrix} θ=(XTX)−1XTyX=⎣⎢⎢⎢⎢⎡11⋮1x1(1)x2(1)⋮xm(1)x1(2)x2(2)⋮xm(2)……⋮…x1(n)x2(n)⋮xm(n)⎦⎥⎥⎥⎥⎤
- 优点1：与梯度下降相比，不需要迭代
- 优点2：与梯度下降相比，不需要学习率α
- 优点3：与梯度下降相比，不需要缩放和归一化处理
- 缺点1：需要计算(XTX)-1
- 缺点2：与梯度下降相比，当特征值数量n很大时计算缓慢，而此时梯度下降表现更好
- 缺点3：有些XTX不可逆
- tip1：吴恩达判断n的大小的经验（低于10000选择正规方程，反之选择梯度下降）
- tip2：有时候无法使用正规方程，必须用梯度下降（如分类，聚类等）
分类（Classification）
逻辑回归（Logistic Regression）
假设表示（Hypothesis Representation）
- 期望：0 ≤ hθ(x) ≤ 1
- Sigmoid function:
h θ ( x ) = g ( θ T x ) = 1 1 + e − θ T x g ( z ) = 1 1 + e − z \begin{aligned} h_\theta(x)&=g(\theta^Tx) \\&={1 \over 1+e^{-\theta^Tx}} \\g(z) &= {1 \over 1+e^{-z}} \end{aligned} hθ(x)g(z)=g(θTx)=1+e−θTx1=1+e−z1
- 假设函数的结果为y=1的概率
h θ ( x ) = P ( y = 1 ∣ x ; θ ) = 1 − P ( y = 0 ∣ x ; θ ) P ( y = 0 ∣ x ; θ ) + P ( y = 1 ∣ x ; θ ) = 1 h_\theta(x) = P(y=1 | x ; \theta) = 1 - P(y=0 | x ; \theta) \\ P(y = 0 | x;\theta) + P(y = 1 | x ; \theta) = 1 hθ(x)=P(y=1∣x;θ)=1−P(y=0∣x;θ)P(y=0∣x;θ)+P(y=1∣x;θ)=1
决策边界（Decision Boundary）
- 分割预测y=1与y=0的边界
- 当假设函数大于等于0.5，即z大于等于0，预测y=1
- 当假设函数小于0.5，即z小于0，预测y=0
h θ ( x ) ≥ 0.5 → y = 1 h θ ( x ) < 0.5 → y = 0 θ T x ≥ 0 ⇒ y = 1 θ T x < 0 ⇒ y = 0 \begin{aligned} h_\theta(x) \geq 0.5 \rightarrow y = 1 \\ h_\theta(x) < 0.5 \rightarrow y = 0 \\ \theta^T x \geq 0 \Rightarrow y = 1 \\ \theta^T x < 0 \Rightarrow y = 0 \end{aligned} hθ(x)≥0.5→y=1hθ(x)<0.5→y=0θTx≥0⇒y=1θTx<0⇒y=0
代价函数（Cost Function）
J ( θ ) = 1 m ∑ i = 1 m C o s t ( h θ ( x ( i ) ) , y ( i ) ) C o s t ( h θ ( x ) , y ) = { − log ( h θ ( x ) ) if y = 1 − log ( 1 − h θ ( x ) ) if y = 0 → C o s t ( h θ ( x ) , y ) = − y log ( h θ ( x ) ) − ( 1 − y ) log ( 1 − h θ ( x ) ) \begin{aligned} J(\theta) &= \dfrac{1}{m} \sum_{i=1}^m \mathrm{Cost}(h_\theta(x^{(i)}),y^{(i)}) \\ \mathrm{Cost}(h_\theta(x),y) &=\begin{cases} -\log(h_\theta(x)) \; & \text{if y = 1} \\ -\log(1-h_\theta(x)) \; & \text{if y = 0} \end{cases} \\ \rightarrow\mathrm{Cost}(h_\theta(x),y)&=-y\log(h_\theta(x))-(1-y)\log(1-h_\theta(x)) \end{aligned} J(θ)Cost(hθ(x),y)→Cost(hθ(x),y)=m1i=1∑mCost(hθ(x(i)),y(i))={−log(hθ(x))−log(1−hθ(x))if y = 1if y = 0=−ylog(hθ(x))−(1−y)log(1−hθ(x))
|
|
梯度下降（Gradient Descent）
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] R e p e a t { θ j : = θ j − α m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) } J(\theta) = -\dfrac{1}{m} \sum_{i=1}^m[y^{(i)}\log(h_\theta(x^{(i)}))+(1-y^{(i)})\log(1-h_\theta(x^{(i)}))] \\ \begin{aligned} & Repeat \; \lbrace \\ & \; \theta_j := \theta_j - \frac{\alpha}{m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} \\ & \rbrace \end{aligned} J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]Repeat{θj:=θj−mαi=1∑m(hθ(x(i))−y(i))xj(i)}
进阶优化器（Advanced Optimization）
- “Conjugate gradient”, “BFGS”, and “L-BFGS”
- 优点1：通常比梯度下降快
- 优点2：不需要手动设置学习率α
- 缺点1：比梯度下降复杂很多
- tip：使用函数库直接调用优化器
多级分类（Multiclass Classification：One-vs-all）
- 对每种分类分别执行逻辑回归
y ∈ { 0 , 1... n } h θ ( 0 ) ( x ) = P ( y = 0 ∣ x ; θ ) h θ ( 1 ) ( x ) = P ( y = 1 ∣ x ; θ ) ⋯ h θ ( n ) ( x ) = P ( y = n ∣ x ; θ ) p r e d i c t i o n = max i ( h θ ( i ) ( x ) ) \begin{aligned}& y \in \lbrace0, 1 ... n\rbrace \\& h_\theta^{(0)}(x) = P(y = 0 | x ; \theta) \\& h_\theta^{(1)}(x) = P(y = 1 | x ; \theta) \\& \cdots \\& h_\theta^{(n)}(x) = P(y = n | x ; \theta) \\& \mathrm{prediction} = \max_i( h_\theta ^{(i)}(x) )\\\end{aligned} y∈{0,1...n}hθ(0)(x)=P(y=0∣x;θ)hθ(1)(x)=P(y=1∣x;θ)⋯hθ(n)(x)=P(y=n∣x;θ)prediction=imax(hθ(i)(x))
过拟合问题（The Problem of Overfitting）
- 原因：特征值过多，模型过于复杂
- 解决方法1：减少特征值的数量
+ 手动选择要保留的特征值
+ 使用模型选择算法（model selection algorithm） - 解决方法2：正则化（Regularization）
+ 保留所有特征值，减少θ的大小
正则化（Regularization）
正则化线性回归（Regularized Linear Regression）
- 使θ参数较小
- 对代价函数进行修改，比如我们想要消除多项式中θ3x3的影响，可以在代价函数中加上1000θ32，这会使θ3的代价增高，从而在假设函数中使θ3大幅降低甚至趋于0
代价函数（Cost Function）
- 如下为线性回归的修改后的代价函数：
J ( θ ) = 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 ] J(\theta)={1\over2m}[\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{j=1}^n\theta_j^2] J(θ)=2m1[i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2]
梯度下降（Gradient Descent）
- 梯度下降迭代
Repeat { θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) θ j : = θ j − α [ ( 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ) + λ m θ j ] j ∈ { 1 , 2... n } } \begin{aligned} & \text{Repeat}\ \lbrace \\ & \ \ \ \ \theta_0 := \theta_0 - \alpha\ \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_0^{(i)} \\ & \ \ \ \ \theta_j := \theta_j - \alpha\ \left[ \left( \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} \right) + \frac{\lambda}{m}\theta_j \right] &\ \ \ \ \ \ \ \ \ \ j \in \lbrace 1,2...n\rbrace\\ & \rbrace \end{aligned} Repeat { θ0:=θ0−α m1 i=1∑m(hθ(x(i))−y(i))x0(i) θj:=θj−α [(m1 i=1∑m(hθ(x(i))−y(i))xj(i))+mλθj]} j∈{1,2...n} - θj化简后
θ j : = θ j ( 1 − α λ m ) − α m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j := \theta_j(1-\alpha{\lambda \over m}) - \frac{\alpha}{m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} θj:=θj(1−αmλ)−mαi=1∑m(hθ(x(i))−y(i))xj(i)
正规方程(Normal Equation)
θ = ( X T X + λ ⋅ L ) − 1 X T y where L = [ 0 1 1 ⋱ 1 ] \begin{aligned}& \theta = \left( X^TX + \lambda \cdot L \right)^{-1} X^Ty \\& \text{where}\ \ L = \begin{bmatrix} 0 & & & & \\ & 1 & & & \\ & & 1 & & \\ & & & \ddots & \\ & & & & 1 \\\end{bmatrix}\end{aligned} θ=(XTX+λ⋅L)−1XTywhere L=⎣⎢⎢⎢⎢⎡011⋱1⎦⎥⎥⎥⎥⎤
正则化逻辑回归（Regularized Logistic Regression）
- 代价函数（θ0应使用普通的代价函数）
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta) = -\dfrac{1}{m} \sum_{i=1}^m[y^{(i)}\log(h_\theta(x^{(i)}))+(1-y^{(i)})\log(1-h_\theta(x^{(i)}))]+{\lambda\over 2m}\sum_{j=1}^n\theta_j^2 \\ J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2 - 梯度下降
神经网络（Neural Networks）
模型表示（Model Representation）
- 输入层：输入神经元
- 输出层：输出神经元
- 隐藏层：输入层与输出层中间的激活神经元
- 偏置神经元（bias unit）：对应θ0的隐藏神经元，永远等于1
应用（Application）
逻辑运算
- 神经网络可以用于逻辑运算
- Sigmoid函数中z=4.6时，g(z)=0.99,z=-4.6时，g(z)=0.01
- 比如下例可以得出逻辑或运算的真值表
h Θ ( x ) = g ( − 10 + 20 x 1 + 20 x 2 ) x 1 = 0 a n d x 2 = 0 t h e n g ( − 10 ) ≈ 0 x 1 = 0 a n d x 2 = 1 t h e n g ( 10 ) ≈ 1 x 1 = 1 a n d x 2 = 0 t h e n g ( 10 ) ≈ 1 x 1 = 1 a n d x 2 = 1 t h e n g ( 30 ) ≈ 1 \begin{aligned}& h_\Theta(x) = g(-10 + 20x_1 + 20x_2) \\ \\ & x_1 = 0 \ \ and \ \ x_2 = 0 \ \ then \ \ g(-10) \approx 0 \\ & x_1 = 0 \ \ and \ \ x_2 = 1 \ \ then \ \ g(10) \approx 1 \\ & x_1 = 1 \ \ and \ \ x_2 = 0 \ \ then \ \ g(10) \approx 1 \\ & x_1 = 1 \ \ and \ \ x_2 = 1 \ \ then \ \ g(30) \approx 1\end{aligned} hΘ(x)=g(−10+20x1+20x2)x1=0 and x2=0 then g(−10)≈0x1=0 and x2=1 then g(10)≈1x1=1 and x2=0 then g(10)≈1x1=1 and x2=1 then g(30)≈1
- 同理可以得出与或非等运算以及逻辑运算的复合
多分类（Multiclass Classification）
代价函数与反向传播（Cost Function and Backpropagation）
代价函数（Cost Function）
J ( Θ ) = − 1 m ∑ i = 1 m ∑ k = 1 K [ y k ( i ) log ( ( h Θ ( x ( i ) ) ) k ) + ( 1 − y k ( i ) ) log ( 1 − ( h Θ ( x ( i ) ) ) k ) ] + λ 2 m ∑ l = 1 L − 1 ∑ i = 1 s l ∑ j = 1 s l + 1 ( Θ j , i ( l ) ) 2 J(\Theta) = - \frac{1}{m} \sum_{i=1}^m \sum_{k=1}^K \left[y^{(i)}_k \log ((h_\Theta (x^{(i)}))_k) + (1 - y^{(i)}_k)\log (1 - (h_\Theta(x^{(i)}))_k)\right] + \frac{\lambda}{2m}\sum_{l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}} ( \Theta_{j,i}^{(l)})^2 J(Θ)=−m1i=1∑mk=1∑K[yk(i)log((hΘ(x(i)))k)+(1−yk(i))log(1−(hΘ(x(i)))k)]+2mλl=1∑L−1i=1∑slj=1∑sl+1(Θj,i(l))2
- 符号解释
- L：神经网络中神经元的层数
- sl：第l层神经元的个数
- K：输出神经元的个数/输出的分类数
- 双重求和中使用的代价计算与逻辑回归的代价函数相同
- 与逻辑回归相同，对i=0的项（即偏置神经元）不进行正规化
反向传播算法（Backpropagation Algorithm）
- 目的：使代价函数最小化
- 结果：反向传播算法可以得到J(θ)的偏导数，之后可以使用梯度下降等算法计算出使J(θ)最小的θ值
- 正向传播：从输入层到输出层一层层计算g(θx)得到输出结果
- 反向传播：从输出层开始计算每个神经元的误差，并反向传递给前一层计算前一层的误差（输入层没有误差，因此只计算到输入层的后一层）
- 反向传播算法的过程：
梯度校验（Gradient Checking）
- 校验反向传播算法是否正确
- 通过以下公式计算偏导数的估计值，如果反向传播算法得出的结果与该估计值相似，说明反向传播算法正确
$$
{\partial \over \partial \Theta}J(\Theta) \approx {J(\Theta+\epsilon) - J(\Theta-\epsilon) \over 2\epsilon }
{\partial \over \partial \Theta_j}J(\Theta) \approx {J(\Theta_1,\dots,\theta_j+\epsilon,\dots,\Theta_n) - J(\Theta_1,\dots,\theta_j-\epsilon,\dots,\Theta_n) \over 2\epsilon }
$$
- 为什么不直接用梯度校验代替反向传播算法？
- 梯度校验需要大量的数学计算，速度很慢
随机初始化（Random Initialization）
- 如果Θ初始化为0向量，会导致梯度下降得到的值相同，所以需要随机初始化Θ
总结
评估学习算法（Evaluating a Learning Algorithm）
评估假设函数（Evaluating a Hypothesis）
- 随机拆分数据集为训练集和测试集（70%-30%）
- 测试集的误差函数
-
- 线性回归：
J t e s t ( Θ ) = 1 2 m t e s t ∑ i = 1 m t e s t ( h θ ( x t e s t ( i ) ) − y t e s t ( i ) ) 2 J_{test}(\Theta)={1 \over 2m_{test}}\sum^{mtest}_{i=1}(h_\theta(x^{(i)}_{test})-y^{(i)}_{test})^2 Jtest(Θ)=2mtest1i=1∑mtest(hθ(xtest(i))−ytest(i))2
- 线性回归：
-
- 分类：
e r r ( h Θ ( x ) , y ) = { 1 i f h Θ ( x ) ≥ 0.5 a n d y = 0 o r h Θ < 0.5 a n d y = 1 0 o t h e r w i s e T e s t E r r o r = 1 m t e s t ∑ i = 1 m t e s t e r r ( h θ ( x t e s t ( i ) ) , y t e s t ( i ) ) err(h_{\Theta}(x),y)= \begin{cases}\begin{aligned} &1\ \ if\ h_{\Theta}(x)\geq0.5\ and\ y=0\ or\ h_{\Theta}<0.5\ and\ y=1 \\ &0\qquad\qquad\qquad\qquad otherwise \end{aligned}\end{cases} \\ Test\ Error={1 \over m_{test}}\sum^{mtest}_{i=1}err(h_\theta(x^{(i)}_{test}),y^{(i)}_{test}) err(hΘ(x),y)={1 if hΘ(x)≥0.5 and y=0 or hΘ<0.5 and y=10otherwiseTest Error=mtest1i=1∑mtesterr(hθ(xtest(i)),ytest(i))
- 分类：
模型选择（Model Selection）
- 继续细分数据集为训练集、验证集、测试集（60%-20%-20%）
- 训练集：训练模型
- 验证集：拟合多项式级数，得到一个表现最佳的级数，用于模型选择
- 测试集：评估模型
- 如何拟合多项式级数：
分别对d=1,d=2,...,d=10的多项式进行拟合，并找出表现最好的级数
偏差与方差（Bias vs. Variance）
诊断（Diagnosing Bias vs. Variance）
- 高偏差（欠拟合）时，训练集与验证集的误差函数都很高
- 高方差（过拟合）时，训练集的误差很小，而验证集的误差很大
正规化与偏差/方差（Regularization and Bias/Variance）
- 与多项式级数选择类似，正规化选择的是合适的lamda值
- 分别对λ∈{0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24}的正规化假设函数进行训练，得到合适的λ值
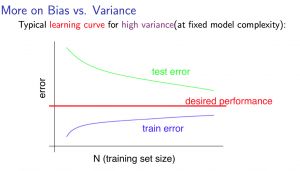
学习曲线（Learning Curves）
-
样本数量与误差的关系
-
训练样本数量极少的时候，往往假设函数可以完美拟合所有样本，而当样本数量不断变大，会有越多的样本无法拟合在假设函数上
-
验证样本与训练样本相反，训练样本数量少的时候，拟合出的曲线对验证样本集的误差更高，而当训练样本数量多的时候，曲线拟合度会更好，验证样本集的误差就越小
-
高偏差（欠拟合）的情况
- 实际上，欠拟合的情况下，训练数据集数量的增加并不会对模型训练起到很大的帮助
- 在学习曲线上表现为：训练集与验证机曲线相差很小
-
高方差（过拟合）的情况
- 更多的训练数据集在高方差的情况下会使模型表现的更好
- 在学习曲线上表现为：训练集与验证机曲线相差很大，随着训练数据量m的增加，两条曲线的距离会快速缩小
总结
- 高方差问题如何解决
- 更多的训练集
- 更少的特征
- 增大正规化lamda值
- 高偏差问题如何解决
- 更少的训练集
- 更多的特征
- 减小正规化lamda值
- 引申到神经网络
- 解决高方差
- 减少隐藏层神经元
- 减少隐藏层层数
- 采用正规化
- 解决高偏差
- 增加隐藏层神经元
- 增加隐藏层层数
- 采用正规化
- 解决高方差
拓展
- 误差分析
- 在搭建模型时，可以考虑先搭建简单模型，再通过学习曲线来对模型进行调整，能有效避免运行前的过度优化
- 手动对模型分类错误的样本进行分析，寻找新的特征值
- 通常使用交叉验证集做误差分析
- 偏斜类（Skewed Classes）
- 正样本的数量与负样本的数量比率接近极端的情况
- 精确率与召回率
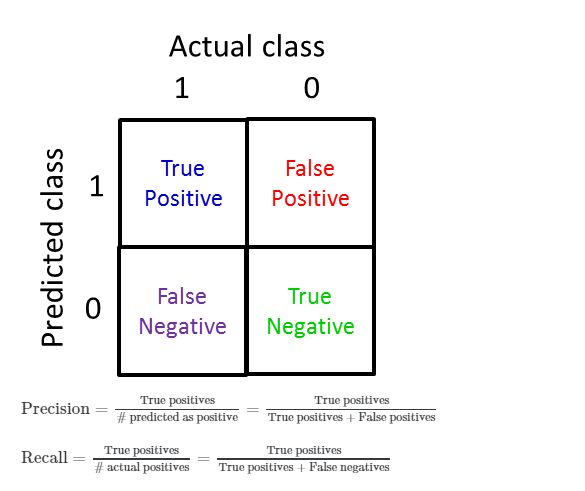
- 通过精确率与召回率判断算法好坏
- P精确率，R召回率
- F1Score:
F 1 S c o r e = 2 P R P + R F_1Score=2{PR\over P+R} F1Score=2P+RPR
支持向量机（Support Vector Machine）
优化目标（Optimization Objective）
m i n θ C [ ∑ i = 1 m y ( i ) cost 1 ( θ T x ( i ) ) + ( 1 − y ( i ) ) cost 0 ( θ T x ( i ) ) ] + 1 2 ∑ j = 1 n θ j 2 \underset{\theta}{min}\ C\left[\sum_{i=1}^{m}y^{(i)}\text{cost}_1(\theta^Tx^{(i)}) + (1-y^{(i)}) \text{cost}_0(\theta^Tx^{(i)})\right]+\frac{1}{2}\sum_{j=1}^n\theta^2_j θmin C[i=1∑my(i)cost1(θTx(i))+(1−y(i))cost0(θTx(i))]+21j=1∑nθj2
假设函数
h Θ ( x ) = { 1 i f Θ T x ≥ 0 0 o t h e r w i s e h_{\Theta}(x)= \begin{cases} \begin{matrix} 1 & if\ \Theta^Tx\geq0 \\ 0 & otherwise \end{matrix} \end{cases} hΘ(x)={10if ΘTx≥0otherwise
核函数（kernels）
θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 ≥ 0 p r e d i c t y = 1 → θ 0 + θ 1 f 1 + θ 2 f 2 + θ 3 f 3 ≥ 0 p r e d i c t y = 1 \theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3\geq0\ \ \ predict\ y=1 \\ \rightarrow\theta_0+\theta_1f_1+\theta_2f_2+\theta_3f_3\geq0\ \ \ predict\ y=1 \\ θ0+θ1x1+θ2x2+θ3x3≥0 predict y=1→θ0+θ1f1+θ2f2+θ3f3≥0 predict y=1
高斯核函数（Gauss kernels）
f i = e − ∣ ∣ x − l ( i ) ∣ ∣ 2 2 σ 2 f_i=e^{-{||x-l^{(i)}||^2\over 2\sigma^2}} fi=e−2σ2∣∣x−l(i)∣∣2
支持向量机的参数（SVM parameters）
- C(=1/λ)
- C太大：低偏差，高方差，过拟合
- C太小：高偏差，低方差，欠拟合
- σ2
- 太大：f函数曲线更平滑，高偏差，低方差
- 太小：f函数曲线不平滑，低偏差，高方差
逻辑回归与支持向量机
- n=特征数，m=训练集样本数
- n很大，m很小，选择逻辑回归或者无核函数的SVM
- n很小且m与n差不多时，选择高斯核函数的SVM
- n很小，m很大时，添加特征值的数量，然后使用逻辑回归或者无核函数的SVM
无监督学习（Unsupervised Learning）
K均值算法（K-Means Algorithm）
- 重复执行两个步骤
- 簇分配（Cluster assignment）：在第一轮中随机设置聚类中心点，将每个数据样本分配给距离最近的聚类中心。在第二轮之后通过移动聚类中心来得到聚类中心，同样将数据样本分配给最近的聚类中心。
- 移动聚类中心（move cluster centroids）：计算每个簇中所有数据样本的均值，并以此得到新的聚类中心
优化目标函数（Optimization Objective）
k-means随机初始化（Random Initialization）
- 要求 K < m
- 随机选择K个训练数据样本作为聚类中心点
- 防止k-means陷入局部最优解，可以多次随机选择聚类中心点，然后从中选择代价函数值最低的解
选择簇的数量（Choosing the Number of Clusters）
1.肘部法则（Elbow method）
- 绘制不同的K值的损失函数图像
- 选择“拐弯”的那个点
- 如果损失函数下降的趋势都很平缓（不好确定“拐弯”点），则肘部法则不适用
2.根据下游现象（目的或希望得到的结果），手动选择簇的数量【推荐】
维数约减（Dimensionality Reduction）
- 将多个特征值压缩成更少的特征值
- 优点：
- 减小存储空间
- 加快计算速度
- 可行性：
- 2维转1维：数据图像近似一条直线，将数据投影至该直线
- 3维转2维：数据图像近似处于一个平面上，将数据投影至该平面
主成分分析法PCA（Principal Component Analysis）
- 目的：对于M维降为K维的案例，需要找到K个向量，将数据样本投影到这些向量组成的维度空间上
- 高维转一维：寻找一个向量，使得维数约减中的数据样本投影到该向量的直线上的距离最小
PCA的步骤
- 特征缩放和均值归一化
- 计算协方差矩阵
Σ = 1 m ∑ i = 1 n ( x ( i ) ) ( x ( i ) ) T \Sigma={1\over m}\sum^n_{i=1}(x^{(i)})(x^{(i)})^T Σ=m1i=1∑n(x(i))(x(i))T - 计算协方差矩阵的特征向量
[U,S,V] = svd(Sigma) - 特征向量矩阵的前k列就是需要的k个向量
Ureduce = U(:,1:k) z = Ureduce'*x
PCA算法的重建
- 将PCA压缩后的数据恢复到原本的维度
X a p p r o x = U r e d u c e ⋅ z ≈ X X_{approx}=U_{reduce}\cdot z\approx X Xapprox=Ureduce⋅z≈X
PCA中k（降低后的维度）的选择
- 选择最小的k值使得
1 m ∑ i = 1 m ∣ ∣ x ( i ) − x a p p r o x ( i ) ∣ ∣ 2 1 m ∑ i = 1 m ∣ ∣ x ( i ) ∣ ∣ 2 ≤ 0.01 ⇔ 1 − ∑ i = 1 k S i i ∑ i = 1 n S i i ≤ 0.01 {{{1\over m}\sum^m_{i=1}||x^{(i)}-x^{(i)}_{approx}||^2} \over {{1\over m}\sum^m_{i=1}||x^{(i)}}||^2} \leq 0.01 \\ \Leftrightarrow 1-{\sum^k_{i=1}S_{ii} \over \sum^n_{i=1}S_{ii}} \leq 0.01 m1∑i=1m∣∣x(i)∣∣2m1∑i=1m∣∣x(i)−xapprox(i)∣∣2≤0.01⇔1−∑i=1nSii∑i=1kSii≤0.01
异常检测（Anomaly detection）
异常检测算法
异常检测系统的评价
- 假设存在10020个带标签的数据样本，其中10000个为0，20个为1
- 可以做以下分配：
- 6000个为0的样本作为训练数据集，做无监督学习训练
- 2000个为0的样本和10个为1的样本作为交叉验证集
- 2000个为0的样本和10个为1的样本作为测试集
- 这样分配可以使用召回率，准确率，F1对模型进行评价
异常检测和监督学习的选择
- 异常检测：
- 正负样本集数量差距非常大
- 异常的种类很多，很难分辨出正样本集中的样本是否是异常样本
- 将来的样本中会出现新的无法预测的异常状况的样本
- 监督学习：
- 正负样本集数量差距不大
- 如果认为将来的样本中将会出现的异常状况会与训练集中出现的异常很相似
异常检测中特征值的选择
- 尽量选择特征图像类似于正态分布的特征值
- 非正态分布的特征值可以使用函数（如取对数，次幂等）转为近似正态分布
多元正态分布异常检测
推荐算法
- 通过给定的标签和用户评分给用户推荐
协同过滤算法（Collaborative Filtering）
- 通过用户的评价和调查来对电影进行种类划分
大规模机器学习（Learning With Large Datasets）
是否要选择大数据量
- 可以画出m与J(θ)的学习曲线，如果表现为高偏差，则不适合用大量数据，如果表现为高方差，则可以使用大量数据进行训练
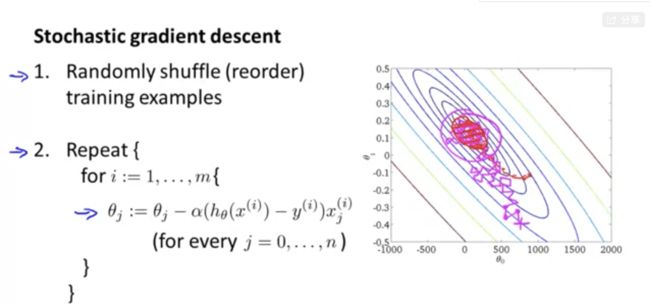
随机梯度下降(Stochastic Gradient Descent)
- 当数据规模较大时，梯度下降每次迭代的计算量会变得很大，因为每次迭代中都要计算所有数据样本的导数求和
- 随机梯度下降的过程
小批量梯度下降(Mini-Batch Gradient Descent)
- 小批量梯度下降与梯度下降和随机梯度下降的对比
- 梯度下降：每轮迭代使用m个数据
- 随机梯度下降：每轮迭代使用1个数据
- 小批量梯度下降：每轮迭代使用b个数据(1
- 小批量梯度下降比随机梯度下降的表现会更好一些
- 相比随机梯度下降，小批量梯度下降的优势在于可以使用向量化来计算每一轮迭代，而不用每个数据单独计算
线上学习(Online Learning)
- 每当一位用户使用你的服务时（此时获取到一组新的数据），使用这组数据对算法进行一次迭代
- 与随机梯度下降相比，线上学习十分相似，每次都是对一组数据进行迭代，不过线上学习是动态获取数据，而随机梯度下降是从静态数据集中每次拿取一组数据
映射约减与数据并行(Map Reduce and Data Parallelism)
映射约减
- 将数据分别派发给数台计算机并行计算，最后汇总到服务器进行迭代
数据并行
- 将数据分别派发给同个计算机中的不同cpu核心进行计算
图像识别(Photo OCR)
问题描述与流水线(Problem Description and Pipline)
- 将问题拆分为不同的部分，可以交由不同的人来完成，最后组成一条流水线
滑动窗口(Sliding Windows)
- 用固定大小的方块，从左到右，从上到下根据步长来扫描图片，并将扫描后的部分传入分类器
- 将得到的结果中分类为1的相邻的部分连接起来，形成一个区域
- 如何将扫描的文字连成一个单词：
- 训练得出所有两个字母之间的空白部分相近的说明为连接在一起的字母
- 最后进行字母识别
获取大量数据喝人造数据(Getting Lots of Data and Artificial Data)
- 在低偏差的算法中，往往庞大的训练集可以起到更好的效果
- 但训练集的获取是有限的，可以通过人造数据来增加训练集的规模
随机生成数据
- 比如在文字识别的系统中，可以通过使用不同的字体库，并对字体图片添加随机的模糊、噪声或者扭曲来生成大量的训练集
扩大训练集
- 在原有样本的基础上进行修改生成新的样本
- 比如在文字识别系统中，对原本的字体图片进行模糊、扭曲、变形等操作，生成大量训练样本。在语音识别系统中，在声音中加入噪声等操作。
上限分析(Ceiling Analysis)
- 计算流水线中每个步骤的准确率，分析每个步骤的优化能对系统整体有多大的提升