一、深度学习与神经网络

前言

我之前的博客写过吴恩达老师的《机器学习》的教程及笔记，之前我一直都喜欢记在本子上，经常本子写满了之后就再去翻阅资料的时候找不到，吴恩达深度学习的视频我之前也看过也做了一些笔记，目前这段时间也比较有空就将一些学习过程的笔记记录下来方便自己以后查阅及学习。本次记录笔记的内容我想换下思路，不再以《机器学习》系列那样做一个课程随笔，我决定还是按照自己的理解，并且以写代码实践为主，将那几课的内容和知识点做一个总结扩充。
代码内容我将以 Keras框架 为基础，至于安装TensorFlow和keras这个自己搞定吧（逃~），所有的代码实现都基于这个框架来实现，当然也有大牛推荐可以自己实现这些算法而不是用一些高级框架，吴恩达视频的前几周也是这个思路。但是我发现实现起来难度很大，特别是深度的反向传播算法，计算每一层的偏导数就非常奔溃，所以还是想以框架为主，只要理解算法即可，就比如我们想开发一个游戏，需要做的是怎么设计这个游戏，而不是连这个游戏引擎也一起写出来（当然也可以，但是代价很大）。
关于Keras也想说一些，Keras是在TensorFlow基础上构建的高层API，比原生API要易用很多。写代码效率很高，关于Keras可以购买 《Python 深度学习》 这本书，写得非常好，非常适合深度学习入门。
另：本系列的所有代码都以jupyter notebook格式托管到github上，大家可以去下载看下
https://github.com/Wangzg123/KerasDeepLearningDemo

一、神经网络及实现

神经网络（neural network） 是机器学习的一种算法，它是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。

1、什么是神经网络算法

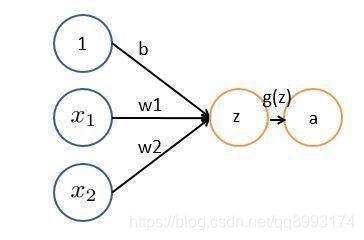
下面我们来看一个直观的例子，比如各大教程最喜欢讲的房价预测的问题，我们有这样的两个变量x₁——表示房子的面积数，x₂——表示房间数目，那么我们怎么预测这个房子的模型？根据这个模型我们有
z = w₁x₁ + w₂x₂ + b
根据由于在房价预测的模型中是一个线性问题（随着x的变化而变化），那么我们激活函数（下面介绍）g(z) = z，则房价
a = g(z) = g(w₁x₁ + w₂x₂ + b) = w₁x₁ + w₂x₂ + b
这就是一个最简单的神经网络算法，通过某个映射关系将x 变为 a，这就是神经网络算法。我们可以把下面的模型向量化来表示
X = [x₁ ，x₂] W = [w₁，w₂]，a = W^TX。

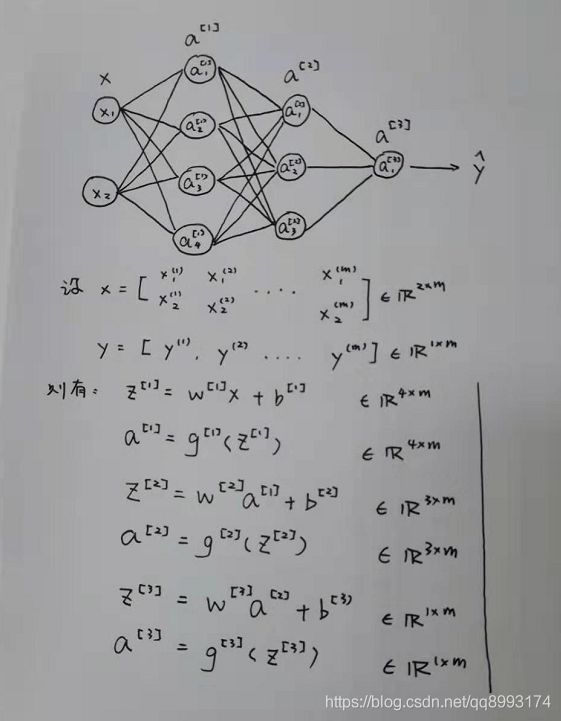
有了上面这个单节点的神经网络的概念，我们来看一个多层神经网络的概念，假设有下面的网络节点，根据上面的公式我们就可以得到下面的计算图，值得注意的是，这里面有个 权重值w和偏移值b 分别是多少乘以多少的矩阵的概念。如
a^[1] = w^[1]X + b^[1]
已知a^[1]有4个节点，X是(2, m)，那么根据矩阵乘法，w^[1] 就是一个(4, 2)的矩阵，b^[1]是一个[4, 1]的矩阵，依次类推根据下面的节点数可以得到权重w和偏移b的shape是
w^[1] = （4, 2）b^[1] = (4, 1)
w^[2] = （3, 4）b^[2] = (3, 1)
w^[3] = （1, 3）b^[3] = (1, 1)
我们可以得到这样的规律，w的形状（当前层的节点数，上一层的节点数）b的形状是（当前层的节点数， 1） 这个概念真的非常非常重要（我在面试别人的时候，很多人不会算，然后接下来的面试我都怀疑他们那些高大上的项目是怎么来的了）而在TensorFlow中几乎每一层都需要我们自己手动算，所以你要很清楚这个概念，并且熟记于心。

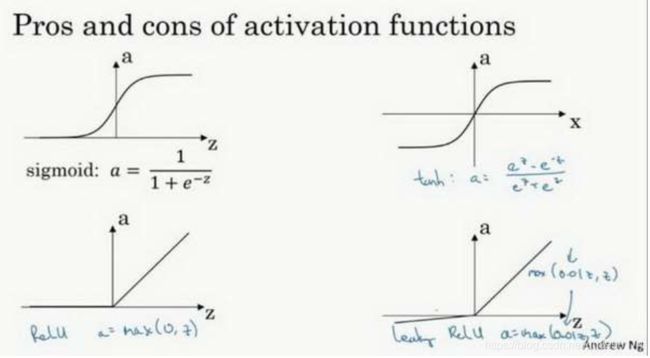
2、激活函数

上面我们看到了g(z）这个激活函数，那么什么是 激活函数（Activation Function） 呢？通俗一点讲就是负责将神经元的输入映射到输出端。下面来看几个常用的激活函数。其中sigmoid常用于二分类问题，relu是由于其导数没有突变性是最常应用的了，而tanh在循环神经网络中经常用到。

那么问题来了，为什么要用激活函数呢？这是因为如果不用激活函数，那么神经网络算法就是一个最简单的线性叠加函数，我们来推导看下面的公式来推导以下就知道了。假如有个两层的网络结构
z^[1] = w^[1]X + b^[1]
z^[2] = w^[2]z^[1] + b^[1] = w^[2] * (w^[1]X + b^[1])+ b^[1] = w^[2] w^[1]X + w^[2]b^[1] + b^[1]
其中w^[2] w^[1] = W ，w^[2]b^[1] + b^[1] = B，那么最后的式子可以看成是z^[2] = WX + B，那么网络的深度根本就没有什么意义，没有激活函数的神经网络算法就是一个简单的线性叠加函数而已。

3、正向、反向传播算法

我们上面看到神经网络输出最后的值，也就是我们的预测值，用来衡量预测值和实际值得偏差的我们称为损失函数，而把所有的样本的损失函数相加起来的平均值就是代价函数，我们预测的目的就是使代价函数最小化，通常是通过梯度下架法来实现的，这里我就不详细讲梯度下降法了，可以查阅我之前的博客或者自己去了解，简单的说梯度下降法就是可以找到代价函数最小值的算法，其中有很多变式，我们下一章节再介绍。
正向传播算法就是根据神经网络模型的一层一层方向去计算代价函数，而反向传播算法就是根据导数的链式法则计算每个权重值偏导数。详细可以查阅我之前的博客 ——《吴恩达机器学习》9 神经网络参数的反向传播算法

4、基于MNIST的算法实现（浅层）

下面我们来看一个例子，就是MNIST手写数据集的实现。这个例子几乎在各大教程及视频中都会说到，详细我就不介绍这个是什么了，这个数据集简直可以称为机器学习领域的hello world，废话不多说，直接上代码，我们来建造一个浅层的神经网络，顺便也介绍一下Keras的实现。

# 导入必要的keras数据
from keras.utils.np_utils import to_categorical
from keras.datasets import mnist
# 导入mnist数据集
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
# 数据预处理
train_data = train_images.reshape((train_images.shape[0], train_images.shape[1]*train_images.shape[2]))
train_data = train_data.astype('float32')/255
test_data = test_images.reshape((test_images.shape[0], test_images.shape[1]*test_images.shape[2]))
test_data = test_data.astype('float32')/255
# 转换为one-hot码
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)
# 划分数据集为训练集和验证集
x_val = train_data[:10000]
x_train = train_data[10000:]
y_val = train_labels[:10000]
y_train = train_labels[10000:]
# 定义一个浅层的网络，第一层是32个节点，第二层是softmax分类层
def shallow_network():
    model = models.Sequential()
    model.add(layers.Dense(32, activation='relu', input_shape=(28*28, )))
    model.add(layers.Dense(10, activation='softmax'))
    model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['acc'])
    return model
# 开始训练
shallow_model = shallow_network()
his_shallow = shallow_model.fit(x_train, y_train, epochs=5, batch_size=128,validation_data=(x_val, y_val))
his_shallow_dict = his_shallow.history
print(his_shallow_dict.keys())
test_shallow_loss, test_shallow_acc = shallow_model.evaluate(test_data, test_labels)
print('shallow_acc ', test_shallow_acc)

结果输出如下：shallow_acc 0.9512，可以看到这样简单的一个神经网络，就可以使得测试集的准确率达到95%

二、深度神经网路

1、什么是深度神经网络算法

有了上面几个简单的浅层神经网络的算法之后，外界一直在提到的深度学习，那么深度体现在哪里，深度主要体现在两个层面上，一个是更深的层数，一个是更多的节点，如下示，这是一个4层神经网络，每层都有好几个节点，这就是深度神经网络。

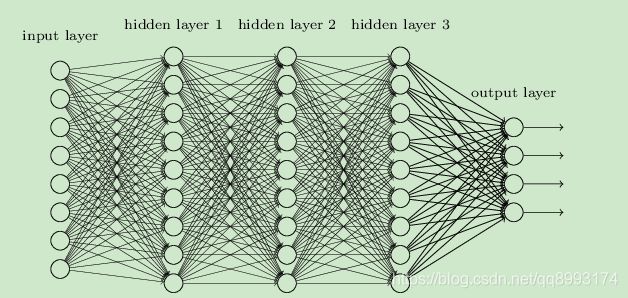
2、基于MNIST的算法实现（深层）

上面我们实现了一个浅层的神经网络（2层网络），下面来实现以下更深层的网络（其实就多了2层。。。）及将这两个网络做下对比

# 以下代码承接上面的代码
# 创建一个更多节点和更多层的网络
def deeper_network():
    model = models.Sequential()
    model.add(layers.Dense(64, activation='relu', input_shape=(28*28, )))
    model.add(layers.Dense(64, activation='relu'))
    model.add(layers.Dense(10, activation='softmax'))
    model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['acc'])
    return model
# 开始训练
deeper_model = deeper_network()
his_deeper = deeper_model.fit(x_train, y_train, epochs=5, batch_size=128,validation_data=(x_val, y_val))
his_deeper_dict = his_deeper.history
print(his_deeper_dict.keys())
test_deeper_loss, test_deeper_acc = deeper_model.evaluate(test_data, test_labels)
print('deeper_acc ', test_deeper_acc)

结果输出如下：deeper_acc 0.9702，可以看到相对于上面的浅层的神经网络，其准确率97%比95%高了两个百分点。我们下面来看下更直观的看下这两个网络的对比吧

import matplotlib.pyplot as plt
shallow_acc_value = his_shallow_dict['acc']
deeper_acc_value = his_deeper_dict['acc']
Epchos = range(1, len(deeper_acc_value) + 1)
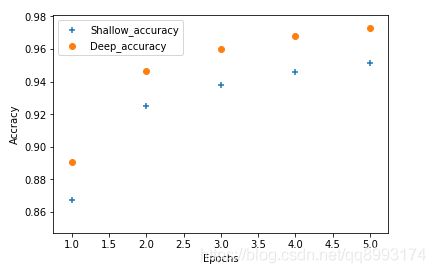
plt.scatter(Epchos, shallow_acc_value, marker='+', label='Shallow_accuracy')
plt.scatter(Epchos, deeper_acc_value, marker='o', label='Deep_accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accracy')
plt.legend()
plt.show()

上面是python的绘制图像的库，下面是输出（我只循环了数据集5次，所以点数有点少，感兴趣可以把epochs设置高一点）看出无论是深层的网络比浅层的表现要好（其实不总是这样的，下篇文章再谈论下这个事情，笑~~~）

三、总结

我们上面介绍了神经网络算法，激活函数，前向传播和反向传播，其中我划分了数据集为训练集和验证集，Keras也没有太详细的介绍，我准备再花点时间整理下Keras的文章（希望有时间。。。），并且举了一个例子来比较浅层网络和深层网络的区别，。但是更加要注意的是并不是越深的网络越好，越深的网络只是意味着能预测更加复杂的模型，但是越深的网络也更容易过拟合，我们调试起来也越麻烦，下一章节准备谈下深度学习的一些方法，包括超参数调优，几个优化器的介绍和解决过拟合的问题，这样会对深度学习构建模型有一个比较清晰的认识。