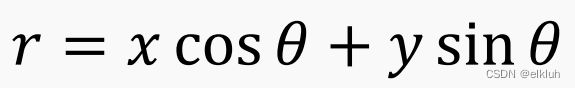霍夫变换讲解

在图像中找形状

Hough transform

检测直线

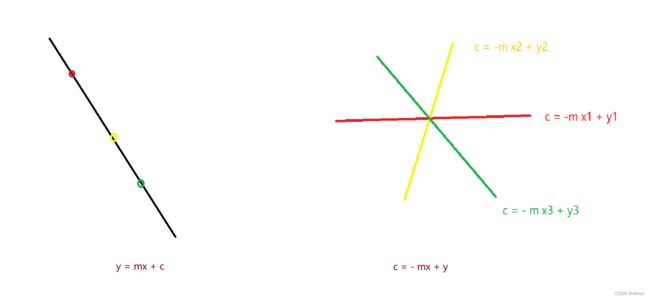
霍夫变换是一种找直线的方法，设一个点为(x, y)，过这个点的直线可以用 y = mx + c 来表示。

那么c = -mx + y。

把(c, m)看作一个点，一条直线是由(c, m)来决定的。如果我们这条线上有很多点，那么我们在画出(c,m)所代表的点时，一定会有很多次。

就是说我们对这条直线上的点，预设一个m值，就可以算出一个c值。如果这些点都在一条直线上，当我们设到真正的m值的时候，这些点都会得到同一个c值。因为这些点的m,c是一样的。

比如左边是y = mx + c ，那么以红点为标准，过这个点的直线为 y1 = m x1 + c, 当我们的m取不同的值的时候，他们的x1，y1都是一样的。所以当我们转换到c，m坐标系。则 c = - x1 m + y1， 也可以表示成一条经经过点(x1 , y1)直线。因为我们要求的直线（左图）是一条过红点的直线，所以它可以是是直线右图红线上面的任意一个点。

同理，当我们换第二个黄点，c = - x2 m + y2 ，也是一条过(x2, y2)的直线， 因为我们要求的直线（左图）是一条过黄点的直线，所以它是右图黄线上面的任意一个点。当我们画了至少两条这样的直线，我们就可以得到交点(c0, m0)。就是我们所要求的左图的的直线的参数。

当m,c趋于无穷时，是一个问题。

所以用上述极坐标也可以表示。

Matlab代码如下所示：

%Hough Transform for Lines
function HTLine(inputimage)
%image size
[rows, columns] = size(inputimage)
%accumulator
acc1 = zeros(rows, 91)
acc2 = zeros(columns, 91)

%image
for x = 1:colimns
    for j = 1:rows
        if(inputimage==0)
            for m=-45:45
                b=round(y-tan(m*pi/180)*x) %因为斜率可以取的值太多了 我们用角度的变换来代替斜率
                if b0
                    acc1(b,m+45+1)= acc1(b,m+45+1)+1; %这个角度下c的值很小
                end
            end
            for m=45:135
                b = round(x-y/tan(m*p/180));
                if b0
                    acc2(b,m-45+1)=acc2(b,m-45+1)+1; %这个角度下c很大，所以换了一种方式 x = (y-c)/m
                end
            end
        end
    end
end

霍夫变换检测圆形

霍夫变换可以用极坐标表示，所以也可以用来检测圆形。

圆的方程为 (x-x0)^2 + (y-y0)^2 = r^2

这个方程可以用两种对偶的方式进行可视化。一种是我们常规的方式，以（x0， y0）为圆心，r为半径做圆。它的对偶形式是，以（x, y）为圆心（也就是圆周上的点），r为半径做圆。

圆的方程可以表示为，x = x0 + r cos(theta), y = y0 + r sin(theta)

则霍夫变换后，x0 = x - r cos(theta), y0 = y - r sin(theta)

这些等式定义了累加空间的点，取决于半径r。

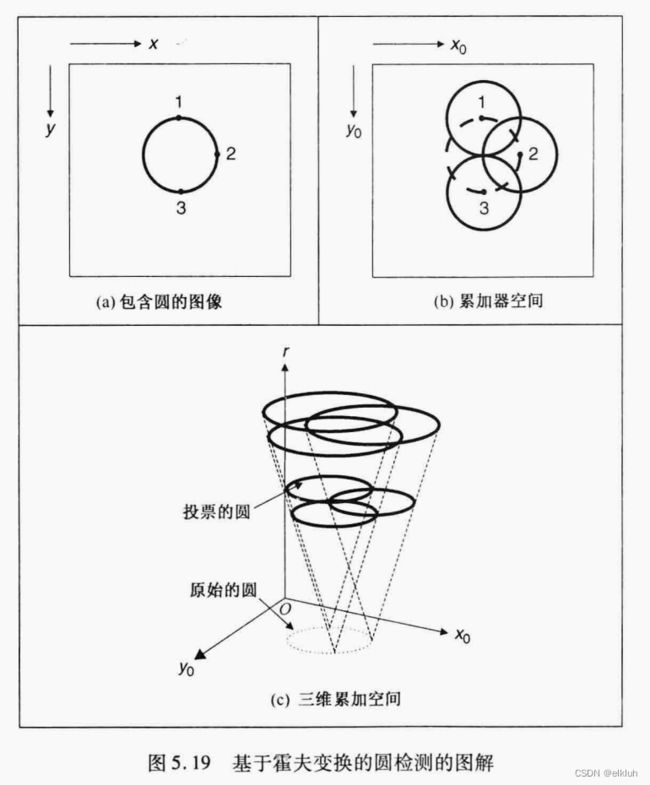
看b图，1,2,3是圆周上的三个点，我们知道了圆心上的三个点，不知道圆心和半径。

设点1， 2， 3分别为（x1, y1）(x2, y2) (x3, y3)

则

x0 = x1 - r cos(theta),    y0 = y1 - r sin(theta)        

x0 = x2 - r cos(theta),y0 = y2 - r sin(theta)

x0 = x3 - r cos(theta),y0 = y3 - r sin(theta)

这里面(x0, y0)是两个未知数，当我们确定r之后，我们可以确定图(b)中的三个圆，如果我们找到的是正确的r，那么这三个圆的交点必定在同一点，也就是说在投给这一点的投票是最多的。Matlab的代码如下所示。

(c)图的意思就是模拟我们的整个算法过程，原始的圆就是我们要找的图形，在那之前我们没确定它是圆嘛，就要拿霍夫变换去套。那么我们找到了这个原始的图形上面的一个点，把这个点当做圆心，我们就给这个点设定一个半径，就可以画出一个新的圆，这个新的圆我们通过画360个点围成的，这些都是我们通过这个原始点产生的投票。然后我们找到第二个图形上面的一个点，还是在这个半径下，画出360个点代表一个圆，。。。依次画完这个图像上面所有点围成的圆。这样总点数就等于我们原来的点数n*360,。如果，我们的这个半径是我们要找的圆的半径的画，这些每个点产生的圆肯定都会经过要找的圆的圆心，查考图b。这样这个圆心一共会出现n次，是不是挺多的，这样我们就找出了圆心了。因为如果我们找的半径不是我们原来的图形的圆心，那肯定不会出现那么多次。

%Hough Transform for Circles
function HTcircle(inputimage, r)

%image size
[rows, columns] = size(inputimage)

%accumulator
acc = zeros(rows,columns)

%image
for x=1:columns
    for y = 1:rows
       if (inputimage(y,x)==0)  %像素值为0 表示这里有线
            for ang=0:360   %把角度范围设为[0, 360]这样可以画完一整个圆周
                t = ang*pi/180;
                x0 = round(x-r*cos(t)) %不能得到整数的要取整
                y0 = round(x-r*sin(t))
                if(x00 & y00)
                    acc(y0,x0) = acc(y0, x0) + 1
                end
            end
        end
     end
end
                   

这种圆形检测算法的优点是，在有噪声和有遮挡的情况下，仍然具有良好的检测性能，缺点是它是一种模板匹配，没有利用图像中可以得到的大量的信息，比如使边缘成为投票的约束条件。

霍夫变换过程

1. 对图像中所有的边缘进行逐一查看。

2.设定一个半径的长度r.

3.对于线上的点，把它当作圆心，以r为半径画出以1°为间隔的圆上的点，如果这些点在圆内，则将这个位置的计数加1.

4.统计完所有边缘上的点，并累加每个位置的记数。

5.改变半径的大小，直到试完所有可能的值，

6.统计计数最大的点为圆心，它所对应的半径为半径。