多项式回归与模型泛化

引言

在实际应用场景中，数据之间是线性关系情况是非常少的，数据之前更多的是非线性关系，当数据之间为非线性关系时，可以通过简单的处理，用线性回归算法来分析非线性数据。
线性与非线性的区别：常用于区别函数y =f (x)对自变量x的依赖关系。线性函数即一次函数，其图像为一条直线。 其它函数则为非线性函数，其图像是除直线以外的图像。

多项式回归

多项式回归原理

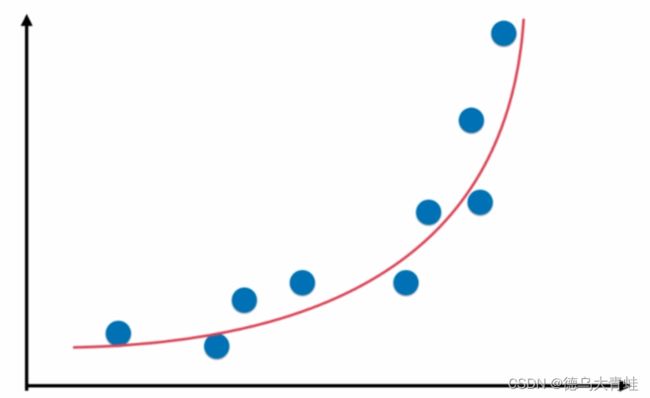
当样本数据分布如下图所示时，如果样本只有一个特征即$x$，样本分布函数为$y=a\ast x^2+b\ast x+c$，此时可以假设样本有2个特征，即样本特征为 $x^2$、$x$，此时可以理解为样本之间为线性关系，但是从原本特征$x$角度看样本是非线性关系。

python实现多项式回归

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

x = np.random.uniform(-3, 3, size=100)
y = 0.5 * x ** 2 + x + 2 + np.random.normal(0, 1, size=100)
X = x.reshape(-1, 1)
x2 = np.hstack([X ** 2, X])

liner_reg = LinearRegression()
liner_reg.fit(x2, y)
y_predict2 = liner_reg.predict(x2)
print(liner_reg.coef_)

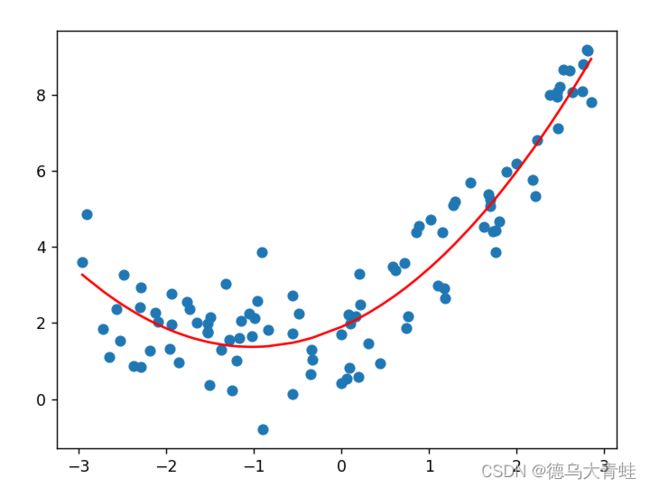
plt.scatter(x, y)
# 由于x是乱的，所以应该进行排序
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()

sklearn实现多项式回归

步骤：
1、PolynomialFeatures将多项式转换
2、LinearRegression对转换后数据训练

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

x = np.random.uniform(-3,3,size=100)
X = x.reshape(-1,1)
y = 0.75*x**2 + x + 3 + np.random.normal(0,1,size=100)

#degree最高次幂
poly = PolynomialFeatures(degree=2)
poly.fit(X)
x2 = poly.transform(X)

lin_reg = LinearRegression()
lin_reg.fit(x2,y)
y_predict = lin_reg.predict(x2)


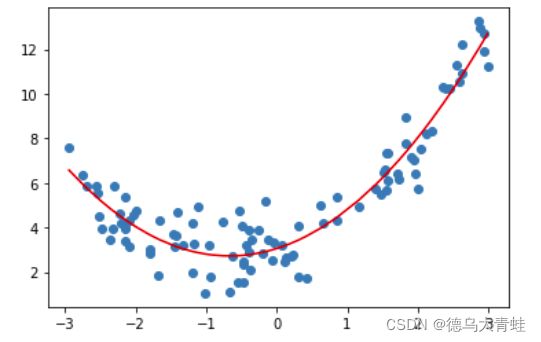
plt.scatter(x,y)
plt.plot(np.sort(x),y_predict[np.argsort(x)],color='r')
plt.show()

其中poly = PolynomialFeatures(degree=2)，ploy生成的新矩阵列为$x^0$到$x^{degree}$方所有排列组合，如存在2个特征，degree=3时，ploy生成的新矩阵列为10

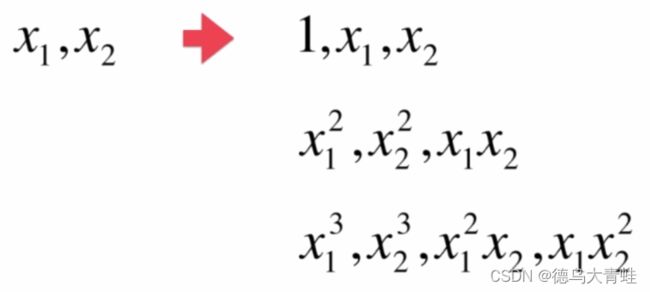
sklearn有个模块Pipeline，使用Pipeline可以将许多算法模型串联起来，比如将特征提取、归一化、分类组织在一起形成一个机器学习问题工作流。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

x = np.random.uniform(-3,3,size=100)
X = x.reshape(-1,1)
y = 0.75*x**2 + x + 3 + np.random.normal(0,1,size=100)


pip = Pipeline([
    ("poly",PolynomialFeatures(degree=2)),
    ("std_scaler",StandardScaler()),
    ("lin_reg",LinearRegression())
])

pip.fit(X,y)
y_predict = pip.predict(X)

plt.scatter(x,y)
plt.plot(np.sort(x),y_predict[np.argsort(x)],color='r')
plt.show()

模型泛化

模型泛化定义

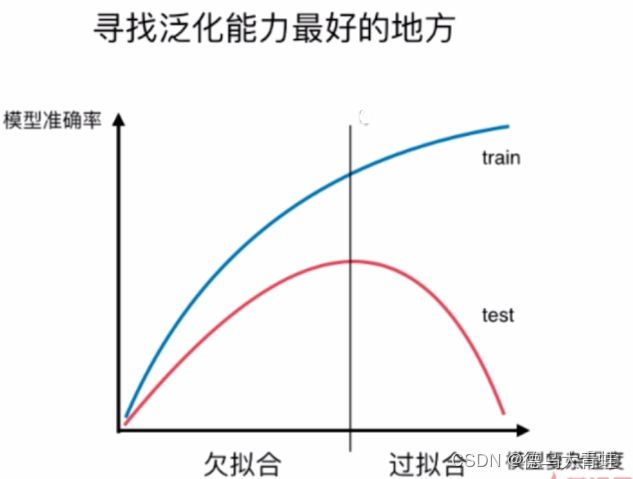
通过训练数据训练出来的模型预测数据的准确率即为模型的泛化能力，当模型预测越准确泛化能力越强。模型预测训练数据越准确，说明模型与训练数据拟合程度越高，这样容易过拟合，泛化能力越弱。

学习曲线

定义

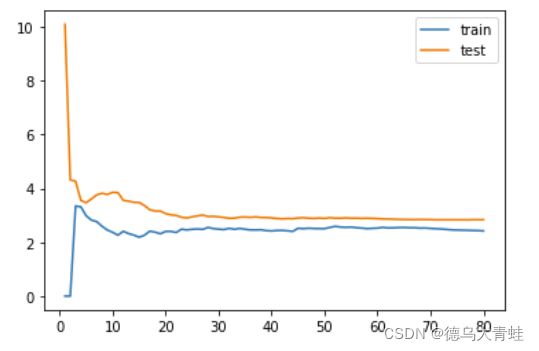
随着训练样本的逐渐增多，算法训练出来的模型的表现能力是如何变化的，变化曲线称为学习曲线。

python实现

线性回归算法

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error

x = np.random.uniform(-3,3,size=100)
X = x.reshape(-1,1)
y = 0.75*x**2 + x + 3 + np.random.normal(0,1,size=100)

x_train,x_test,y_train,y_test = train_test_split(X,y,test_size=0.2)

def plot_learning_curve(algo,x_train,x_test,y_train,y_test):
    train_score = []
    test_score = []

    for i in range(1,len(x_train)+1):
        #随着训练数据增加，预测均方如何差变化
        algo.fit(x_train[:i],y_train[:i])
        y_train_predict = algo.predict(x_train[:i])
        y_test_predict = algo.predict(x_test)
        
        train_score.append(mean_squared_error(y_train_predict,y_train[:i]))
        test_score.append(mean_squared_error(y_test_predict,y_test))
        
        
    plt.plot([i for i in range(1,len(x_train)+1)],np.sqrt(train_score),label='train')
    plt.plot([i for i in range(1,len(x_train)+1)],np.sqrt(test_score),label='test')
    #示例图
    plt.legend()
    #限制x,y轴范围
    #plt.axis([0,len(x_train)+1,0,4])
    plt.show()
 
 plot_learning_curve(LinearRegression(),x_train,x_test,y_train,y_test)       

多项式回归

def PolynomialRegression(degree):
    return Pipeline([
        ("ploy",PolynomialFeatures(degree=degree)),
        ("std_scaler",StandardScaler()),
        ("lin_reg",LinearRegression())
    ])

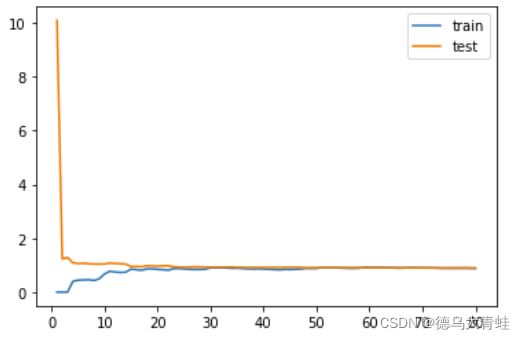
ploy = PolynomialRegression(degree=2)
plot_learning_curve(ploy,x_train,x_test,y_train,y_test)