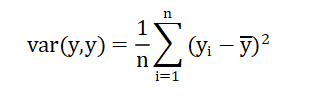协方差计算式及python实现

协方差

最近在学习python的过程中，遇到了计算协方差的问题，借此机会回顾一下协方差的基本知识。

 一些基本定义

样本：https://baike.baidu.com/item/%E6%A0%B7%E6%9C%AC/19974592?fr=aladdin

总体：https://baike.baidu.com/item/%E6%80%BB%E4%BD%93/19951273?fr=aladdin

简言之，样本是抽样得到的结果，总体就是样本的来源

关于协方差的定义

对于样本协方差而言，协方差矩阵cov(X,Y)中的每一项为对于相应两个变量的协方差。

协方差的python实现

由于协方差的计算在实际应用中仅涉及样本协方差的计算，在此仅讨论样本协方差的计算。样本协方差可以用numpy.cov来进行实现

对于两个单独变量的协方差计算：

import numpy as np
x = np.array([1,2,3])
y = np.array([0,3,0])
np.cov(x,y)
# np.cov(x,y)[0][0] #向量x的样本方差
# np.cov(x,y)[0][1] #向量x与y的协方差
# np.cov(x,y)[1][1] #向量y的样本方差

array([[1., 0.],
       [0., 3.]])

计算过程：

对于矩阵之间的协方差计算：

x = np.array([[0, 2], [1, 1], [2, 0]]).T
x

array([[0, 1, 2],
       [2, 1, 0]])

np.cov(x)

array([[ 1., -1.],
       [-1.,  1.]])

ps：可以通过更改参数实现其他功能，例如：

bias : bool, optional
    Default normalization (False) is by ``(N - 1)``, where ``N`` is the
    number of observations given (unbiased estimate). If `bias` is True,
    then normalization is by ``N``. 

即将bias设置为True可以计算有偏的协方差：

 以上若有错误，欢迎指正！