FNN 难以处理时序数据, 比如视频, 语音, 文本等. 时序数据的长度一般是不固定的, 而 FNN 要求输入和输出的维数都是固定的. 因此对这些问题需要能力更强的模型.
如果把 FNN 类比为 Markov chain, 那么 RNN 就是 non-Markovian 的. RNN 的输入与过去一段时间的输出有关, 具有短期记忆. 神经元不但可以接受其他神经元的信息, 也可以接受自身的信息, 形成具有环路的网络结构.
给网络增加记忆能力
延时神经网络 (Time Delay NN)
在 FNN 的非输出层都添加一个延时器, 记录最近几次神经元的输出. 在 \(t\) 时刻, 第 \(l+1\) 层神经元和第 \(l\) 层神经元的最近 \(p\) 次输出相关, 即
\[ h_t^{(l+1)} = f(h_t^{(l)}, \dots, h_{t-p}^{(l)}). \]
由此获得短期记忆的能力.
有外部输入的非线性自回归模型
自回归模型 (autoregressive model, AR) 用一个变量的历史信息来预测自己.
\[ y_t = w_0 + \sum_{i=1}^p w_i y_{t-i} + \varepsilon_t, \]
其中 \(\varepsilon_t\sim N(0, \sigma^2)\) 为时刻 \(t\) 的噪声, 方差与时间无关.
有外部输入的非线性自回归模型 (nonlinear autoregressive with exogenous inputs model, NARX) 是 AR 模型的扩展, 在每个时刻都有一个外部输入 \(x_t\), 产生一个输出 \(y_t\).
\[ y_t = f(x_t,\dots,x_{t-p},y_{t-1},\dots,y_{t-q}). \]
RNN
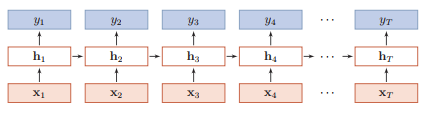
RNN 通过使用带自反馈的神经元, 能够处理任意长度的时序数据.
给定输入序列 \(x_{1:T} = (x_1,\dots,x_T)\), 则 \(h_t = f(h_{t-1},x_t)\), 其中 \(h_0=0\), \(f\) 为激活函数.
简单循环网络 (Simple Recurrent Network, SRN)
SRN 是只有一个 hidden layer 的网络. 相比于 FNN, 增加了隐藏层到隐藏层的反馈连接.
\[ \begin{align*} z_t &= Uh_{t-1} + Wx_t + b,\\ h_t &= f(z_t). \end{align*} \]
参数学习
依然是梯度下降法. 定义 \(t\) 时刻的损失函数为
\[ L_t = L(y_t, g(h_t)), \]
其中 \(g(h_t)\) 为时刻 \(t\) 的输出. 整个序列上的损失函数为
\[ L = \sum_{t=1}^T L_t. \]
RNN 中存在一个递归调用的函数 \(f\), 因此其计算参数梯度的方式和 FNN 不太相同. 主要有两种方式: 随时间反向传播 (backpropagation through time, BPTT) 和实时循环学习 (real-time recurrent learning, RTRL) 算法.
BPTT
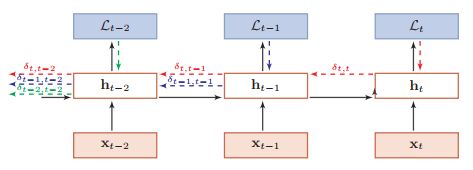
将 RNN 看作是一个展开的多层 FNN, 每一层对应 RNN 的每个时刻, 如前两节的图. 然后按照 FNN 的 BP 算法计算.
误差项
\[ \begin{align*} \delta_{t,k} &= \frac{\partial L_t}{\partial z_k}\\ &= \frac{\partial h_k}{\partial z_k}\frac{\partial z_{k+1}}{\partial h_k}\frac{\partial L_t}{\partial z_{k+1}}\\ &= \mathrm{diag}(f'(z_k))U'\delta_{t,k+1}. \end{align*} \]
导数
\[ \begin{align*} \frac{\partial L_t}{\partial u_{ij}} &= \sum_{k=1}^t \frac{\partial^+ z_k}{\partial u_{ij}}\frac{\partial L_t}{\partial z_k}\\ &= \sum_{k=1}^t\mathbb I_i([h_{k-1}]_j)\delta_{t,k}\\ &= \sum_{k=1}^t [\delta_{t,k}]_i[h_{k-1}]_j, \end{align*} \]
[1] p. 145 写这里要用 '直接' 偏导数 \(\frac{\partial^+ z_k}{\partial u_{ij}}\), 即 \(z_k = Uh_{k-1} + Wx_k + b\) 中保持 \(h_{k-1}\) 不变, 对 \(u_{ij}\) 进行求偏导. (但我没懂为什么可以这样做.) 由此,
\[ \frac{\partial L_t}{\partial U} = \sum_{k=1}^t\delta_{t,k}h_{k-1}'. \]
可得参数梯度
\[ \begin{align*} \frac{\partial L}{\partial U} &= \sum_{t=1}^T \sum_{k=1}^t\delta_{t,k}h_{k-1}',\\ \frac{\partial L}{\partial W} &= \sum_{t=1}^T \sum_{k=1}^t\delta_{t,k}x_k',\\ \frac{\partial L}{\partial b} &= \sum_{t=1}^T \sum_{k=1}^t\delta_{t,k}. \end{align*} \]
RTRL
通过向前传播的方式计算梯度.
\[ \begin{align*} \frac{\partial h_{t+1}}{\partial u_{ij}} &= \left(\frac{\partial^+ z_{t+1}}{\partial u_{ij}} + \frac{\partial h_t}{\partial u_{ij}}U'\right)\frac{\partial h_{t+1}}{\partial z_{t+1}}. \end{align*} \]
两种算法的比较. 一般网络输出纬度远低于输入纬度, 因此 BPTT 算法的计算量会更小, 但是由于需要保存所有时刻的中间梯度, 空间复杂度高. RTRL 不需要梯度回传, 因此非常适合需要在线学习或无限序列的任务中.
长程依赖问题
RNN 学习过程中的主要问题是梯度消失或爆炸问题, 很难建模长时间间隔 (long range) 的状态之间的依赖关系.
把 BPTT 算法中的误差递推公式展开, 得
\[ \delta_{t,k} = \prod_{\tau = k}^{t-1} \left( \mathrm{diag}(f'(z_\tau))U' \right)\delta_{t,t}. \]
若定义 \(\gamma \simeq \Vert \mathrm{diag}(f'(z_\tau))U'\Vert\), 则
\[ \delta_{t,k} \simeq \gamma^{t-k}\delta_{t,t}. \]
当 \(t-k\to\infty\) 时, 若 \(\gamma > 1\), 则 \(\gamma^{t-k}\to\infty\), 称为梯度爆炸问题 (gradient exploding problem). 若 \(\gamma < 1\), 则有梯度消失问题.
Remark: 需要注意的是, RNN 中的梯度消失不是指 \(\frac{\partial L_t}{\partial U}\) 消失, 而是 \(\frac{\partial L_t}{\partial h_k}\) 消失, 这意味着 \(U\) 的更新主要靠当前时刻 \(t\) 的几个相邻状态 \(h_k\) 来更新, 长距离的状态对 \(U\) 没有影响.
虽然 RNN 理论上可以建立长时间间隔的状态之间的依赖关系, 但是由于梯度爆炸或消失问题, 实际上只能学习到短期的依赖关系, 这称为长程依赖问题 (long-term dependencies problem).
改进方案
梯度爆炸一般通过权重衰减 (weight decay) 或梯度截断来避免. 权重衰减是通过正则化来限制参数的取值范围, 从而使得 \(\gamma\le 1\). 梯度截断是一种启发式方法, 当梯度的模大于一定阈值时, 将其截断.
梯度消失的一个有效缓解方式是让 \(U = I\), 同时令 \(\frac{\partial h_t}{\partial h_{t-1}} = I\), 即
\[ h_t = h_{t-1} + g(x_t;\theta). \]
但是这种改变丢失了神经元在反馈边上的非线性激活的性质, 因此也降低了模型的表示能力. 为此, 可以采用一种改进策略
\[ h_t = h_{t-1} + g(x_t, h_{t-1};\theta). \]
但这依然有梯度爆炸问题, 另外还有记忆容量 (memory capacity) 问题. 随着 \(h_t\) 不断积累存储新的输入信息, 会发生饱和现象. 假设 \(g\) 为 Logistic 函数, 则随着时间 \(t\) 的增长, \(h_t\) 会变得越来越大, 从而导致 \(h\) 变得饱和. 也就是说, 隐状态 \(h_t\) 可以存储的信息是有限的, 随着记忆单元存储的内容越来越多, 其丢失的信息也越来越多.
为了解决这两个问题, 可以通过引入门控机制来进一步改进模型.
基于门控的 (Gated) RNN
引入门控机制来控制信息的累计速度, 包括有选择地加入新的信息, 并有选择地遗忘之前积累的信息.
长短期记忆 (long short-term memory, LSTM) 网络
LSTM 可以有效解决梯度爆炸或消失问题. 改进在以下两个方面:
新的内部状态. 引入新的内部状态 \(c_t\) 专门进行线性的循环信息传递, 同时输出信息给隐藏层.
\[ \begin{align*} c_t &= f_t \circ c_{t-1} + i_t \circ \tilde c_t,\\ h_t &= o_t \circ \tanh(c_t), \end{align*} \]
其中 \(f_t\) (遗忘), \(i_t\) (输入), \(o_t\) (输出) 为三个门来控制信息传递的路径, \(\tilde c_t\) 是通过非线性函数得到的候选状态,
\[ \tilde c_t = \tanh(W_c x_t + U_c h_{t-1} + b_c). \]
在每个时刻, \(c_t\) 记录了到当前时刻为止的历史信息.
门控机制.
- 遗忘门控制上一时刻内部状态 \(c_{t-1}\) 需要遗忘多少信息.
- 输出门控制当前时刻的候选状态 \(\tilde c_t\) 有多少信息需要保存.
- 输出门控制当前时刻的内部状态 \(c_t\) 有多少信息需要输出给外部状态 \(h_t\).
门的计算方式为
\[ \begin{align*} ?_t = \sigma(W_? x_t + U_? h_{t-1} + b_?), \end{align*} \]
其中 \(? = i, f, o\).
记忆. \(h\) 存储了历史信息, 可以看作是一种记忆. 在简单 RNN 中, 隐状态每个时刻都会被重写, 因此可以看做是一种短期记忆. 在 NN 中, 长期记忆可以看作是网络参数, 隐含了从训练数据中学到的经验, 其更新周期要渊源慢于短期记忆. 在 LSTM 网络中, 记忆单元 \(c\) 可以在某个时刻捕捉到某个关键信息, 并有能力将此关键信息保存一定的时间间隔. 记忆单元 \(c\) 中保存信息的生命周期要长于短期记忆 \(h\), 但又远远短于长期记忆, 因此称为长的短期记忆 (LSTM).
Remark: 一般深度网络参数初始化的值都比较小. 但在训练 LSTM 网络时, 过小的值会使得遗忘门的值比较小, 丢失大部分前一时刻的信息, 并且会造成梯度消失问题. 因此遗忘的参数初始值一般都设得比较大.
门控循环单元 (Gated Recurrent Unit, GRU) 网络
是一种比 LSTM 网络更加简单的 RNN. GRU 不引入额外的记忆单元, 而是引入一个更新门 \(z_t\),
\[ h_t = z_t\circ h_{t-1} + (1-z_t)\circ g(x_t,h_{t-1};\theta). \]
在 LSTM 网络中, 输入门和遗忘门是互补关系, 有一定冗余. GRU 网络直接使用一个门来控制输入和遗忘之间的平衡.
\[ \tilde h_t = \tanh(W_h x_t + U_h(r_t\circ h_{t-1}) + b_h), \]
其中 \(\tilde h_t\) 表示当前时刻的候选状态, \(r_t\) 为重置 (reset) 门, 用来控制候选状态的计算是否依赖上一时刻的状态.
综上, GRU 网络的状态更新方式为
\[ h_t = z_t \circ h_{t-1} + (1-z_t) \circ \tilde h_t. \]
References
[1] 邱锡鹏. (2019). 神经网络与深度学习. https://nndl.github.io/