LSTM神经网络

       LSTM被广泛用于许多序列任务（包括天然气负荷预测，股票市场预测，语言建模，机器翻译），并且比其他序列模型（例如RNN）表现更好，尤其是在有大量数据的情况下。 LSTM经过精心设计，可以避免RNN的梯度消失问题。消失梯度的主要实际限制是模型无法学习长期的依赖关系。但是，通过避免消失的梯度问题，与常规RNN相比，LSTM可以存储更多的记忆（数百个时间步长）。与仅维护单个隐藏状态的RNN相比，LSTM具有更多参数，可以更好地控制在特定时间步长保存哪些记忆以及丢弃哪些记忆。例如，在每个训练步骤中都必须更新隐藏状态，因此RNN无法确定要保存的记忆和要丢弃的记忆。

     

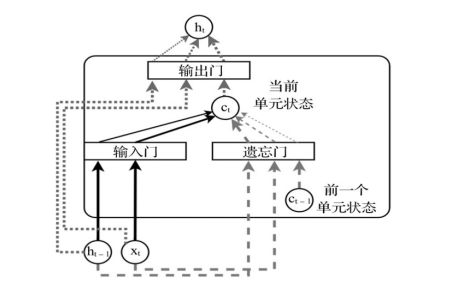
LSTM可以看作是一个更高级的RNN系列，主要由五个不同部分组成。

●单元状态：这是LSTM单元的内部单元状态（例如，记忆）。

●隐藏状态：这是用于计算预测结果的外部隐藏状态

●输入门：确定发送到单元状态的当前输入量

●忘记门：确定发送到当前单元状态的先前单元状态的数量

●输出门：确定隐藏状态下输出的单元状态数

可以将RNN加载到单元架构中，如下所示。该单元输出的状态取决于前一个单元的状态和当前输入（使用非线性激活函数）。但是，在RNN中，单元状态始终随每个输入而变化。这将不断更改RNN的单元状态。此行为对于保留长期依赖关系非常不利。 LSTM可以决定何时以单位状态替换，更新或忘记存储在每个神经元中的信息。这意味着LSTM具有防止单元状态改变的机制，从而保留了长期依赖关系。

采用引入门控机制来实现这种效果。对于单元需要执行的每个操作，LSTM都有一个相应的门。门在0和1之间连续（通常是S型函数）。 0表示没有信息通过门，1表示所有信息都通过门。 LSTM对单元中的每个神经元使用一个这样的门。如前所述，这些门控制以下内容：

●当前有多少输入被写入单元状态（输入门）

●先前单元状态（忘记门）遗忘的信息量

●从单元状态到最终隐藏状态（输出门）的信息输出量

 

      每个门确定发送到状态变量（即，最终的隐藏状态或单元状态）的各种数据（例如，当前输入，先前的隐藏状态或先前的单元状态）的数量。每条线的粗细代表进出闸门的信息量。例如，在此图中，输入门允许从当前输入中获取更多信息，而不是先前的最终隐藏状态（从输入门进入入状态单元），而遗忘门可以可以从先前最终隐藏状态获得更多信息。而不是当前输入，通过遗忘门进入当前单元状态：

                                    

LSTM主要由以下三个门组成。

●输入门：此门输出介于0（输入未写入单元状态）到1（输入已完全写入单元状态）之间的值。Sigmoid激活用于将输出压缩为0到1之间。

●遗忘门：这是一个S型门，其中0（在计算当前单元状态时完全忘记先前的单元状态）和1（在计算当前单元状态时完全忘记先前的单元状态）。

●输出门：这是一个Sigmoid门，输出0（计算最终状态将完全破坏当前的单元状态）和1（计算最终隐藏状态将完全使用当前单元状态）。

 

                                   

       这是一个非常概括的图，其中隐藏了一些细节以避免混淆。为清楚起见，同时显示了LSTM和回路连接。右图显示了具有循环连接的LSTM，左图显示了展开循环连接后的相同LSTM，因此模型中没有环形连接。

 

输入门接收当前输入和最后的最终隐藏状态作为输入，并根据以下公式进行计算：

       

计算后，值为0表示当前输入的任何信息都不会进入单位状态，值为1意味着当前输入的所有信息都将进入单位状态。然后，以下公式将计算另一个值，称为候选值。 它用于计算当前单元状态。

遗忘门将执行以下操作： 遗忘门值为0表示没有的任何信息传递给的计算，值为1意味着所有的信息都传播给

接下来看一下当前状态的计算公式也就是说，当前状态是以下各项的组合：

●要记住/记住的先前单元状态的信息；

●添加/舍弃当前输入信息。

LSTM单元的最后状态计算:

最终隐藏状态的输出与前一个序列的隐藏状态、当前的输入和当前单元状态值有关，用一个tanh激活函数将当前单元状态的值压缩到-1到1之间。先前隐藏状态与当前输入的值通过sigmoid函数转换后与当前单元状态通过压缩后的值进行相乘，就会把先前的状态信息与此时的输入信息进行保留或舍弃得到一个新的隐藏状态值。

                          

在这里，从更大的角度来看，我们展示了如何针对序列学习问题，随着时间的推移扩展LSTM单位，以接收该单元的前一个状态并计算下一个状态。但是，这还不足以做任何有用的事情。即使实际上可以创建一个可以对序列进行建模的LSTM链，也没有输出或预测。但是，如果希望LSTM实际使用学习到的信息，则需要一种从LSTM提取最终输出的方法。 因此，在LSTM的顶部添加一个softmax层（权重Ws和偏置bs）。 最终输出结构如图5-14所示：

 

接下来，来看看LSTM和标准RNN之间的区别。与标准RNN相比，LSTM的结构更为复杂。主要区别之一是LSTM具有两个不同的状态，一个单元状态ct和一个最终的隐藏状态ht。但是，RNN中只有一个隐藏状态。另一个很大的不同是LSTM具有三个不同的门，这使LSTM在计算最终隐藏状态时可以更好地控制其如何处理当前输入和先前的单元状态。

具有两个不同的状态是非常有利的。这种机制使最终的隐藏状态变化相对较慢，即使单元格的状态变化很快。因此，单元状态学习短期和长期依赖性，但最终的隐藏状态仅反映短期依赖性和/或长期依赖性。