CenterNet：Objects as Points
简介
看了一位博主解读CenterNet的博客（https://blog.csdn.net/baobei0112/article/details/94392343），感觉写的不错，转载一下。 内容属于转载！
论文地址：https://arxiv.org/pdf/1904.07850.pdf
发布时间：2019.4.16
机构：UT Austin，UC Berkeley
代码：https://github.com/xingyizhou/CenterNet
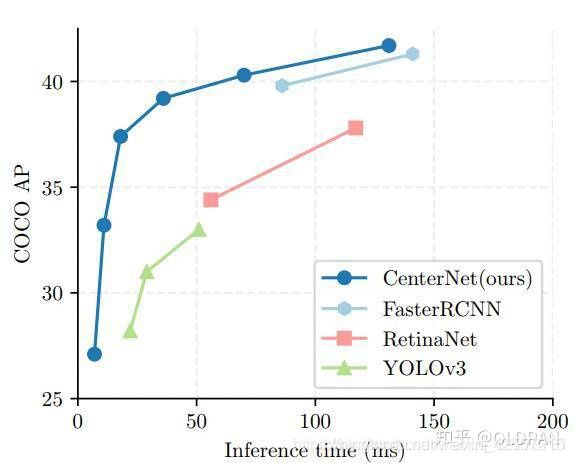
有两个不同CenterNet目标检测算法但是有相同的名称，一个是CenterNet：Objects as Points，另一个是CenterNet：Keypoint Triplets for Object Detection，都是2019年的比较新的目标检测算法，在这里总结的是第一种Objects as Points。第二种CenterNet是完全基于CornerNet改变而来的，相比于CornerNet做出了改进，使得检测速度和精度相比于one-stage和two-stage的框架都有不小的提高，尤其是与YOLOv3作比较，在相同速度的条件下，CenterNet的精度比YOLOv3提高了4个左右的点。
CenterNet不仅可以用于目标检测，还可以用于其他的一些任务，如姿态估计或者3D目标检测等等，但是这篇文章重点说的是其对目标检测的部分，模型实现了速度和精确度的最好权衡。以下是其性能：
MS COCO dataset, with 28:1% AP at 142 FPS, 37:4% AP at 52 FPS, and 45:1% AP with multi-scale testing at 1.4 FPS
网络结构
论文中CenterNet提到了三种用于目标检测的网络，这三种网络都是编码解码(encoder-decoder)的结构：
- Resnet-18 with up-convolutional layers : 28.1% coco and 142 FPS
- DLA-34 : 37.4% COCOAP and 52 FPS
- Hourglass-104 : 45.1% COCOAP and 1.4 FPS
每个网络内部的结构不同，但是在模型的最后都是加了三个网络构造分别来输出80个类（文中用的数据集为80类）的置信度、长宽的预测值以及中心点坐标的偏置值
用官方的源码(使用Pytorch)来表示一下最后三层，其中hm为heatmap、wh为对应中心点的width和height、reg为偏置量，这些值在后文中会有讲述。
(hm): Sequential(
(0): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace)
(2): Conv2d(64, 80, kernel_size=(1, 1), stride=(1, 1))
)
(wh): Sequential(
(0): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace)
(2): Conv2d(64, 2, kernel_size=(1, 1), stride=(1, 1))
)
(reg): Sequential(
(0): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace)
(2): Conv2d(64, 2, kernel_size=(1, 1), stride=(1, 1))
)前提条件
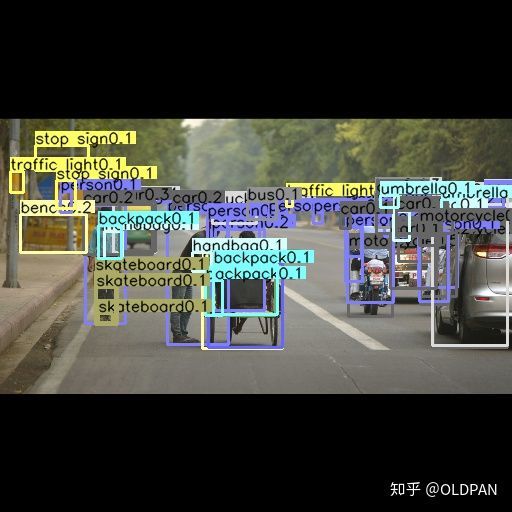
附一张检测的效果图：
我们该如何检测呢？
这样，
就是一个检测到物体的预测值，对于 ，表示对于类别 c，在当前(x,y)坐标中检测到了这种类别的物体，而 
则表示当前当前这个坐标点不存在类别为 c的物体。
在整个训练的流程中，CenterNet学习了CornerNet的方法。对于每个标签图(ground truth)中的某一 C类，我们要将真实关键点(true keypoint) 
计算出来用于训练，中心点的计算方式为 
，对于下采样后的坐标，我们设为
，其中 R是上文中提到的下采样因子4。所以我们最终计算出来的中心点是对应低分辨率的中心点。
然后我们利用 
来对图像进行标记，在下采样的[128,128]图像中将ground truth point以 的形式，用一个高斯核 
来将关键点分布到特征图上，其中 
是一个与目标大小(也就是w和h)相关的标准差。如果某一个类的两个高斯分布发生了重叠，直接去元素间最大的就可以。
这么说可能不是很好理解，那么直接看一个官方源码中生成的一个高斯分布[9,9]：
每个点 的范围是0-1,而1则代表这个目标的中心点，也就是我们要预测要学习的点。
损失函数的设计：
损失函数由三部分组成，分类损失，框的尺寸损失和中心点偏置损失
Lk为：
中 
和
是Focal Loss的超参数,N是图像 I 的的关键点数量，用于将所有的positive focal loss标准化为1。在这篇论文中和分别是2和4。这个损失函数是Focal Loss的修改版，适用于CenterNet。
这个损失也比较关键，需要重点说一下。和Focal Loss类似，对于easy example的中心点，适当减少其训练比重也就是loss值，当
的时候，
就充当了矫正的作用，假如 
接近1的话，说明这个是一个比较容易检测出来的点，那么 就相应比较低了。而当 接近0的时候，说明这个中心点还没有学习到，所以要加大其训练的比重，因此 就会很大,是超参数，这里取2。
高斯生成的中心点
再说下另一种情况，当 otherwise 的时候，这里对实际中心点的其他近邻点的训练比重(loss)也进行了调整，首先可以看到 
，因为当 otherwise 的时候 的预测值理应是0，如果不为0的且越来越接近1的话， 的值就会变大从而使这个损失的训练比重也加大；而 
则对中心点周围的，和中心点靠得越近的点也做出了调整(因为与实际中心点靠的越近的点可能会影响干扰到实际中心点，造成误检测)，因为
在上文中已经提到，是一个高斯核生成的中心点，在中心点 ，但是在中心点周围扩散 会由1慢慢变小但是并不是直接为0，类似于上图，因此 ，与中心点距离越近， 越接近1，这个值越小，相反则越大。那么 和 是怎么协同工作的呢？
简单分为几种情况：
- 对于距离实际中心点近的点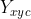， 值接近1，例如
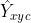，但是预测出来这个点的值 比较接近1，这个显然是不对的，它应该检测到为0，因此用 惩罚一下，使其LOSS比重加大些；但是因为这个检测到的点距离实际的中心点很近了，检测到的 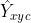接近1也情有可原，那么我们就同情一下，用 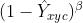来安慰下，使其LOSS比重减少些。
- 对于距离实际中心点远的点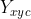， 值接近0，例如
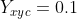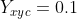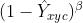，如果预测出来这个点的值 比较接近1，肯定不对，需要用 惩罚(原理同上)，如果预测出来的接近0，那么差不多了，拿 来安慰下，使其损失比重小一点；至于 的话，因为此时预测距离中心点较远的点，所以这一项使距离中心点越远的点的损失比重占的越大，而越近的点损失比重则越小，这相当于弱化了实际中心点周围的其他负样本的损失比重，相当于处理正负样本的不平衡了。 - 如果结合上面两种情况，那就是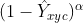： 和 来限制easy example导致的gradient被easy example dominant的问题，而 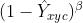则用来处理正负样本的不平衡问题(因为每一个物体只有一个实际中心点，其余的都是负样本，但是负样本相较于一个中心点显得有很多)。
目标中心的偏置损失
因为上文中对图像进行了 
的下采样，这样的特征图重新映射到原始图像上的时候会带来精度误差，因此对于每一个中心点，额外采用了一个local offset:
去补偿它。所有类 c的中心点共享同一个offset prediction，这个偏置值(offset)用L1 loss来训练：
采用L1 loss，设计这个损失的原因是因为，图像下采样时，GT的关键点会因数据是离散的而产生偏差，对每个中心点附加预测了个局部偏移，所有类别 c 共享同个偏移预测
上述公式直接看可能不是特别容易懂，其实 
是原始图像经过下采样得到的，对于[512,512]的图像如果的话那么下采样后就是[128,128]的图像，下采样之后对标签图像用高斯分布来在图像上撒热点，怎么撒呢？首先将box坐标也转化为与[128,128]大小图像匹配的形式，但是因为我们原始的annotation是浮点数的形式(COCO数据集)，使用转化后的box计算出来的中心点也是浮点型的，假设计算出来的中心点是[98.97667,2.3566666]。
但是在推断过程中，我们首先读入图像[640,320]，然后变形成[512,512]，然后下采样4倍成[128,128]。最终预测使用的图像大小是[128,128]，而每个预测出来的热点中心(headmap center)，假设我们预测出与实际标记的中心点[98.97667,2.3566666]对应的点是[98,2]，坐标是 (x,y)，对应的类别是 c，等同于这个点上 
，有物体存在，但是我们标记出的点是[98,2]，直接映射为[512,512]的形式肯定会有精度损失，为了解决这个就引入了 
偏置损失。
这个式子中 
是我们预测出来的偏置，而 
则是在训练过程中提前计算出来的数值，在官方代码中为：
# ct 即 center point reg是偏置回归数组，存放每个中心店的偏置值 k是当前图中第k个目标
reg[k] = ct - ct_int
# 实际例子为
# [98.97667 2.3566666] - [98 2] = [0.97667, 0.3566666]reg[k]之后与预测出来的reg一并放入损失函数中进行计算。注意上述仅仅是对某一个关键点位置
来计算的，计算当前这个点的损失值的时候其余点都是被忽略掉的。
到了这里我们可以发现，这个偏置损失是可选的，我们不使用它也可以，只不过精度会下降一些
目标大小的损失
我们假设
为目标k，所属类别为
，它的中心点为 
。我们使用关键点预测 
去预测所有的中心点。然后对每个目标k的size进行回归，最终回归到
，这个值是在训练前提前计算出来的，是进行了下采样之后的长宽值。
为了减少回归的难度，这里使用
作为预测值，使用L1损失函数，与之前的损失一样：
整体的损失函数为物体损失、大小损失与偏置损失的和，每个损失都有相应的权重。
在论文中 
，然后 
，论文中所使用的backbone都有三个head layer，分别产生[1,80,128,128]、[1,2,128,128]、[1,2,128,128]，也就是每个坐标点产生 C+4个数据，分别是类别以及、长宽、以及偏置。
推断阶段
在预测阶段，首先针对一张图像进行下采样，随后对下采样后的图像进行预测，对于每个类在下采样的特征图中预测中心点，然后将输出图中的每个类的热点单独地提取出来。具体怎么提取呢？就是检测当前热点的值是否比周围的八个近邻点(八方位)都大(或者等于)，然后取100个这样的点，采用的方式是一个3x3的MaxPool，类似于anchor-based检测中nms的效果。
这里假设 
为检测到的点，
代表c 类中检测到的一个点。每个关键点的位置用整型坐标表示 
，然后使用 
表示当前点的confidence，随后使用坐标来产生标定框：
其中 
是当前点对应原始图像的偏置点， 
代表预测出来当前点对应目标的长宽。
下图展示网络模型预测出来的中心点、中心点偏置以及该点对应目标的长宽：
那最终是怎么选择的，最终是根据模型预测出来的 ![\hat{Y}\varepsilon [0,1]]^{\frac{W}{R}\times \frac{H}{R}\times C}](http://img.e-com-net.com/image/info8/e49147fc7bcf44d7a4d62624fb299c94.gif){kind=small}
值，也就是当前中心点存在物体的概率值，代码中设置的阈值为0.3，也就是从上面选出的100个结果中调出大于该阈值的中心点作为最终的结果。
例子
运行官方源码的demo，随便挑了一张图，跑出来的结果分别对应最终图，取top=100的检测图以及预测出来的heatmap。
最终效果图
top=100的检测图
预测出来的heatmap
后记
总之这是一篇笔记，好久没有认真阅读一篇论文了。搞工程搞多了看见论文就头大，但是好的论文还是值得一读了，特别是这一篇。这篇论文厉害的地方在于：
- 设计模型的结构比较简单，像我这么头脑愚笨的人也可以轻松看明白，不仅对于two-stage，对于one-stage的目标检测算法来说该网络的模型设计也是优雅简单的。
- 该模型的思想不仅可以用于目标检测，还可以用于3D检测和人体姿态识别，虽然论文中没有是深入探讨这个，但是可以说明这个网络的设计还是很好的，我们可以借助这个框架去做一些其他的任务。
- 虽然目前尚未尝试轻量级的模型(这是我接下来要做的！)，但是可以猜到这个模型对于嵌入式端这种算力比较小的平台还是很有优势的，希望大家多多尝试一些新的backbone(不知道mobilenetv3+CenterNet会是什么样的效果)，测试一下，欢迎和我交流呀~
当然说了一堆优点，CenterNet的缺点也是有的，那就是：
- 在实际训练中，如果在图像中，同一个类别中的某些物体的GT中心点，在下采样时会挤到一块，也就是两个物体在GT中的中心点重叠了，CenterNet对于这种情况也是无能为力的，也就是将这两个物体的当成一个物体来训练(因为只有一个中心点)。同理，在预测过程中，如果两个同类的物体在下采样后的中心点也重叠了，那么CenterNet也是只能检测出一个中心点，不过CenterNet对于这种情况的处理要比faster-rcnn强一些的，具体指标可以查看论文相关部分。
- 有一个需要注意的点，CenterNet在训练过程中，如果同一个类的不同物体的高斯分布点互相有重叠，那么则在重叠的范围内选取较大的高斯点。