八数码问题

八数码问题

八数码问题也叫九宫问题，是人工智能中状态搜索中的经典问题，其中，该问题描述为：在3×3的棋盘，摆有八个棋子，每个棋子上标有1至8的某一数字，不同棋子上标的数字不相同。棋盘上还有一个空格，与空格相邻的棋子可以移到空格中。要求解决的问题是：给出一个初始状态和一个目标状态，找出一种从初始转变成目标状态的移动棋子步数最少的移动步骤。

这是一个典型的图搜索问题，但是该问题并不需要正在建立图数据结构来进行求解，而是将图的搜索方法抽象，运用到该问题上。以下是分析过程：

首先考虑将算法问题进行抽象和编码。如果把空格记成0，棋盘上的所有状态共有 9! =
362880种。我们要先找到一种方法把棋盘的状态进行编码。

容易想到的直观的状态表示方法，采用字符串方式编码，即把3*3的九宫格展平为一个长度为9的串，这样一个串即可代表一种当前整个数码盘的状态，例如：状态123456780表示如下：

1	2	3
4	5	6
7	8	0

进一步的，考虑转移（改变）状态，因为考虑只能由空格和一个数字进行对换，因此即可从数字0的位置开始考虑状态的转移，例如：上述的状态能够进行两种方向的转移，即为0和8进行对换，0和6进行对换，图示如下：

1	2	3
4	5	0
7	8	6

向上方式的转移

1	2	3
4	5	6
7	0	8

向左方向的转移

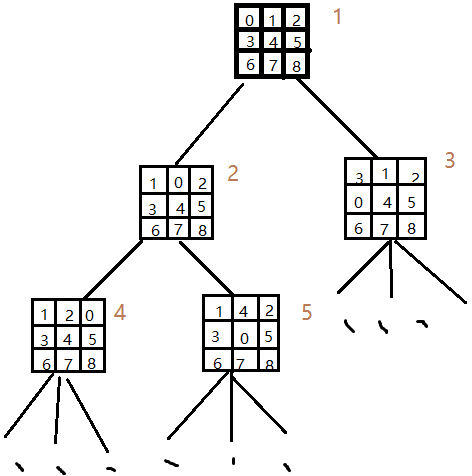
这样就可以从初始的状态扩展为一颗向目标状态的状态搜索树如下：

图片 1 状态搜索树

不难看出，一颗搜索树的深度，即为当前空格所对换的次数。

算法分析

暴力枚举状态

若把空格记为0，那么状态的总数应该是0到9的排列数，即为9！=362,880‬个状态，使用的算法为二进制枚举，即枚举所有排列中满足当前的状态符合转移要求的那一部分，每一次枚举下一个状态是否可行，这样的算法是及其低效的、甚至是无法在有限时间内求解。

深度优先搜索

进一步思考，转移状态的条件开始考虑，移动其他数字与0替换位置等效于移动0与其周围的位置进行替换，因此，每次转移状态即可从0的位置考虑。这样就确定了搜索的思路，进一步划分，搜索又可分为深度优秀搜索和广度优先搜索。

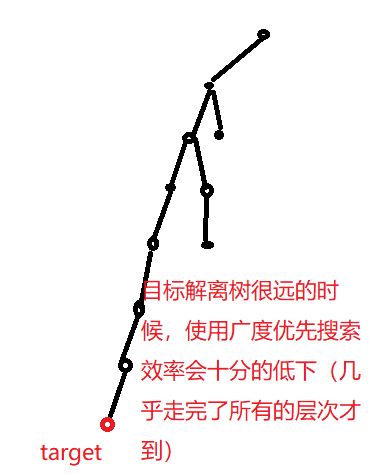
对于深度优先搜索，即为将“当前的路子一脑子走到底”，直到当前的状态符合搜索要求，或者已经无法继续扩展为新的状态时暂停。这样的搜索容易在某一较深的分支上停留很长时间，对于目标分布远离初始的搜索方向的搜索树来说，效率是极低的。搜索状态图扩展的搜索树如下图：

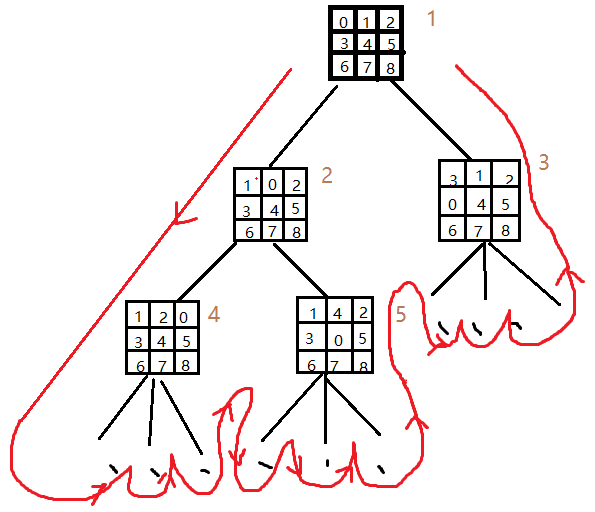
图片 2广度优先搜索路径

对于该例来说：广度优先搜索的路径可以用文字描述为：

根节点状态（起始状态1）

1. 访问当前的最左的未访问过的节点（到节点2），并且节点不是目标状态。

2. 访问当前的最左的未访问过的节点（到节点4），并且节点不是目标状态。

3. 访问当前的最左的未访问过的节点（到节点4的子树部分），并且节点不是目标状态。

4. 当前节点无可扩展节点，回溯（回到节点4）

5. 当前节点无可扩展节点，回溯（回到节点2）

6. 访问当前的最左的未访问过的节点（到节点5），并且节点不是目标状态。

7. …（以此类推）

8. 当前节点是目标节点，搜索结束，并且输出当前搜索树深度。

9. 否则，一直拓展并且回溯到根节点，搜索不到目标状态，退出搜索。

这样，很清晰的看出，假设搜索是优先搜索左子树，当目标状态（解）在最右边子树的最右子节点时，搜索效率是十分低效的，搜索的次数约等于排列数9！=362,880。而若目标状态位于最左子树的最左节点，那么搜索将是常数级别的，即一股脑走到树的叶子节点即可输出最优解。

伪代码可以描述如下：

首先将根节点放入stack中。

1. 从stack中取出第一个节点，并检验它是否为目标。

如果找到目标，则结束搜寻并回传结果。

否则将它某一个尚未检验过的直接子节点加入stack中。

1. 重复步骤2。

2. 如果不存在未检测过的直接子节点。

将上一级节点加入stack中。

重复步骤2。

1. 重复步骤4。

2. 若stack为空，表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。

因此，综上来说，深度优先搜索改进了暴力枚举状态的算法，使得时间在可以接受的时间内求出，但是依旧有一定问题，例如：

1. 搜索时间不稳定。搜索的时间依赖于目标状态的分布，若运气较好，目标状态和初始搜索方向相近并且在树上分布较浅，那么就可以快速得到解，若运气较差，需要一直回溯，直到到达目标状态所在的子树，这样的效率约等于硬枚举排列数，搜索空间是十分巨大的。

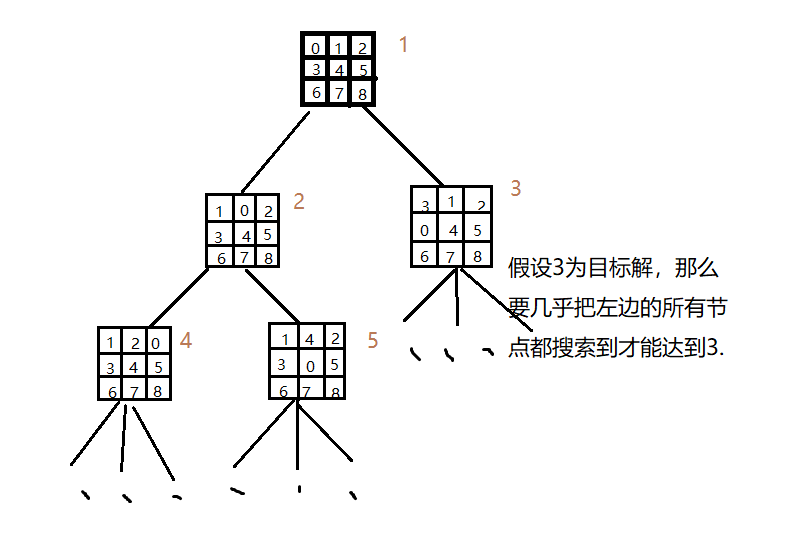
2. 算法较为蛮力。仔细分析，对于树的每一个分支来说，搜索到目标状态的概率是一定不同的，而这些概率是可以作为搜索时的信息来进行一定的优化，而深度优先搜索则是对每一条分支都等价的认为其搜索到目标状态的概率是相同的，这明显是不合理的、缺乏优化的。

图片 3 深度优先搜索的不足

广度优先搜索

广度优先搜索是搜索策略中另外一大分支，思路不再是“一股脑走到底”,而是“泛的扩展”。这样，在同一个深度下分布在搜索树上右边的目标节点和分布在搜索树左边的节点在搜索的次数上是大致相同的。

同样使用上述的图例进行说明：

可以看出,节点从根部节点开始扩展,首先访问的是根节点的子节点们,然后从子节点们扩展到下一层的子节点们,即扩展是有层次关系的。这样，对于层次位于叶子节点附近的集合,就能有公平的概率搜索到。上图中的节点访问顺序就是先访问层次1的所有节点,随后是层次2的所有节点，直到搜索到目标解，或者无法继续扩展而结束。这样，对于广度优先搜索中，每一次扩展都是搜索当前状态可以拓展的下一次状态，即搜索的是树中的每一层。

伪代码可以描述如下：

队列Q；visited[n]=0；

1. 访问顶点v；visited[v]=1；顶点v入队列Q；

2. while（队列Q非空）   
                 v=队列Q的对头元素出队；
                 w=顶点v的第一个邻接点；
                while（w存在） 
                        如果w未访问，则访问顶点w；
                        visited[w]=1；
                        顶点w入队列Q；
                        w=顶点v的下一个邻接点。

同样，深度优先搜索也是一种蛮力搜索的算法，缺点表现如下：

1. 无差别的搜索，和深度优先搜索一样，广度优先搜索也是一种无差别的等概率的选择搜索的分支，而广度优先搜索在树的左右极度的不平衡时，会导致搜索的效率极低。但是在本问题中，由于扩展的方向只有上下左右四种情况，因此，扩展的分支是较为平衡的。树不会倾斜与某一边。所以，广度优先搜索是在该问题上是好于深度优先搜索的。

2. 空间消耗巨大,广度优先搜索需要同时维护两张表,close表和open表的空间开销都是巨大的。

附带哈希表的广度优先搜索

上一个算法很好的解决了深度优先搜索一股脑的走到底的问题，并且分析了在八数码问题上两者的区别。虽然，广度优先搜索已经能够在有限并且可以接受的时间内进行求解，但是必然是很粗糙的求解方法，有很多待优化的地方。

首先，对于每次扩展时，应该找到当前未访问过的节点，这其中就涉及到查重操作，而之前的广度优先方法是使用map数据结构进行查重的，这种数据结构的查询的效率是对数级别的，但是对于空间内每一次拓展都需要查询，开销在时间和空间上的积累就会很高。

为了解决这个问题，需要考虑一个查询效率极高的数据结构，哈希表就是这样的一种数据结构。它可以使得查询的时间复杂度降到常数级别，并且对于存储空间来说，若哈希函数设计合理，也可以近似地看作是线性的增长率损耗。

哈希部分的算法可以描述为：

插入元素:

计算插入元素的哈希值

查看是否有哈希冲突

emsp;有冲突，进行跳转，直到能插入。
emsp;无冲突，插入元素。

删除元素：
计算哈希值

查看当前的位置是否是待删除的元素。

emsp;是，删除元素

emsp;否，进行计算哈希跳转，知道找到删除元素的位置。

双向广度优先搜索

前面对于广度优先搜索算法的描述已经很详细了，这里对其进一步扩展。讨论一种更加高效的算法。

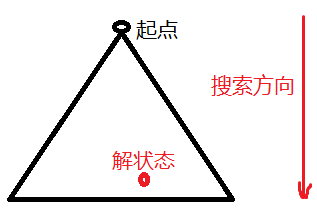
对于广度优先搜索，只能从一个方向进行搜索，即为从初始的状态到目标状态方向搜索，即整个搜索路径可以看作一个三角形扩展的过程。

如图：

图片 4 bfs的搜索方向

而上文中提到过，如果目标节点位于接近叶子节点的位置时，那么从起点位置开始广度优先搜索效率会十分的低下。

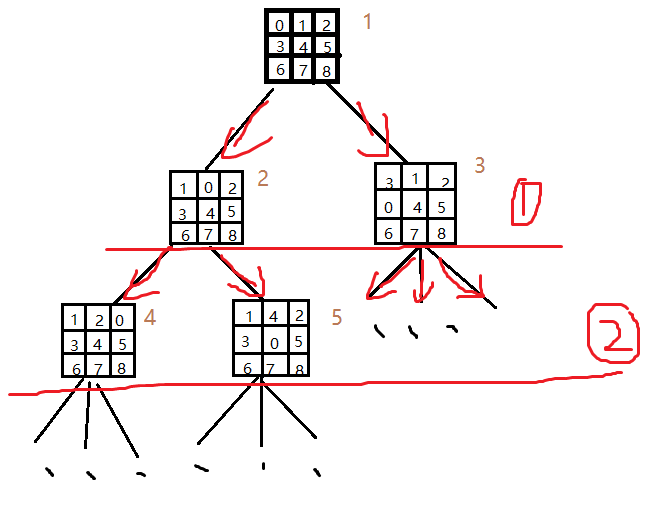
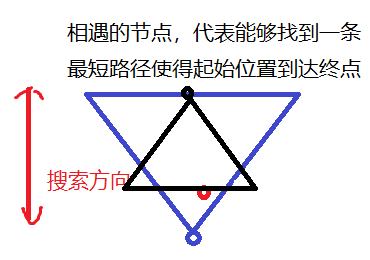
那么，我们可不可以考虑，从目标方向也开始搜索，在目标状态开始扩展的树与初始状态开始扩展的树的节点相遇时，表示搜索得到了的目标。这便是双向深度优先搜索算法，这样如果解离叶子节点很接近，自底向上的搜索支路能够很快的和自顶向下的支路汇合，可以有效的解决解接近于根节点而导致的低效问题。

图片 5 从两边扩展的双向广度优先搜索

同时从两边扩展，加入到open表内，进行搜索。

启发式算法A*

在前文讨论过，使用无差别的搜索是不太合理的，因为每一条搜索路线上找到解的几率都不一样。因此，需要找到一种能够找到算法，使得在能够最大可能搜索到解的路线上进行优先的搜索。A*搜索算法就是在深度优先搜索中加入了这样叫做估价函数的机制，使得能够优先选择有大概率搜索到可能的支路。

其中的估价函数就是对当前支路下可能搜索到目标的概率估计。

在主循环的每次迭代中，A
*需要确定要扩展的路径。它基于路径的成本以及将路径一直扩展到目标所需的成本估算值来进行操作。具体来说，A
*选择最小化的路径

{\ displaystyle f（n）= g（n）+ h（n）}

图片 6 估价函数

其中n是路径上的下一个节点，g（n）是从起始节点到n的路径的成本，h（n）是一种启发式函数，用于估计从n到目标的最便宜路径的成本。

这样，在估价函数的作用下，搜索路线会合理的选择一条由估价函数决定的当前情况较为合理的路线。

在查阅了一定资料后，发现在设计估价函数时，应该使其动态变化，
一般准则引子百度百科：

图片 7 估价函数的设计准则