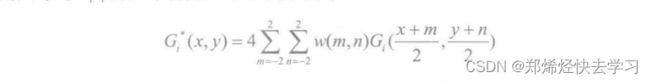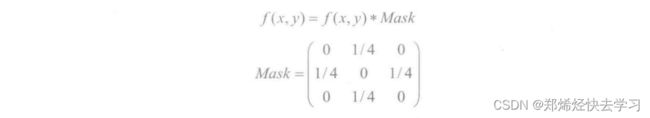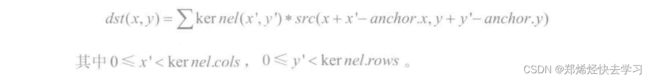OpenCV入门(十一)——图像平滑技术
关于图像采样
数字图像的获取途径有很多方式,通常可利用图像采样在连续图像上进行数字化。采样点之间形成的集合关系就是栅格,栅格间无限小的采样点对应于图像中的像素点。图像变换上的采样就是将图像分辨率改变的过程,采样分为上采样和下采样。
上采样为:指将图分辨率扩大。
下采样为:图像的分辨率缩小。
目录
0x01 最近邻插值
0x02 双线性插值
0x03 图像金字塔
0x04 傅里叶变换
OPenCV常见的图像缩放有两种方式:
-
几何变换中提供的resize函数。
-
基于分辨率理论的图像金字塔pyrDown与pyrUp。
0x01 最近邻插值
最近邻插值是最简单的图像处理的方法,其原理是提取源数据图像中与其邻域最近像素值来作为目标图像相对应点的像素值。源图像f(x,y)的分辨率为w*h,进行缩放后目标图像为f(x',y')的分辨率为w’ * h‘,那么最近邻插值变换如下:
最近邻插值缩放最关键的步骤是找到缩放倍数。然后邻域向上取整完成坐标映射。OpenCV中提供了个将浮点数转换为整数的函数 ,具体是:cvRound函数返回和参数最接近的整数值,四舍五入。cvFloor返回不大于参数的最大整数值;cvCeil返回不小于参数的最小整数值。
那么我们就试着使用最近邻插值来实现,其实这个用法一直广泛使用于在单片机中的图像的缩放:
其实这个算法说的通俗点就是,我们把缩放系数算出来,之后按照缩放的系数N我们可以得出,我们将N个源图像的像素点视为一个点。
代码如下:
#include
#include
#include
#include
#include "opencv2/core/core.hpp"
#include "opencv2/core/utility.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/imgcodecs.hpp"
#include "opencv2/highgui/highgui.hpp"
#include
#include
using namespace cv;
using namespace std;
// 实现最近邻插值图像缩放
cv::Mat nNeighbourInterpolation(cv::Mat srcImage)
{
// 判断输入有效性
CV_Assert(srcImage.data != NULL);
int rows = srcImage.rows;
int cols = srcImage.cols;
// 构建目标图像
cv::Mat dstImage = cv::Mat(
cv::Size(rows/2, cols/2), srcImage.type(),
cv::Scalar::all(0));
int dstRows = dstImage.rows;
int dstCols = dstImage.cols;
// 坐标转换 求取缩放倍数
float cx = (float)cols / dstCols;
float ry = (float)rows / dstRows;
std::cout << "cx: " << cx << "ry:" << ry << std::endl;
// 遍历图像完成缩放操作
for (int i = 0; i < dstCols; i++)
{
// 取整获取目标图像在源图像对应坐标
int ix = cvFloor(i * cx);
for (int j = 0; j < dstRows; j++)
{
int jy = cvFloor(j * ry);
// 边界处理 防止指针越界
if (ix > cols - 1)
ix = cols - 1;
if (jy > rows - 1)
jy = rows - 1;
// 映射矩阵
dstImage.at(j, i) =
srcImage.at(jy, ix);
}
}
return dstImage;
}
int main()
{
// 图像源获取及验证
cv::Mat srcImage = cv::imread("./image/AA.png");
if (!srcImage.data)
return -1;
// 最近邻插值缩放操作
cv::Mat dstImage = nNeighbourInterpolation(srcImage);
cv::imshow("srcImage", srcImage);
cv::imshow("dstImage", dstImage);
cv::waitKey(0);
return 0;
} 0x02 双线性插值
双线性插值处理是应用最广泛的图像缩放方法之一,其稳定性高且时间复杂度较优。双线性插值的原理是通过计算源数据图像的位置点邻域(2*2)像素值的加权平均,进而得到目标图像相对应的位置点。
实现的话可以通过寻找距离这个对应坐标点最近的四个相邻坐标点来计算对应坐标,计算公式如下:
其中yk为距离最近的四个相邻点,wk为对应点相应的权重比例。需要注意的是,双线性插值中涉及的大部分都是浮点型数据的运算,对坐标转换应考虑优化,常见的优化是改变映射关系:((i+0.5) * w/w'-0.5,(j+0.5)*h/h'-0.5)。双线性插值利用区域邻域的特征使得变换后的图像像素值连续,一定程度上弱化了高频分量信息,图像轮廓将出现一定程度上的模糊。
那么实现的函数如下:
cv::Mat BilinearInterpolation(cv::Mat srcImage)
{
CV_Assert(srcImage.data != NULL);
int srcRows = srcImage.rows;
int srcCols = srcImage.cols;
int srcStep = srcImage.step;
// 构建目标图像
cv::Mat dstImage = cv::Mat(
cv::Size(150, 150), srcImage.type(),
cv::Scalar::all(0));
int dstRows = dstImage.rows;
int dstCols = dstImage.cols;
int dstStep = dstImage.step;
// 数据定义及转换
IplImage src = cvIplImage(srcImage);
IplImage dst = cvIplImage(dstImage);
std::cout << "srcCols:" << srcCols << " srcRows:" <<
srcRows << "srcStep:" << srcStep << std::endl;
std::cout << "dstCols:" << dstCols << " dstRows:" <<
dstRows << "dstStep:" << dstStep << std::endl;
// 坐标定义
float srcX = 0, srcY = 0;
float t1X = 0, t1Y = 0, t1Z = 0;
float t2X = 0, t2Y = 0, t2Z = 0;
for (int j = 0; j < dstRows - 1; j++)
{
for (int i = 0; i < dstCols - 1; i++)
{
// 缩放映射关系
srcX = (i + 0.5) * ((float)srcCols) / (dstCols)-0.5;
srcY = (j + 0.5) * ((float)srcRows) / (dstRows)-0.5;
int iSrcX = (int)srcX;
int iSrcY = (int)srcY;
// 三通道求邻域加权值1
t1X = ((uchar*)(src.imageData + srcStep * iSrcY))[
iSrcX * 3 + 0] * (1 - std::abs(srcX - iSrcX)) +
((uchar*)(src.imageData + srcStep * iSrcY))[
(iSrcX + 1) * 3 + 0] * (srcX - iSrcX);
t1Y = ((uchar*)(src.imageData + srcStep * iSrcY))[
iSrcX * 3 + 1] * (1 - std::abs(srcX - iSrcX)) +
((uchar*)(src.imageData + srcStep * iSrcY))[
(iSrcX + 1) * 3 + 1] * (srcX - iSrcX);
t1Z = ((uchar*)(src.imageData + srcStep * iSrcY))[
iSrcX * 3 + 2] * (1 - std::abs(srcX - iSrcX)) +
((uchar*)(src.imageData + srcStep * iSrcY))[
(iSrcX + 1) * 3 + 2] * (srcX - iSrcX);
// 三通道求邻域加权值2
t2X = ((uchar*)(src.imageData + srcStep * (
iSrcY + 1)))[iSrcX * 3] * (1 - std::abs(srcX - iSrcX))
+ ((uchar*)(src.imageData + srcStep * (
iSrcY + 1)))[(iSrcX + 1) * 3] * (srcX - iSrcX);
t2Y = ((uchar*)(src.imageData + srcStep * (
iSrcY + 1)))[iSrcX * 3 + 1] * (1 - std::abs(srcX - iSrcX))
+ ((uchar*)(src.imageData + srcStep * (
iSrcY + 1)))[(iSrcX + 1) * 3 + 1] * (srcX - iSrcX);
t2Z = ((uchar*)(src.imageData + srcStep * (
iSrcY + 1)))[iSrcX * 3 + 2] * (1 - std::abs(srcX - iSrcX))
+ ((uchar*)(src.imageData + srcStep * (iSrcY + 1)))[(
iSrcX + 1) * 3 + 2] * (srcX - iSrcX);
// 根据公式求解目标图像加权
((uchar*)(dst.imageData + dstStep * j))[i * 3] =
t1X * (1 - std::abs(srcY - iSrcY)) + t2X * (
std::abs(srcY - iSrcY));
((uchar*)(dst.imageData + dstStep * j))[i * 3 + 1] =
t1Y * (1 - std::abs(srcY - iSrcY)) + t2Y * (
std::abs(srcY - iSrcY));
((uchar*)(dst.imageData + dstStep * j))[i * 3 + 2] =
t1Z * (1 - std::abs(srcY - iSrcY)) + t2Z * (
std::abs(srcY - iSrcY));
}
// 列操作
((uchar*)(dst.imageData + dstStep * j))[(dstCols - 1) * 3] =
((uchar*)(dst.imageData + dstStep * j))[(dstCols - 2) * 3];
((uchar*)(dst.imageData + dstStep * j))[(dstCols - 1) * 3 +
1] = ((uchar*)(dst.imageData + dstStep * j))[(
dstCols - 2) * 3 + 1];
((uchar*)(dst.imageData + dstStep * j))[(dstCols - 1) * 3
+ 2] = ((uchar*)(dst.imageData + dstStep * j))[(
dstCols - 2) * 3 + 2];
}
// 行操作
for (int i = 0; i < dstCols * 3; i++)
{
((uchar*)(dst.imageData + dstStep * (dstRows - 1)))[i] =
((uchar*)(dst.imageData + dstStep * (dstRows - 2)))[i];
}
return dstImage;
}
int main()
{
cv::Mat srcImage = cv::imread("./image/BB.png");
if (!srcImage.data)
return -1;
cv::Mat dstImage = BilinearInterpolation(srcImage);
cv::imshow("srcImage", srcImage);
cv::imshow("dstImage", dstImage);
cv::waitKey(0);
return 0;
}OpenCV中提供的resize函数可以实现图像大小的变换,默认插值方法为双线性插值。那么他们三种方法之间哪种效率比较高?resize函数中双线性插值与最近邻插值的时间复杂度相对较低。线性插值为较优。
0x03 图像金字塔
图像金字塔是一系列图像的集合。所有多个分辨率的图像来源于同一原始图像,常用于图像缩放或图像分割中。图像金字塔结构是用于多分辨率处理的一种图像存储数据结构,向下采样技术是高斯金字塔,向上重建技术是拉普拉斯金字塔。
(一)高斯金字塔
高斯金字塔的生成过程包含高斯核卷积和下采样过程,设源图像为G0(x,y),分辨率为M*N,G0表示高斯金字塔的最底层为第0层,即与源图像相同。未得到高斯金字塔层数Gi+1图像,首先对源图像Gi进行高斯内核卷积,然后删除所有偶数行和偶数列。那么常见的高斯核函数取值如下:
高斯金字塔向下减少的方式如下式所示:
对于层级i,Gi=Reduce[Gi-1],w(m,n)为生成核,窗口函数是一个低通滤波器,上述对生成核的限制是为了既能保证低通的性质,又能保证图像缩扩后的亮度平滑,不出现边界缝隙。
通过上式可知,图像金字塔是对下一层进行低通滤波后再进行隔行列采样得到的,当前层图像的大小依次为前一层的图像大小的1/4。
(二)拉普拉斯金字塔
拉普拉斯金字塔操作实现向上重建图像,上面的高斯是一直在向下缩小图像,而拉普拉斯金字塔是相反的。
对Gi内插得到放大图像Gi*,使Gi *的尺寸与Gi-1的尺寸相同,可表达为下式:
其中i的取值范围为(0,N),x的取值范围为[0,M),y的取值范围为[0,N)。对于上式中的Gi*((x+m)/2,(y+n)/2),当且(x+m)/2与(y+n)/2为整数时可变换为Gi((x+m)/2,(y+n)/2),其他情况下为0。
书里对这条公式的解释为:
OpenCV中对图像金字塔的实现提供了pyrUp和pyrDoen函数用于向上和向下采样。
void pyrDown( InputArray src,
OutputArray dst,
const Size& dstsize = Size(), //输出图像大小
int borderType = BORDER_DEFAULT );
void pyrUp( InputArray src,
OutputArray dst,
const Size& dstsize = Size(),
int borderType = BORDER_DEFAULT );-
dstsize:表示输出图像大小,Size((src.cols+1)/2,(src.rows+1)/2)为默认值。那么默认参数的条件下要满足:pyrDown:|dstsize.width*2-src.cols|<=2及|dstsize.height * 2-src.rows|<=2。pyrUp:|dstsize.width-src.cols * 2|<=(dstsize.width mod 2),|dstsize.height- src.rows * 2|<=(dstsize.height mod 2)
那么通过代码来看看效果吧:
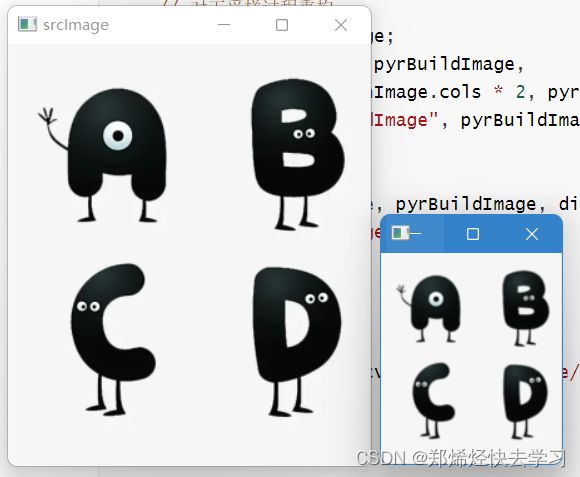
我们使用下面这幅图来做实验:
先看看代码:
#include
#include
#include
#include
#include "opencv2/core/core.hpp"
#include "opencv2/core/utility.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/imgcodecs.hpp"
#include "opencv2/highgui/highgui.hpp"
#include
#include
// 图像金子塔采样操作
void Pyramid(cv::Mat srcImage)
{
// 根据图像源尺寸判断是否需要缩放
if (srcImage.rows > 400 && srcImage.cols > 400)
cv::resize(srcImage, srcImage, cv::Size(), 0.5, 0.5);
else
cv::resize(srcImage, srcImage, cv::Size(), 1, 1);
cv::imshow("srcImage", srcImage);
cv::Mat pyrDownImage, pyrUpImage;
// 下采样过程
pyrDown(srcImage, pyrDownImage,
cv::Size(srcImage.cols / 2, srcImage.rows / 2));
cv::imshow("pyrDown", pyrDownImage);
// 上采样过程
pyrUp(srcImage, pyrUpImage,
cv::Size(srcImage.cols * 2, srcImage.rows * 2));
cv::imshow("pyrUp", pyrUpImage);
// 对下采样过程重构
cv::Mat pyrBuildImage;
pyrUp(pyrDownImage, pyrBuildImage,
cv::Size(pyrDownImage.cols * 2, pyrDownImage.rows * 2));
cv::imshow("pyrBuildImage", pyrBuildImage);
// 比较重构性能
cv::Mat diffImage;
cv::absdiff(srcImage, pyrBuildImage, diffImage);
cv::imshow("diffImage", diffImage);
cv::waitKey(0);
}
int main()
{
cv::Mat srcImage = cv::imread("./image/BB.png");
if (!srcImage.data)
return -1;
Pyramid(srcImage);
return 0;
} 这个函数首先分析了上采用以及下采样,之后再对下采样的过程进行重构,也就是将其放大,之后再比较重构后的图像与原来的图像有什么区别:
那么首先对比下采样图像:
我们可以发现下采样的图片边得非常模糊。
那么再对比上采用图像:
我们也可以发现放大后的图片也变得有些模糊。
之后我们试着将下采样的图片进行重构,我们将其放大两倍,使用源图像以及下采样图像和重构图像进行对比:
这也太模糊了吧。。。跟近视眼效果差不多。。。
之后再看看源图像以及重构后的图像作差,看看之间的区别在哪:
那么惊喜的发现这个东西可以画出轮廓。。怎么说呢。。我觉得适合对于模糊图像的处理吧。
确实也可以滤掉一部分的锯齿。效果还是挺满意的。
0x04 傅里叶变换
(一)图像掩码操作
图像的掩码操作是指通过掩码核算子重新计算图像中各个像素的值,掩码核算子刻画邻域像素点对新像素值的影响程度,同时根据掩码算子刻画邻域像素点对新像素值的影响操作,同时根据掩码算子中权重因子对原像素点进行加权平均。
图像掩码操作通常哟关于图像平滑、边缘检测及特征分析等领域。OpenCV中常用的计算图像掩码的操作有如下两种:
(1)基于像素邻域遍历
对于源图像数据f(x,y),卷积核算子为3*3,计算源图像数据4邻域均值掩码可通过下式来完成:
基于像素邻域遍历就是通过对源数据矩阵进行操作,利用上面的公式以当前像素点为计算中心目标点,逐像素移动掩码核算子模板,对源图像数据进行遍历,进而更新新图像对应的每个像素点值。
(2)基于filter2D函数
OpenCV中提供了filter2D函数专门应用于计算机图像卷积操作的操作:
void filter2D( InputArray src,
OutputArray dst,
int ddepth, //输出图形深度
InputArray kernel, //卷积核算子
Point anchor = Point(-1,-1), //卷积核锚点
double delta = 0, //平滑技术
int borderType = BORDER_DEFAULT );-
ddepth:如果设置为负值,其深度与输入源数据深度一样,否则就需要根据输入源图像的深度进行相关设置。
若src.depth()=CV_8U,则ddepth=-1/CV_16S/CV_32F/CV_64F;
若src.depth()=CV_16U/CV_16S,则ddepth=-1/CV_32F/CV_64F;
若src.depth()=CV_32F,则ddepth=-1/CV_32F/CV_64F;
若src.depth()=CV_64F,则ddepth=-1/CV_64F。
-
参数kernel为卷积核算子,为单通道浮点矩阵,如果对多通道应用不同卷积核算子计算,需要分离通道然后对其进行单个操作。
-
参数anchor为卷积核锚点,默认为(-1,-1),表示卷积核中心。
-
参数delta,目前图像生成前可设定值用于平滑操作。
filter2D函数常用于线性滤波技术中,当使用卷积核算子计算的图像目标点在图像外部时,需要对指定边界进行插值运算。
该函数实际计算的是图像相关性,而不是卷积操作,filter2D的计算公式是:
那么以上的两种掩码操作的实现:
#include
#include
#include
#include
#include "opencv2/core/core.hpp"
#include "opencv2/core/utility.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/imgcodecs.hpp"
#include "opencv2/highgui/highgui.hpp"
#include
#include
using namespace cv;
using namespace std;
// 基于像素邻域掩码操作
cv::Mat Myfilter2D(cv::Mat srcImage)
{
const int nChannels = srcImage.channels();
cv::Mat resultImage(srcImage.size(), srcImage.type());
for (int j = 1; j < srcImage.rows - 1; ++j)
{
// 获取邻域指针
const uchar* previous = srcImage.ptr(j - 1);
const uchar* current = srcImage.ptr(j);
const uchar* next = srcImage.ptr(j + 1);
uchar* output = resultImage.ptr(j);
for (int i = nChannels; i < nChannels * (srcImage.cols - 1); ++i)
{
// 4-邻域均值掩码操作
*output++ = saturate_cast(
(current[i - nChannels] + current[i + nChannels] +
previous[i] + next[i]) / 4);
}
}
// 边界处理
resultImage.row(0).setTo(Scalar(0));
resultImage.row(resultImage.rows - 1).setTo(Scalar(0));
resultImage.col(0).setTo(Scalar(0));
resultImage.col(resultImage.cols - 1).setTo(Scalar(0));
return resultImage;
}
// 自带库掩码操作
cv::Mat filter2D_(cv::Mat srcImage)
{
cv::Mat resultImage(srcImage.size(), srcImage.type());
Mat kern = (Mat_(3, 3) << 0, 1, 0,
1, 0, 1,
0, 1, 0) / (float)(4);
filter2D(srcImage, resultImage, srcImage.depth(), kern);
return resultImage;
}
int main()
{
cv::Mat srcImage = cv::imread("./image/flower.png");
if (!srcImage.data)
return 0;
cv::Mat srcGray;
cvtColor(srcImage, srcGray, CV_BGR2GRAY);
imshow("srcGray", srcGray);
cv::Mat resultImage = Myfilter2D(srcGray);
imshow("resultImage", resultImage);
cv::Mat resultImage2 = filter2D_(srcGray);
imshow("resultImage2", resultImage2);
cv::waitKey(0);
return 0;
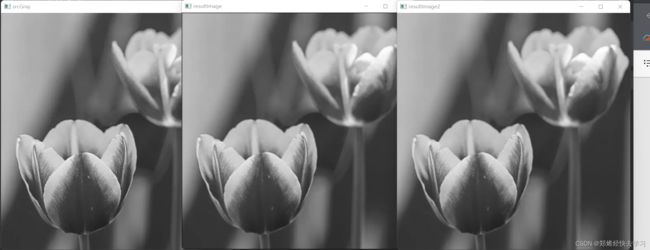
} 首先看看原先的灰度图像:
基于像素邻域掩码操作:
基于filter2D操作:
其实这么看好像看不出什么区别,那拼在一起:
其实我只是感觉到第三张使用filter2D处理的图像色调有些偏黄。。还是喜欢基于像素邻域掩码操作的效果。